Đề kiểm tra Tính đơn điệu và cực trị của hàm số (có lời giải) - Đề 4
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 24. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Cho hàm số \(y = {x^3} + 3x + 2\). Mệnh đề nào dưới đây là đúng?
Hàm số đồng biến trên khoảng \(\left( { - \infty ; + \infty } \right)\).
Hàm số nghịch biến trên khoảng \(\left( { - \infty ; + \infty } \right)\).
Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và đồng biến trên khoảng \(\left( {0; + \infty } \right)\).
Hàm số đồng biến trên khoảng \(\left( { - \infty ;0} \right)\) và nghịch biến trên khoảng \(\left( {0; + \infty } \right)\).
Cho hàm số \[y = \frac{{{x^3}}}{3} - 2{x^2} + 3x + \frac{2}{3}\]. Toạ độ điểm cực đại của đồ thị hàm số là
\[\left( { - 1;2} \right).\]
\(\left( {3;\frac{2}{3}} \right).\)
\[\left( {1; - 2} \right).\]
\[\left( {1;2} \right).\]
Biết đồ thị hàm số \(y = {x^3} + 3{x^2} - 9x - 1\) có hai cực trị \[A\] và \[B\]. Điểm nào dưới đây thuộc đường thẳng\[AB\]?
\[N\left( {0;\,2} \right)\].
\[P\left( { - 1;\,1} \right)\].
\[Q\left( { - 1;\, - 8} \right)\].
\[M\left( {0;\, - 1} \right)\].
Có bao nhiêu giá trị nguyên của tham số \(m \in \left[ { - 2024;2024} \right]\)để hàm số \(y = \sqrt {{x^2} + 1} - mx - 1\) đồng biến trên \(\mathbb{R}\).
\(2024\).
\(2019\).
\(2020\).
\(0\).
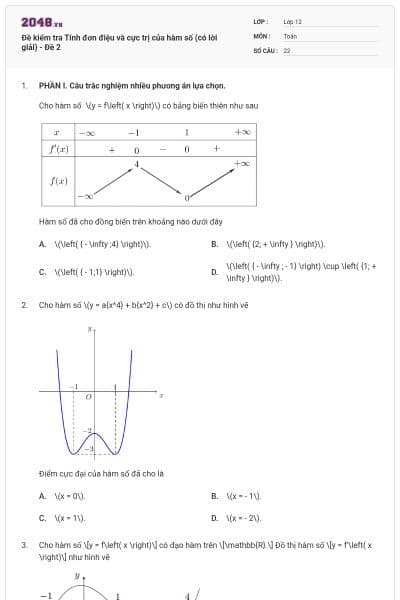
Cho hàm số \(y = f(x)\) có bảng biến thiên :
Hàm số đồng biến trên khoảng nào ?
\((1; + \infty ).\)
\[(1;2)\].
\[( - \infty ;2)\].
\[(2; + \infty )\].
Cho hàm số \(y = f(x)\) liên tục trên R và có bảng xét dấu của đạo hàm như hình vẽ.
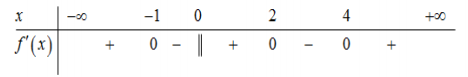
Hàm số đã cho có bao nhiêu điểm cực trị?
\(4\).
\(1\).
\(3\).
\(2\).
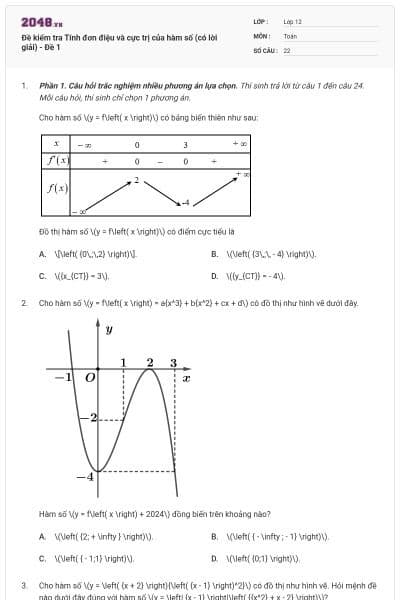
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
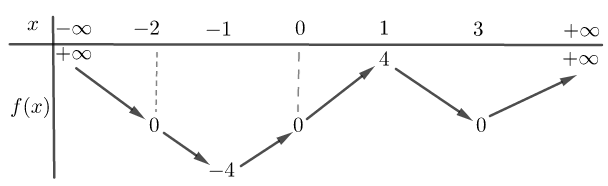
Hàm số \(g\left( x \right) = \frac{1}{{f\left( x \right)}}\) đồng biến trên khoảng nào dưới đây?
\(\left( {3\,; + \infty } \right).\)
\[\left( { - 2\,;0} \right).\]
\(\left( {1\,;2} \right).\)
\(\left( { - \infty \,; - 1} \right).\)
Cho hàm số \(y = f(x)\) có bảng biến thiên như hình dưới:
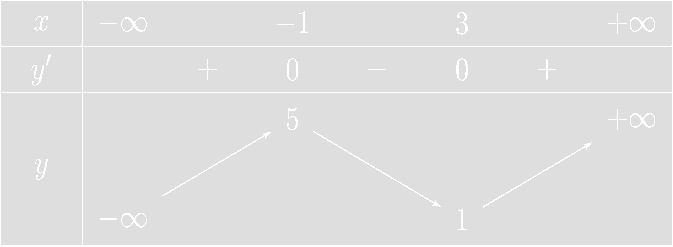
Số điểm cực trị của hàm số \(y = f\left( {{x^2} - 4x + 1} \right)\) là:
\(3\).
\(2\).
\(1\).
\(5\).
Cho hàm số \[y = f(x)\] liên tục trên \(\mathbb{R}\)và có đồ thị như hình vẽ bên. Hàm số có bao nhiêu điểm cực trị?
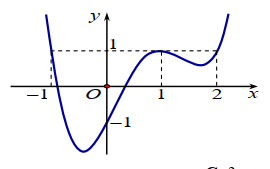
\[1\].
\[2\].
\[3\].
\[4\].
Cho hàm số \(y = f\left( x \right)\) có đồ thị \(y = f'\left( x \right)\) như hình sau. Hàm số \(g\left( x \right) = f\left( {3 - 2x} \right) + 2024\) đồng biến trên khoảng nào dưới đây?
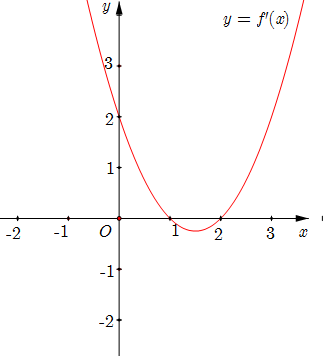
\(\left( {1; + \infty } \right)\).
\(\left( {\frac{1}{2};1} \right)\).
\(\left( {0;\frac{1}{2}} \right)\).
\(\left( { - \infty ;\frac{1}{2}} \right)\).
Cho hàm số \(y = f'\left( x \right)\) có đồ thị như hình bên. Tìm số điểm cực trị của hàm số \(g\left( x \right) = f\left( {{x^2} - 2x} \right)\) trên khoảng \(\left( {0; + \infty } \right)\).
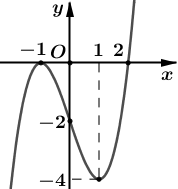
\(3\).
\(2\).
\(4\).
\(1\).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) thỏa mãn \(f\left( 2 \right) = f\left( { - 2} \right) = 0\) và đồ thị hàm số \(y = f'\left( x \right)\) có dạng như hình vẽ bên dưới.
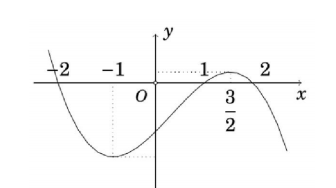
Hàm số \(g\left( x \right) = {\left( {f\left( x \right)} \right)^2}\) nghịch biến trên khoảng nào dưới đây?
\(\left( { - 2; - 1} \right)\).
\(\left( { - 1;\frac{3}{2}} \right)\).
\(\left( { - 1;1} \right)\).
\(\left( {1;2} \right)\).
Phần 2. Câu hỏi trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu hỏi, thí sinh chọn đúng hoặc chọn sai.
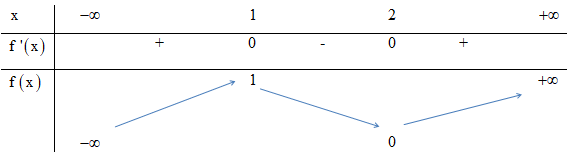
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
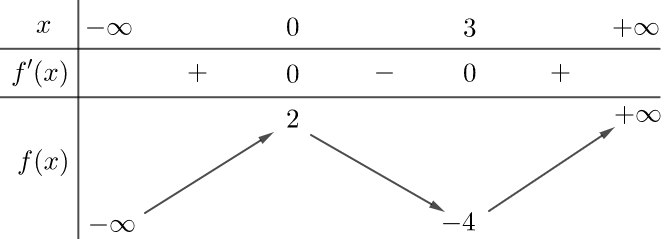
Mỗi khẳng định sau đây đúng hay sai?
a) Hàm số \(y = f\left( x \right)\)đồng biến trên khoảng \(( - \infty ;2).\)
b) Hàm số \(y = f\left( x \right)\)nghịch biến trên khoảng \((0;3).\)
c) Hàm số \(y = f\left( x \right)\)đạt cực đại tại \[x = 2.\]
d) Giá trị cực tiểu của hàm số \(y = f\left( x \right)\)là \[y = - 4.\]
Cho hàm số bậc ba \(y = f(x)\) có đồ thị là đường cong như hình vẽ sau
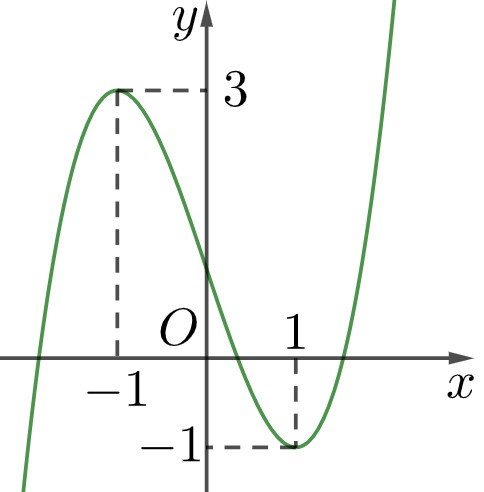
Mỗi khẳng định sau đây đúng hay sai?
a) Hàm số \(y = f(x)\)đồng biến trên khoảng \(( - \infty ;3).\)
b) Tổng giá trị cực đại và giá trị cực tiểu của hàm số \(y = f(x)\) là 2.
c) Hàm số \(y = f(x)\)có hai cực trị trái dấu.
d) Phương trình đường thẳng qua 2 điểm cực trị của đồ thị hàm số \(y = f(x)\)là \[d:y = - 3x\]
Cho hàm số \(y = \frac{1}{3}{x^3} + \left( {m + 1} \right){x^2} + \left( {{m^2} + 2m} \right)x - 3\), với \(m\) là tham số
a) Với mọi m hàm số luôn có hai điểm cực trị.
b) Hàm số luôn nghịch biến trên khoảng có độ dài bằng \(2\).
c) Không tồn tại giá trị của tham số \(m\) để hàm số đồng biến trên \(\mathbb{R}\).
d) Hàm số nghịch biến trên \(\left( { - 1;\,1} \right)\) khi và chỉ khi \(m \ge - 1\).
Cho hàm số \(y = \frac{{2{x^2} + 2x - 1 - 5m}}{{x - m}}\)
a) Hàm số xác định với mọi \(x\).
b) Có 2019 giá trị nguyên dương bé hơn 2024 của tham số \(m\)để hàm số \(y = \frac{{2{x^2} + 2x - 1 - 5m}}{{x - m}}\) nghịch biến trên khoảng \(\left( {1;5} \right)\).
c) \(m = 0\) thì hàm số có hai cực trị.
d) Nếu đồ thị hàm số có hai điểm cực trị thì hai điểm cực trị đó luôn nằm trên đường thẳng cố định.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Tìm khoảng đồng biến của hàm số \(y = \sqrt {1 - {x^2}} \)?
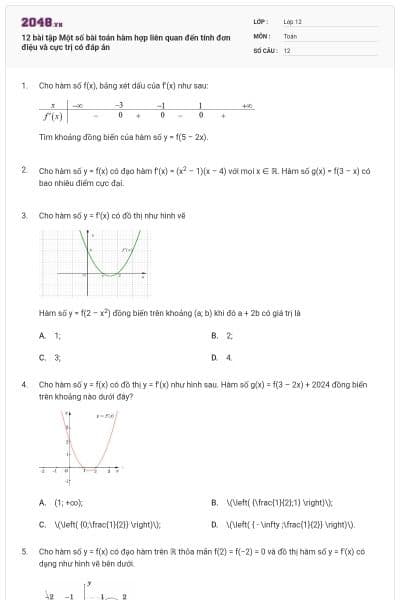
Cho hàm số \(f(x),\) xác định trên \(\mathbb{R},\) có bảng xét dấu hàm số \(f'(x)\) như sau
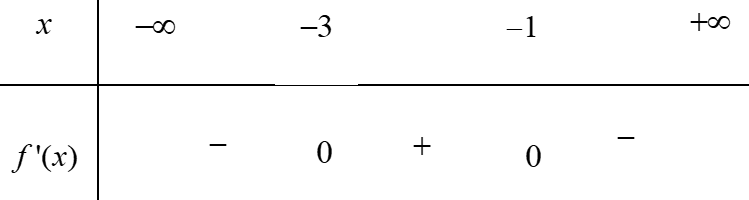
Tìm khoảng đồng biến của hàm số \(y = f(\sqrt {{x^2} - 4x} )\)?
Cho hàm số \[y = f\left( x \right)\] có đạo hàm \[f'\left( x \right) = \left( {x - 6} \right)\left( {{x^2} + 2x - 8} \right),\forall x \in \mathbb{R}.\]Có bao nhiêu giá trị nguyên dương của tham số \[m\]để hàm số \[g\left( x \right) = \left( {\left| {{x^3} + 3{x^2} + 8x + 6} \right| + m} \right)\]có ít nhất 3 điểm cực trị?
Có bao nhiêu giá trị nguyên của \(m\) thuộc đoạn \(\left[ { - 8;8} \right]\) để hàm số \(y = \left| {{x^3} - 3\left( {m + 2} \right){x^2} + 3m\left( {m + 4} \right)x + 5} \right|\) đồng biến trên khoảng \(\left( {1;3} \right)\)?
Độ giảm huyết áp của một bệnh nhân được đo bởi công thức \(G\left( x \right) = 0,25{x^2}\left( {30 - x} \right)\) trong đó \(x\left( {mg} \right)\) và x > 0 là lượng thuốc cần tiêm cho bệnh nhân. Để huyết áp giảm nhiều nhất thì cần tiêm cho bệnh nhân một liều lượng bằng bao nhiêu ?
Để thiết kế một chiếc bể cá hình chữ nhật có chiều cao là \(60cm,\) thể tích là \(96.000c{m^3}\), người thợ dùng loại kính để sử dụng làm mặt bên có giá thành 70.000 đồng/m2 và loại kính để làm mặt đáy có giá thành là 100.000 đồng/m2. Tính chi phí thấp nhất để hoàn thành bể cá.