Đề kiểm tra Tính đơn điệu và cực trị của hàm số (có lời giải) - Đề 3
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phướng án.
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ dưới
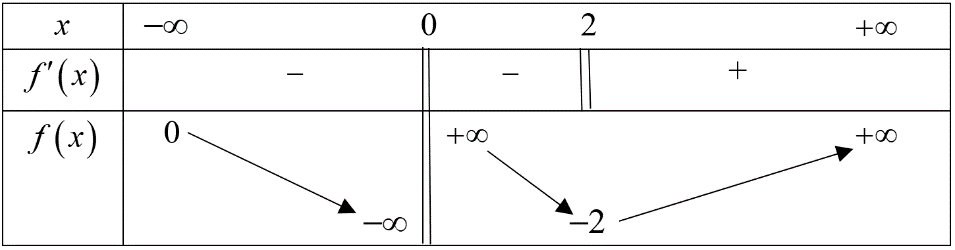
Mệnh đề nào sau đây sai?
Hàm số đồng biến trên khoảng \(\left( {2; + \infty } \right)\) .
Hàm số nghịch biến trên khoảng \(\left( { - \infty ;2} \right)\).
Hàm số đồng biến trên khoảng \(\left( {2\,;\,5\,} \right)\).
Hàm số nghịch biến trên khoảng \(\left( {0;\,2} \right)\).
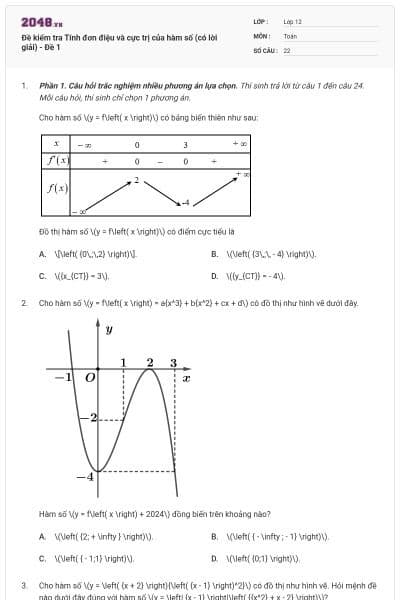
Cho hàm số \(y = f(x)\) có đồ thị là đường cong hình bên
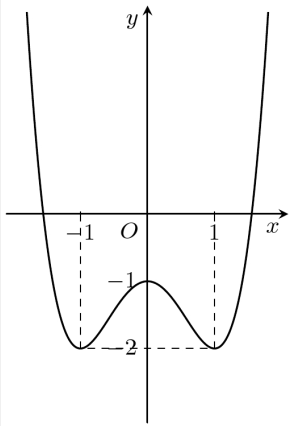
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
\((1; + \infty )\).
\((0;1)\).
\(( - 1;0)\).
\(( - \infty ;0)\).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {\left( {1 - x} \right)^2}{\left( {x + 1} \right)^3}\left( {3 - x} \right),\,\forall x \in \mathbb{R}\). Hàm số đã cho đồng biến trên khoảng nào dưới đây?
\(\left( { - \infty ;1} \right)\).
\(\left( { - \infty ; - 1} \right)\).
\(\left( { - 1;3} \right)\).
\(\left( {3; + \infty } \right)\).
Cho hàm số bậc bốn \(y = f\left( x \right)\). Hàm số \(y = f'\left( x \right)\)có đồ thị như hình vẽ
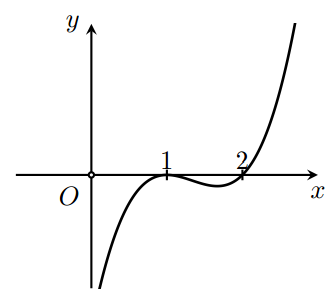
Hỏi hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?
\(\left( {0\,;1} \right)\).
\(\left( {0\,;\,2} \right)\).
\(\left( {2; + \infty } \right)\).
\(\left( {1\,;\,2} \right)\).
Cho hàm số \[y = \frac{{x + 1}}{{x - 1}}\]. Mệnh đề nào dưới đây đúng?
Hàm số đã cho nghịch biến trên \[\mathbb{R}\].
Hàm số đã cho đồng biến trên các khoảng \[\left( { - \infty ;\,1} \right)\] và \[\left( {1;\, + \infty } \right)\].
Hàm số đã cho nghịch biến trên khoảng \[\left( { - \infty ;\,1} \right)\] và đồng biến trên khoảng \[\left( {1;\, + \infty } \right)\].
Hàm số đã cho nghịch biến trên các khoảng \[\left( { - \infty ;1} \right)\] và \[\left( {1; + \infty } \right)\].
Cho hàm số \(y = \frac{x}{{{x^2} + 1}}\). Mệnh đề nào dưới đây đúng?
Hàm số đã cho nghịch biến trên \(\left( { - 1;\,1} \right)\).
Hàm số đã cho đồng biến trên \(\left( {1;\, + \infty } \right)\).
Hàm số đã cho nghịch biến trên \(\left( { - \infty ;\,1} \right)\).
Hàm số đã cho đồng biến trên \[\left( { - 1;\,1} \right)\].
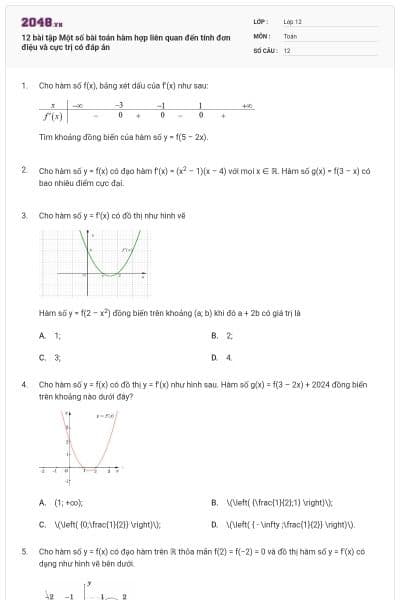
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
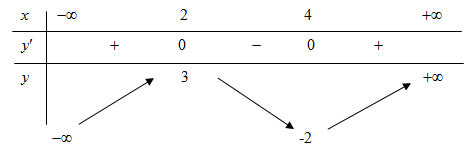
Hàm số đạt cực tiểu tại
\(x = 2\).
\(x = - 2\).
\(x = 4\).
\(x = 3\).
Cho hàm số bậc ba \[y = f\left( x \right)\] có đồ thị như hình bên dưới
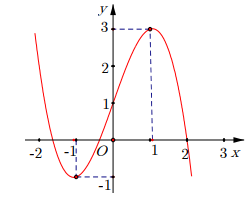
Hàm số có giá trị cực đại bằng
\(1\).
\(2\).
\( - 1\).
\(3\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \[\mathbb{R}\] và có bảng xét dấu của \(f'\left( x \right)\) như sau:
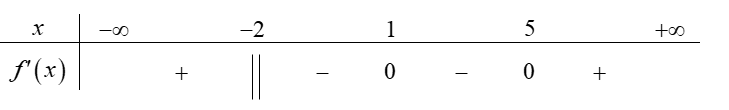
Tìm số điểm cực trị của hàm số đã cho.
\(1\).
\(2\).
\(3\).
\(0\).
Hàm số nào trong bốn hàm số được liệt kê dưới đây không có cực trị?
\(y = - {x^3} + x\).
\(y = {x^4}\).
\(y = \frac{{2x - 1}}{{x + 1}}\).
\(y = \left| x \right|\).
Cho hàm số \[y = f\left( x \right)\] có đạo hàm \(f'\left( x \right) = {x^2}\left( {x + 1} \right){\left( {x - 2} \right)^3}\), \(\forall x \in \mathbb{R}\). Hỏi hàm số đã cho có bao nhiêu điểm cực đại?
\(2\).
\(1\).
\(0\).
\(3\).
Cho hàm số \(y = {x^4} - 2{x^2} + 2\). Mệnh đề nào dưới đây đúng?
Hàm số đã cho đạt cực đại tại \(x = 2\).
Hàm số đã cho đạt cực đại tại \(x = 1\).
Hàm số đã cho đạt cực tiểu tại \(x = 0\).
Hàm số đã cho đạt cực tiểu tại \(x = - 1\).
PHẦN II. Câu trắc nghiệm đúng sai. Học sinh trả lời từ câu 1 đến câu 4. Mỗi ý a), b), c), d) ở mỗi câu, học sinh chọn đúng hoặc sai.
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình bên dưới
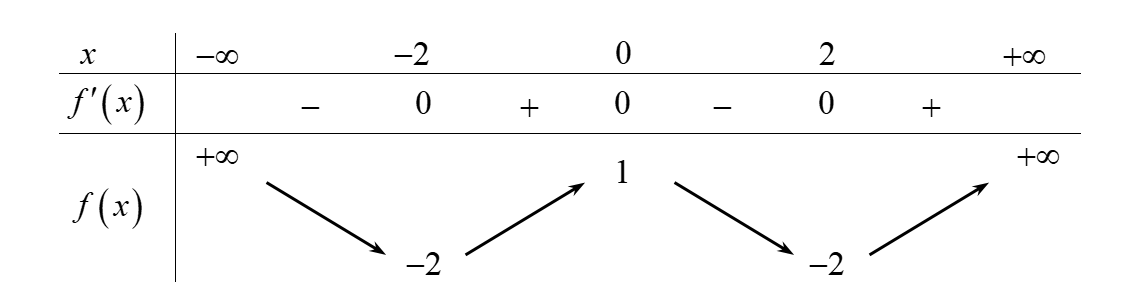
a)\(f\left( x \right)\) đồng biến trên khoảng \(\left( { - 2\,;\,0} \right)\).
b)\(f\left( x \right)\) nghịch biến trên khoảng \(\left( {0\,;\, + \infty } \right)\).
c)\(\forall {x_1},{x_2} \in \left( {2\,;\, + \infty } \right),{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
d)\[\forall {x_1},{x_2} \in \mathbb{R},\,f\left( {{x_1}} \right) = f\left( {{x_2}} \right) \Rightarrow {x_1} = {x_2}\].
Cho hàm số bậc bốn \[y = f\left( x \right)\]. Hàm số \(y = f'\left( x \right)\) có đồ thị như hình dưới đây
![Hàm số \[y = f\left( x \right)\] đồng biến trên khoảng \(\left( { - \infty \,;\,0} \right)\), (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/screenshot-3626-1759133053.png)
a)Hàm số\[y = f\left( x \right)\] đồng biến trên khoảng\(\left( { - \infty \,;\,0} \right)\),
b)Hàm số đồng biến trên khoảng\(\left( { - 1\,;\,1} \right)\).
c)Hàm số\[y = f\left( x \right)\] nghịch biến trên khoảng\(\left( { - \infty \,;\,0} \right)\).
d) Hàm số\[y = f\left( x \right)\] nghịch biến trên khoảng\(\left( {1\,;\,2} \right)\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng xét dấu \(f'\left( x \right)\) dưới đây
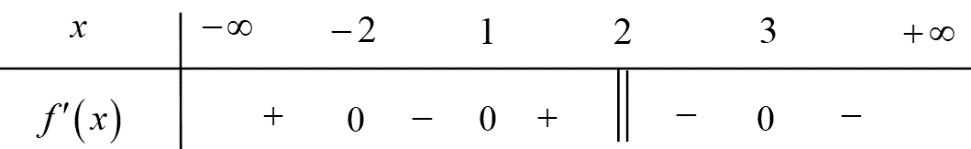
a) Hàm số đã cho đạt cực đại tại \(x = - 2\).
b) Giá trị cực tiểu của hàm số đã cho là \(f\left( 1 \right)\).
c) Điểm cực tiểu của đồ thị hàm số đã cho là \(x = 1\).
d) Hàm số đã cho đạt cực đại tại \(x = 2\).
Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị như hình vẽ bên
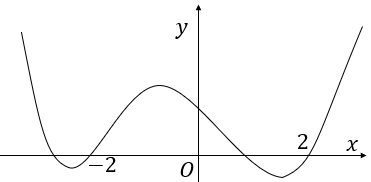
a) Hàm số đã cho có một điểm cực đại và hai điểm cực tiểu.
b) Hàm số đã cho có \(4\) điểm cực trị.
c) Số điểm cực trị của hàm số \(g\left( x \right) = f\left( {\left| x \right|} \right)\) là \(7\).
d) Số điểm cực trị của hàm số \(h\left( x \right) = \left| {f\left( x \right)} \right|\) là \(7\).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Học sinh trả lời từ câu 1 đến câu 6.Tìm tất cả các khoảng nghịch biến của hàm số \(y = \frac{{{x^2} + 2x + 2}}{{x + 1}}\).
Cho hàm số bậc ba \[y = f\left( x \right)\]. Hàm số \(y = f'\left( x \right)\) có đồ thị như hình dưới đây
![Tìm tất cả các khoảng đồng biến của hàm số \[y = f\left( {2 - {x^2}} \right)\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/13-1759133388.png)
Tìm tất cả các khoảng đồng biến của hàm số \[y = f\left( {2 - {x^2}} \right)\].
Hằng ngày mực nước của một con kênh lên xuống theo thủy triều. Độ sâu \(h\,\,\left( {\rm{m}} \right)\) của mực nước trong kênh tại thời điểm \(t\,\,\left( {\rm{h}} \right)\,\,\left( {0 \le t \le 24} \right)\) trong ngày được xác định bởi công thức \(h = 2\cos \left( {\frac{{\pi t}}{{12}} + \frac{\pi }{3}} \right) + 5\). Gọi \(\left( {a\,;\,b} \right)\) là khoảng thời gian trong ngày mà độ sâu của mực nước trong kênh tăng dần. Tính giá trị của \(a + b\).
Xí nghiệp \(A\) sản xuất độc quyền một loại sản phẩm. Biết rằng hàm tổng chi phí sản xuất là \(TC = {x^3} - 77{x^2} + 1000x + 40000\) và hàm doanh thu là \(TR = - 2{x^2} + 1312x\), với \(x\) là số sản phẩm. Lợi nhuận của xí nghiệp \(A\) được xác định bằng hàm số \(f\left( x \right) = TR - TC\), cực đại lợi nhuận của xí nghiệp \(A\) khi đó đạt bao nhiêu sản phẩm?
Khi loại thuốc A được tiêm vào bệnh nhân, nồng độ \[mg/l\]của thuốc trong máu sau \[x\]phút được xác định bởi công thức: \[C(x) = \frac{{30x}}{{{x^2} + 2}}\].
. Calculus. Cengage Learning)
Để đưa ra những lời khuyên và cách xử lí phù hợp cho bệnh nhân, ta cần tìm khoảng thời gian mà nồng độ của thuốc trong máu đang tăng. Em hãy cho biết hàm nồng độ thuốc trong máu \[C(x)\] đạt giá trị cực đại là bao nhiêu trong khoảng thời gian \[6\] phút sau khi tiêm ?
Một tấm bạt hình vuông cạnh \(20\,m\)như hình vẽ dưới đây. Người ta dự tính cắt phần tô đậm của tấm bạt rồi gập và may lại , nhằm mục đích phủ lên tháp đèn trang trí để tránh hư hại tháp khi trời mưa.
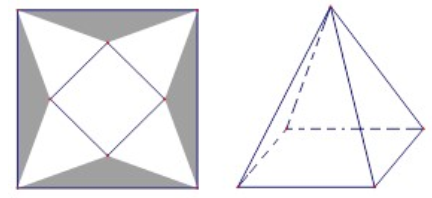
Biết khối chóp hình thành sau khi gập và may lại cần thể tích lớn nhất thì mới phủ kín tháp đèn. Hỏi phần diện tích tấm bạt bị cắt là bao nhiêu để đảm bảo yêu cầu trên.