Đề kiểm tra Tính đơn điệu và cực trị của hàm số (có lời giải) - Đề 2
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
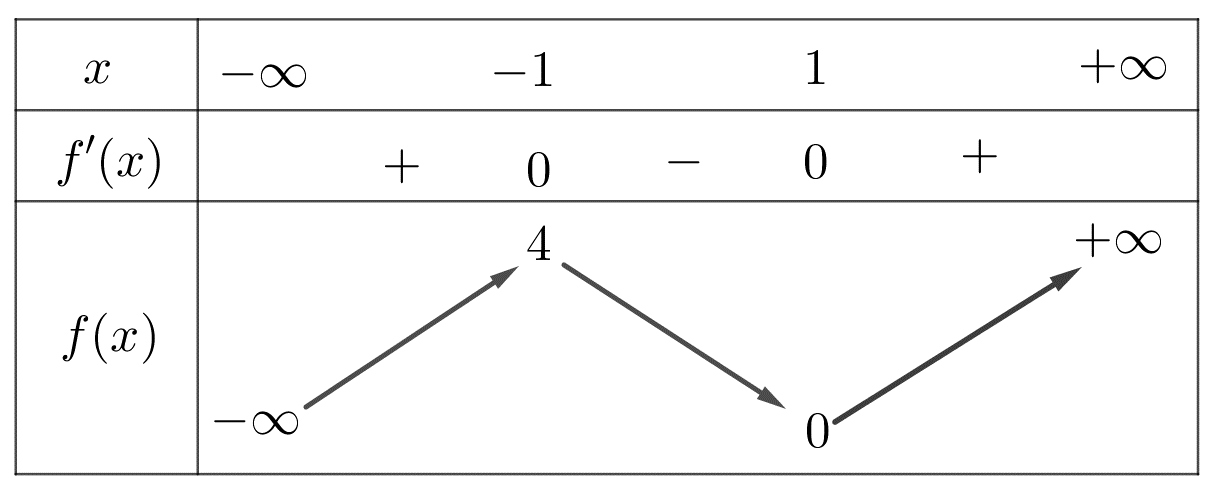
Hàm số đã cho đồng biến trên khoảng nào dưới đây
\(\left( { - \infty ;4} \right)\).
\(\left( {2; + \infty } \right)\).
\(\left( { - 1;1} \right)\).
\(\left( { - \infty ; - 1} \right) \cup \left( {1; + \infty } \right)\).
Cho hàm số \(y = a{x^4} + b{x^2} + c\) có đồ thị như hình vẽ
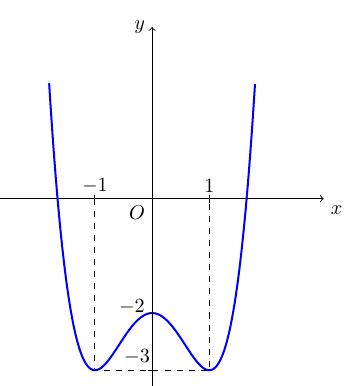
Điểm cực đại của hàm số đã cho là
\(x = 0\).
\(x = - 1\).
\(x = 1\).
\(x = - 2\).
Cho hàm số \[y = f\left( x \right)\] có đạo hàm trên \[\mathbb{R}.\] Đồ thị hàm số \[y = f'\left( x \right)\] như hình vẽ
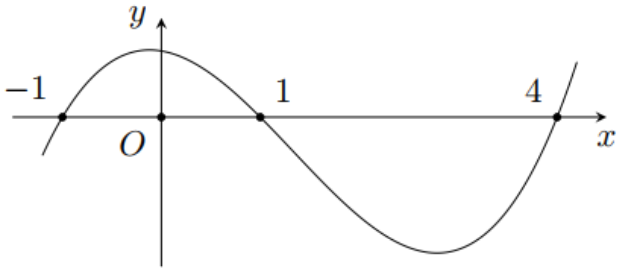
Khẳng định nào sau đây đúng?
Hàm số \[y = f\left( x \right)\] đồng biến trên khoảng \[\left( {1;4} \right)\].
Hàm số \[y = f\left( x \right)\] nghịch biến trên khoảng \[\left( { - 1;4} \right)\].
Hàm số \[y = f\left( x \right)\] đồng biến trên khoảng \[\left( { - 1;1} \right)\].
Hàm số \[y = f\left( x \right)\] nghịch biến trên khoảng \[\left( { - 1;1} \right)\].
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng xét dấu của đạo hàm như hình vẽ.
![Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng xét dấu của đạo hàm như hình vẽ. Hàm số \(y = f\left( x \right)\) có bao nhiêu điểm cực trị? A. \[1\]. B. \[2\]. C. \[3\]. D. \[4\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/4-1759131516.png)
Hàm số \(y = f\left( x \right)\) có bao nhiêu điểm cực trị?
\[1\].
\[2\].
\[3\].
\[4\].
Cho hàm số \(y = - {x^3} - 3{x^2} + 4\). Mệnh đề nào dưới đây đúng?
Hàm số nghịch biến trên khoảng \(\left( { - 2;0} \right)\).
Hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\).
Hàm số đồng biến trên khoảng \(\left( { - \infty ; - 2} \right)\).
Hàm số đồngbiến trên khoảng \(\left( { - 2;0} \right)\).
Cho hàm số \(y = \frac{{{x^2} - 2x + 5}}{{x - 1}}\). Mệnh đề nào dưới đây đúng?
Hàm số nghịch biến trên khoảng \(\left( { - 1;\,1} \right) \cup \left( {1\,;\,3} \right)\).
Hàm số nghịch biến trên khoảng \(\left( { - 1;\,3} \right){\rm{\backslash }}\left\{ 1 \right\}\).
Hàm số nghịch biến trên mỗi khoảng \(\left( { - 1;\,1} \right)\)và \(\left( {1\,;\,3} \right)\).
Hàm số nghịch biến trên khoảng \(\left( { - \infty ; - 1} \right)\).
Hàm số \(y = \sqrt { - {x^2} + 2x} \) đồng biến trên khoảng nào?
\(\left( {0\,;\,1} \right)\).
\(\left( {1\,;\,2} \right)\).
\(\left( { - \infty ;0} \right)\).
\(\left( {2\,;\, + \infty } \right)\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\), có đạo hàm \(f'\left( x \right) = 2x{\left( {x - 1} \right)^2}{\left( {2 - x} \right)^3}\). Tìm điểm cực tiểu của hàm số.
\(x = 1\).
\(x = 0\).
\(y = 0\).
\(x = 2\).
Cho hàm số nào \(y = f\left( x \right)\) có đạo hàm \[f'\left( x \right) = x\left( {{x^2} - 1} \right){\left( {x - 2} \right)^2}.\] Số điểm cực tiểu của đồ thị hàm số là
\(4.\)
\(1.\)
\(2.\)
\(3.\)
Hàm số \[y = \left( {{x^2} - 3} \right){{\rm{e}}^x}\] nghịch biến trên khoảng nào trong các khoảng dưới đây?
\(\left( { - \infty ; - 3} \right)\).
\(\left( { - 1;3} \right)\).
\(\left( { - 3;1} \right)\).
\(\left( {1;\, + \infty } \right)\).
Hàm số \[y = {\log _5}\left( {10x - {x^2}} \right)\] đồng biến trên khoảng nào trong các khoảng dưới đây?
\(\left( {5;10} \right)\).
\(\left( {0;10} \right)\).
\(\left( {0;5} \right)\).
\(\left( {10;\, + \infty } \right)\).
Có bao nhiêu giá trị nguyên của tham số \[m\] để hàm số \[y = {x^3} - 3m{x^2} + 3\left( {2m + 3} \right)x + 1\] đồng biến trên \[\mathbb{R}\].
\[5\].
\[3\].
\[4\].
\[6\].
PHẦN II. Câu trắc nghiệm đúng sai.
Cho hàm số \(y = {x^3} + 3{x^2} - mx + 1\).
a) \(y' = 3{x^2} + 6x - m\).
b) Với \(m = 9\), hàm số đồng biến trên khoảng \(\left( { - 3\,;\,1} \right)\).
c) Với \(m = - 3\), hàm số nghịch biến trên khoảng \(\left( { - \infty \,;\, - 1} \right)\).
d) Hàm số đồng biến trên khoảng \(\left( { - \infty \,;\,0} \right)\) khi \(m \le - 3\).
Cho hàm số \(y = \frac{{{x^2} + 3x + 3}}{{x + 2}}\) có đồ thị \(\left( C \right)\) và \(A\), \(B\) là hai điểm cực trị của \(\left( C \right)\).
a) \(y' = \frac{{{x^2} + 4x + 3}}{{{{\left( {x + 2} \right)}^2}}}\).
b) \(A\) và \(B\) nằm ở hai phía của trục tung.
c) Đường thẳng \(AB\)có phương trình là \(y = 2x + 1\).
d) \(A\) và \(B\) đối xứng nhau qua đường thẳng \(\Delta \) có phương trình là \(x + 2y + 4 = 0\).
Cho hàm số \(y = {\log _2}\left( {m{x^2} + x + m} \right)\)
a) \(m = 0\) hàm số đồng biến trên khoảng \(\left( {0;\, + \infty } \right)\).
b) \(m = 1\) hàm số nghịch biến trên khoảng \(\left( { - \infty ;\,0} \right)\) và đồng biến trên khoảng \(\left( {0;\, + \infty } \right)\).
c) \(y' = \frac{{2mx + 1}}{{m{x^2} + x + m}}\).
d) \(m \in \left[ { - \frac{1}{4};\,\frac{1}{2}} \right)\) thì hàm số có tập xác định \(D = \mathbb{R}\) và đồng biến trên khoảng \(\left( {2;\, + \infty } \right)\).
Cho hàm số \(y = \sqrt {{x^2} - 2mx + 9} \)
a)\(m = 0\) hàm số không có cực trị.
b) \(m = 1\) hàm số đạt cực tiểu tại \(x = 1\).
c) \(y' = \frac{{x - m}}{{\sqrt {{x^2} - 2mx + 9} }}\).
d) Có 7 giá trị \(m\) nguyên để hàm số có cực trị.
PHẦN III. Câu trắc nghiệm trả lời ngắn.
Cho hàm số \[y = f\left( x \right)\] liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ.
![PHẦN III. Câu trắc nghiệm trả lời ngắn. Câu 17. Cho hàm số \[y = f\left( x \right)\] liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/12-1759132112.png)
Gọi \(A\left( {a;b} \right)\) là điểm cực tiểu của đồ thị hàm số đã cho. Tính giá trị biểu thức \(P = 2a - b\).
Biết hàm số \[f\left( x \right) = \frac{1}{5}{x^5} - {x^4} + {x^3}\] nghịch biến trên khoảng \(\left( {a;b} \right)\) có độ dài bằng \(2\). Tính giá trị biểu thức \(P = a.b\).
Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = \frac{{x + {m^2}}}{{x + 4}}\)đồng biến trên từng khoảng xác định của nó
Thể tích của nước tại nhiệt độ được tính bởi công thức .Thể tích nước giảm trong khoảng nhiệt độ làm tròn đến hàng đơn vị. Tổng bằng bao nhiêu?
Hàm số \[y = - \frac{x}{4} + {\cos ^2}\frac{x}{2}\] có bao nhiêu điểm cực đại trên đoạn \(\left[ { - \pi ;\pi } \right]\)?
Một chất điểm chuyển động theo phương trình \(s\left( t \right) = - \frac{{{t^3}}}{3} + 18{t^2} - 35t + 10\), trong đó \(t\) tính bằng giây và \(s\)tính bằng mét. Trong 40 giây đầu tiên, chất điểm có vận tốc tức thời giảm trong khoảng thời gian \(\left( {a;b} \right)\). Tính giá trị của biểu thức \(P = 2b - 3a\).