22 câu trắc nghiệm Toán 12 Kết nối tri thức Bài 1. Tính đơn điệu và cực trị hàm số (Đúng sai - Trả lời ngắn) có đáp án
37 câu hỏi
Cho hàm số 
. Mệnh đề nào dưới đây đúng?
Hàm số luôn luôn đồng biến trên ℝ\{1}.
Hàm số nghịch biến trên các khoảng (−∞; 1) và (1; +∞).
Hàm số đồng biến trên các khoảng (−∞; 1) và (1; +∞).
Hàm số luôn luôn nghịch biến trên (−∞; 1) È (1; +∞).
Hàm số f(x) = x3 + 3x2 + 3x + 2.
Đồng biến trên khoảng (−∞; −1).
Đồng biến trên khoảng (−1; +∞).
Đồng biến trên khoảng (−∞; −1) È (−1; +∞).
Đồng biến trên ℝ.
Cho hàm số y = f(x) có bảng biến thiên sau:
Hàm số y = f(x) đồng biến trên khoảng nào sau đây?
(−∞; 5).
(0; 2).
(2; +∞).
(0; +∞).
Cho hàm số y = f(x) có bảng biến thiên như hình dưới đây
Tìm mệnh đề đúng trong các mệnh đề sau
Hàm số đồng biến trên khoảng (−∞; 3).
Hàm số nghịch biến trên khoảng (−2; +∞).
Hàm số nghịch biến trên khoảng (−∞; −2).
Hàm số đồng biến trên khoảng (−4; −1).
Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Hàm số đồng biến trên khoảng nào dưới đây?
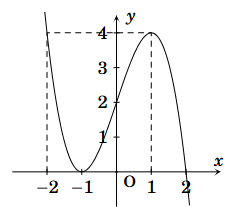
(−1; 1).
(−2; 0).
(1; 2).
(−1; 2).
Cho hàm số y = f(x) xác định, liên tục trên ℝ và có đạo hàm f'(x). Biết rằng f'(x) có đồ thị như hình vẽ.
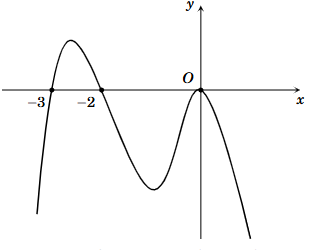
Mệnh đề nào sau đây đúng.
Hàm số y = f(x) đồng biến trên khoảng (−2; 0).
Hàm số y = f(x) nghịch biến trên khoảng (0; +∞).
Hàm số y = f(x) đồng biến trên khoảng (−∞; 3).
Hàm số y = f(x) nghịch biến trên khoảng (−3; −2).
Cho hàm số y = f(x) có bảng biến thiên như sau
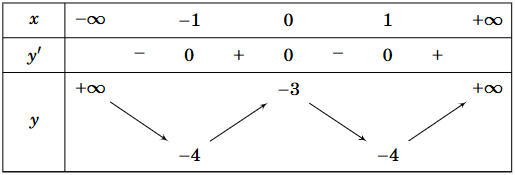
Hàm số đạt cực đại tại điểm
x = −1.
x = 1.
x = 0.
x = −3.
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ. Khẳng định nào sau đây sai?
Hàm số đạt cực đại tại x = 0 và x = 1.
Giá trị cực tiểu của hàm số bằng −1.
Giá trị cực đại của hàm số bằng 2.
Hàm số đạt cực tiểu tại x = −2.
Tìm số điểm cực tiểu trên đoạn [−2; 4] của hàm số y = f(x) biết hàm số y = f'(x) có đồ thị như hình vẽ
1.
0.
2.
3.
Cho hàm số y = x3 – 3x2 – 9x + 1. Tổng các giá trị cực đại và cực tiểu của đồ thị hàm số bằng
−6.
−26.
−20.
20.
Cho hàm số 
. Mệnh đề nào dưới đây đúng?
Hàm số đạt cực đại tại x = 4.
Hàm số không có cực trị.
Hàm số đạt cực tiểu tại x = 0.
Hàm số có 2 điểm cực trị.
Cho hàm số 
. Mệnh đề nào dưới đây đúng?
Điểm cực tiểu của hàm số bằng −3.
Điểm cực tiểu của hàm số bằng 1.
Điểm cực tiểu của hàm số bằng −6.
Điểm cực tiểu của hàm số bằng 2.
a) Tập xác định của hàm số là (1; +∞).
b) Hàm số có đạo hàm là y' = 3x2 + 6x + 9
c) Hàm số đồng biến trên khoảng (−3; 1).
d) Đồ thị hàm số đạt cực trị tại 2 điểm A, B. Chu vi của tam giác OAB bằng 
(với O là gốc tọa độ).
Hàm số đồng biến trên khoảng (7; +∞)
b) f(1) < f(3)
c) Hàm số nghịch biến trên khoảng (1; 7)
d) Phương trình f'(3x – 1) = 0 nhận 
làm nghiệm
a) Hàm số đã cho có một điểm cực trị
b) Giá trị cực đại của hàm số bằng 3
c) Điểm cực đại của đồ thị hàm số nằm dưới đường thẳng y = 5.
d) Hàm số 
có đúng một điểm cực trị.
a) Điểm cực tiểu của hàm số đã cho là x = 7
b) f(7) là giá trị cực đại của hàm số đã cho
c) Hàm số đồng biến trên khoảng (7; +∞)
d) f(11) > f(7)
a) Tốc độ truyền bệnh đến ngày thứ t là f'(t) = −3t2 + 90t.
b) Khoảng thời gian mà tốc độ truyền bệnh giảm là (0; 15)
c) Trong 25 ngày đầu thì tốc độ truyền bệnh lớn nhất là ở ngày thứ 25.
d) Trong 25 ngày đầu thì ngày có số người nhiễm bệnh nhiều nhất đạt tới 675 người.
PHẦN III. TRẢ LỜI NGẮN
Cho hàm số 
có điểm cực tiểu x = x1 và điểm cực đại bằng x = x2. Tính P = −2x1 + x2.
Cho hàm số y = f(x) có đạo hàm là hàm số y = f'(x) liên tục trên ℝ và y = f'(x) có đồ thị như hình vẽ dưới đây. Tìm số khoảng đồng biến của hàm số.
Cho hàm số y = f(x) có bảng biến thiên như sau:
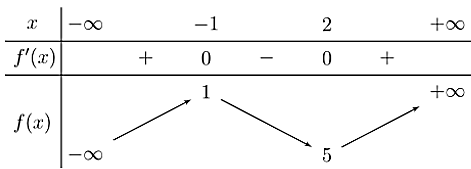
Phương trình f'(f(x)) = 0 có bao nhiêu nghiệm thực phân biệt.
Cho hàm số y = f(x) có đạo hàm f'(x) = (x2 – 4)(x2 – 2x), ∀x Î ℝ. Biết hàm số y = f(x) nghịch biến trên khoảng (a; b). Tính b – a.
Biết đồ thị hàm số y = x3 – 3x2 + 2ax + b (a; b Î ℝ) có điểm cực tiểu A(2; −2). Tính a + b.
