Đề kiểm tra Tính đơn điệu và cực trị của hàm số (có lời giải) - Đề 1
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 24. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
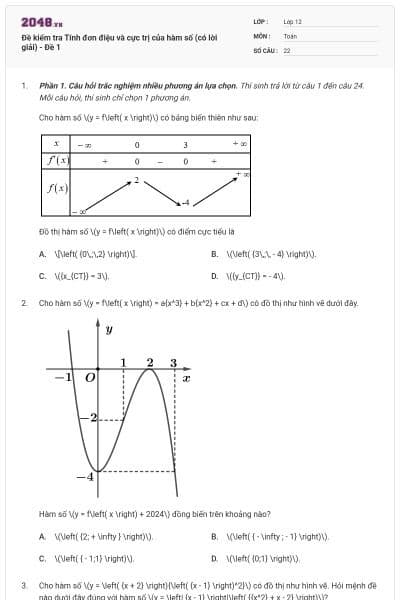
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
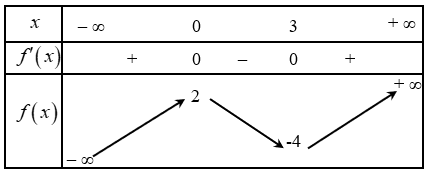
Đồ thị hàm số \(y = f\left( x \right)\) có điểm cực tiểu là
\[\left( {0\,;\,2} \right)\].
\(\left( {3\,;\, - 4} \right)\).
\({x_{CT}} = 3\).
\({y_{CT}} = - 4\).
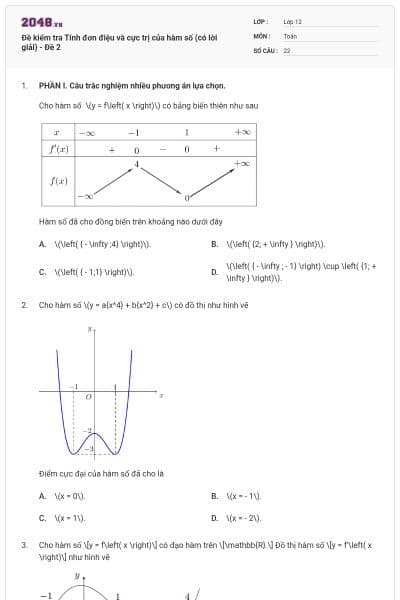
Cho hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ dưới đây.
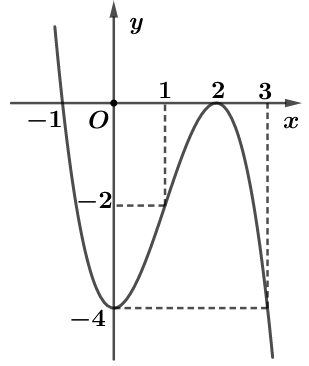
Hàm số \(y = f\left( x \right) + 2024\) đồng biến trên khoảng nào?
\(\left( {2; + \infty } \right)\).
\(\left( { - \infty ; - 1} \right)\).
\(\left( { - 1;1} \right)\).
\(\left( {0;1} \right)\).
Cho hàm số \(y = \left( {x + 2} \right){\left( {x - 1} \right)^2}\) có đồ thị như hình vẽ. Hỏi mệnh đề nào dưới đây đúng với hàm số \(y = \left| {x - 1} \right|\left( {{x^2} + x - 2} \right)\)?
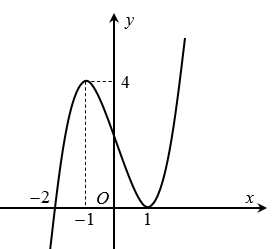
Hàm số đồng biến trên khoảng \(\left( { - \infty ; - 2} \right)\).
Hàm số nghịch biến trên khoảng \(\left( { - \infty ; - 1} \right)\).
Hàm số đồng biến trên khoảng \(\left( { - 2;1} \right)\).
Hàm số nghịch biến trên khoảng \(\left( { - 1;1} \right)\).
Cho hàm số \[y = \frac{1}{3}{x^3} - \frac{{{m^2} + 3}}{2}{x^2} - \left( {{m^3} + m - 2} \right)x + {m^2}\] có điểm cực tiểu, điểm cực đại lần lượt là \[{x_{{\rm{CT}}}}\], . Số giá trị nguyên trong đoạn \[\left[ { - 9;9} \right]\] của \(m\) thỏa mãn là
\[8\].
\[9\].
\[6\].
\[11\].
Cho hàm số \(f\left( x \right)\) có bảng xét dấu của đạo hàm như sau
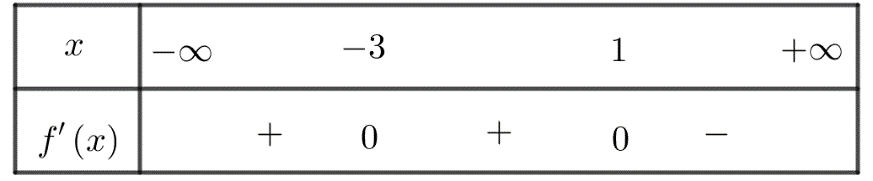
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
\(\left( {2; + \infty } \right)\).
\(\left( { - \infty ; - 2} \right)\).
\(\left( { - 2; + \infty } \right)\).
\(\left( { - 2;1} \right)\).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \left( {x + 1} \right)\left( {x - 4} \right),\,\forall x \in \mathbb{R}\). Điểm cực tiểu hàm số đã cho là
\[x = 1\].
\[x = 4\].
\[x = - 1\].
\[x = - 4\].
Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = {x^4} - 12{x^2} + \left( {m - 2} \right)x\) có ba điểm cực trị?
\(47.\)
\(44.\)
\(46.\)
\(45.\)
Cho hàm số bậc năm \(y = f\left( x \right)\) và đồ thị hàm số \(y = f'\left( x \right)\) là đường cong trong hình vẽ dưới đây
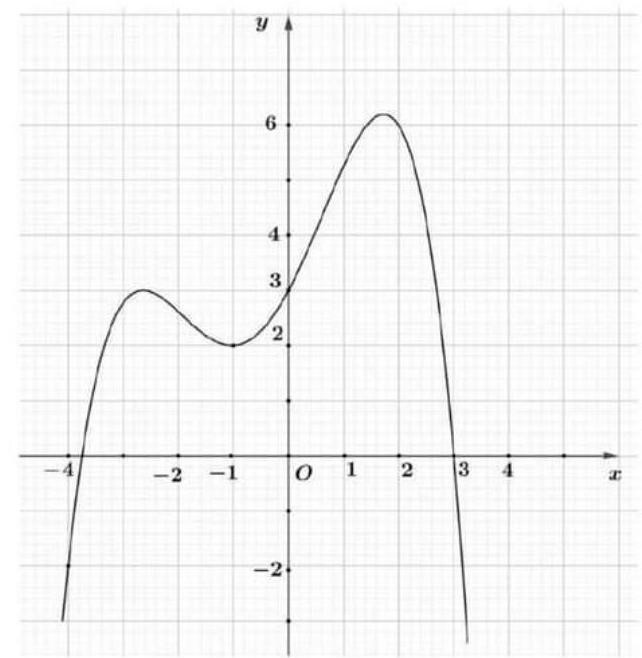
Xét hàm số \(g\left( x \right) = 3f\left( { - {x^3} - x + m + 3} \right) + \left( {{x^3} + x - m - 3} \right){\left( {{x^3} + x - m} \right)^2},m\) là tham số. Số giá trị nguyên của \(m\) thuộc nửa khoảng \(\left( { - 100;100} \right]\) để hàm số \(g\left( x \right)\) đồng biến trên khoảng \(\left( {0;3} \right)\) là
\(167\).
\(168\).
\(169\).
\(166\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau :
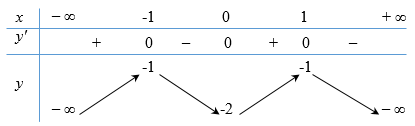
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
\(\left( {0;1} \right)\)
\(\left( {1; + \infty } \right)\)
\(\left( { - \infty ;1} \right)\)
\(\left( { - 1;0} \right)\)
Cho hàm số \[y = \frac{{x - 2}}{{x + 1}}\]. Mệnh đề nào dưới đây đúng?
Hàm số nghịch biến trên khoảng \[\left( { - \infty ; + \infty } \right)\]
Hàm số nghịch biến trên khoảng \[\left( { - 1; + \infty } \right)\]
Hàm số nghịch biến trên khoảng \[\left( { - \infty ; - 1} \right)\]
Hàm số đồng biến trên khoảng \[\left( { - \infty ; - 1} \right)\]
Hàm số nào dưới đây đồng biến trên khoảng \(\left( { - \infty ; + \infty } \right)\)?
\(y = \frac{{x - 1}}{{x - 2}}\)
\(y = {x^3} + 2x\)
\(y = - {x^3} - 3x\)
\(y = \frac{{x + 1}}{{x + 3}}\)
Cho hàm số \(f\left( x \right)\), bảng xét dấu của \(f'\left( x \right)\) như sau:
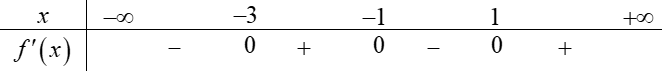
Hàm số \(y = f\left( {5 - 2x} \right)\) đồng biến trên khoảng nào dưới đây?
\(\left( {3\,;\,4} \right)\).
\(\left( {1\,;\,3} \right)\).
\(\left( { - \infty \,;\, - 3} \right)\).
\(\left( {4\,;\,5} \right)\).
PHẦN 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \[y = 2{x^3} + 2\left( {m + 1} \right){x^2} + 6x + 4 + 2m\] . Khi đó:
a) Khi \(m = - 1\) thì hàm số đồng biến trên \(\left( { - \infty ; + \infty } \right)\)
b) Hàm số \[y = 2{x^3} + 2\left( {m + 1} \right){x^2} + 6x + 4 + 2m\] không có cực trị khi \(m = 1\)
c) Có 3 giá trị nguyên dương của tham số \[m\] để hàm số \[y = 2{x^3} + 2\left( {m + 1} \right){x^2} + 6x + 4 + 2m\] đồng biến trên \[\mathbb{R}\]
d) Hàm số \[y = 2{x^3} + 2\left( {m + 1} \right){x^2} + 6x + 4 + 2m\] đạt cực tiểu tại \(x = 2\) khi đó \(m \in \left( {2;5} \right)\)
Cho hàm số\(y = 2{x^3} - 6{x^2} + 2\left( {2 - m} \right)x + m\). Khi đó:
a) Có 5 giá trị nguyên dương để hàm số đồng biến trên khoảng \(\left( { - \infty ; + \infty } \right)\)
b) Có \(2025\)giá trị nguyên của \(m \in \left[ { - 2024;2024} \right]\) để hàm số có hai điểm cực trị.
c) Biết tập hợp tất cả các giá trị thực của tham số \(m\) để hàm số đồng biến trên khoảng \(\left( {2; + \infty } \right)\)là \(\left( { - \infty ;a} \right]\) lúc đó: \(\left( { - \infty ;a} \right] \cap \left( {3;2025} \right) = \left( { - \infty ;2025} \right)\)
d) Biết tập hợp tất cả các giá trị thực của tham số \(m\) để hàm số đồng biến trên khoảng \(\left( {2; + \infty } \right)\)là \(\left( { - \infty ;a} \right]\)lúc đó, phương trình \({8^x} = a\) có nghiệm \(x > 2\)
Cho hàm số \(y = \frac{{(m + 1){x^2} - 2mx + 6m}}{{x - 1}}\). Các mệnh đề sau đúng hay sai?
a)Với \(m = - 1\) thì hàm số đồng biến trên \(\left( {2; + \infty } \right)\)
b) Với \(m = 0\) thì hàm số nghịch biến trên \(\left( {1; + \infty } \right)\)
c) Hàm số đồng biến trên mỗi khoảng xác định khi và chỉ khi \(m\) thuộc \(\left[ {a;b} \right]\). Khi đó \(a + 5b = 0\)
d) Điều kiện cần và đủ để hàm số đồng biến trên \(\left( {4; + \infty } \right)\) là \(m \in \left[ { - 1; + \infty } \right)\).
Cho hàm số \(y = {x^4} - 2m{x^2} + 2{m^4} - m\), trong đó \(m\)là tham số. Các mệnh đề sau đúng hay sai?
a) Với mọi \(m\)dương hàm số luôn có 3 điểm cực trị.
b) Với \(m < 0\)hàm số đạt cực đại tại \(x = 0\).
c) Hàm số luôn luôn có một điểm cực tiểu với mọi giá trị của tham số \(m\).
d) Không tồn tại giá trị thực của tham số \(m\) sao cho đồ thị hàm số có ba điểm cực trị đều thuộc các trục toạ độ.
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Cho hàm số \[y = f\left( x \right)\] có đạo hàm \[f'\left( x \right) = \,\left( {{x^2} - 1} \right)\left( {x - 4} \right)\] với mọi \[x \in \mathbb{R}\]. Hàm số \[g\left( x \right)\, = \,f\left( {3 - x} \right)\] có số điểm cực đại là?
Cho hàm số \[y = f'\left( x \right)\]có đồ thị như hình vẽ
![Cho hàm số \[y = f'\left( x \right)\]có đồ thị như hình vẽ Hàm số \[y = f\left( {2 - {x^2}} \right)\] đồng biến trên khoảng khi đó \[a + 2b\]có giá trị là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/14-1759131083.png)
Hàm số \[y = f\left( {2 - {x^2}} \right)\] đồng biến trên khoảng khi đó \[a + 2b\]có giá trị là
Gọi \(S\) là tập hợp tất cả các giá trị nguyên của \(m\) sao cho hàm số
\(y = \left| { - {x^4} + m{x^3} + 2{m^2}{x^2} + m - 1} \right|\) đồng biến trên \(\left( {1;\, + \infty } \right)\) Tổng tất cả các phần tử của \(S\) là
Cho hàm số \[y = f\left( x \right)\] có đạo hàm là \[f'\left( x \right) = \left( {{x^2} + 9x} \right)\left( {{x^2} - 9} \right),\]với mọi \[x \in \mathbb{R}\]. Có bao nhiêu giá trị nguyên của tham số \[m\] để hàm số \[g\left( x \right) = f\left( {\left| {{x^3} + 3x} \right| + 2m - {m^2}} \right)\] có không quá \[6\] điểm cực trị?
Một chuyển động thẳng được xác định bởi phường trình \(S\left( t \right) = \frac{1}{3}{t^3} - 3{t^2} + 5t + 2\) với \(t > 0\), \(t\) tính bằng giây và \(S\) tính bằng mét. Trong khoảng thời gian nào vận tốc của vật tăng?
Một con cá hồi bơi ngược dòng để vượt khoảng cách là\(300\,km\) . Vận tốc dòng nước là \(6\,km{\rm{/}}h\). Nếu vận tốc bơi của cá khi nước đứng yên là \(v\,\left( {km{\rm{/}}h} \right)\)thì năng lượng tiêu hao của cá trong \(t\)giờ được cho bởi công thức \(E\left( v \right) = c{v^3}t\), trong đó \(c\)là hằng số và \(E\) tính bằng Jun. Vận tốc bơi của cá khi nước đứng yên nằm ở khoảng nào thì năng lượng tiêu hao của cá giảm?