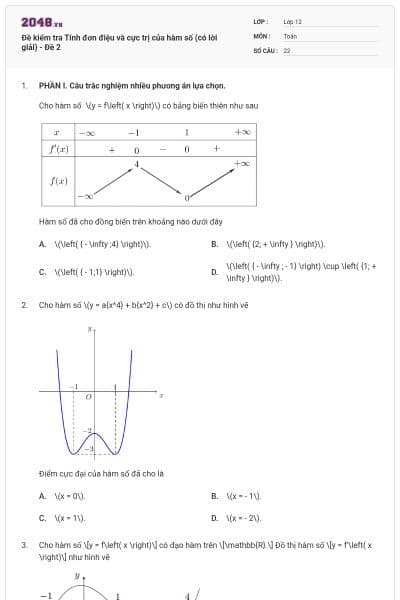
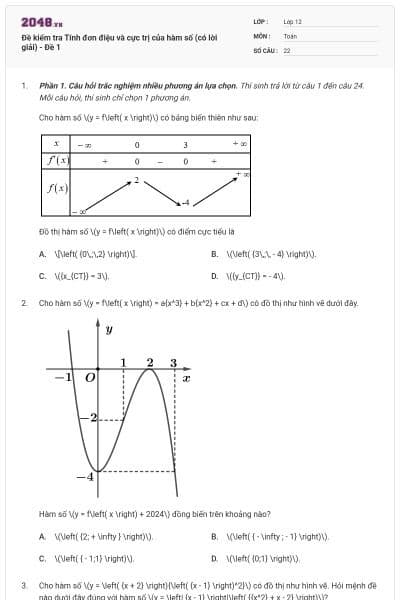
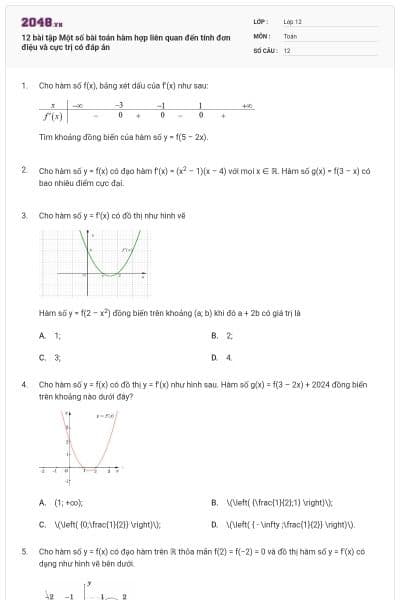
Đề kiểm tra Tính đơn điệu và cực trị của hàm số (có lời giải) - Đề 5
25 câu hỏi
PHẦN 1. Câu trắc nghiệm nhiều phương án lựa chọn.
Hàm số \(y = - {x^3} + 3x\) đồng biến trên khoảng nào dưới đây?
\(\left( { - 1\,;\,1} \right)\).
\(\left( { - \infty \,;\, - 1} \right)\).
\(\left( {0\,;\,\sqrt 3 } \right)\).
\(\left( {1\,;\, + \infty } \right)\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Hàm số đồng biến trên khoảng nào đưới đây?
\(\left( {0; + \infty } \right)\)
\(\left( { - 2;2} \right)\)
\(\left( { - 1;1} \right)\)
\(\left( { - 2;1} \right)\)
Cho hàm số\[y = f\left( x \right)\] có \[f'\left( x \right) = \left( {x + 2} \right)\left( {x + 1} \right)\left( {{x^2} - 1} \right)\]. Hàm số \[y = f\left( x \right)\] đồng biến trên khoảng nào sau đây?
\(\left( { - 1;1} \right)\).
\(\left( {0; + \infty } \right)\).
\(\left( { - \infty ; - 2} \right)\).
\(\left( { - 2; - 1} \right)\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
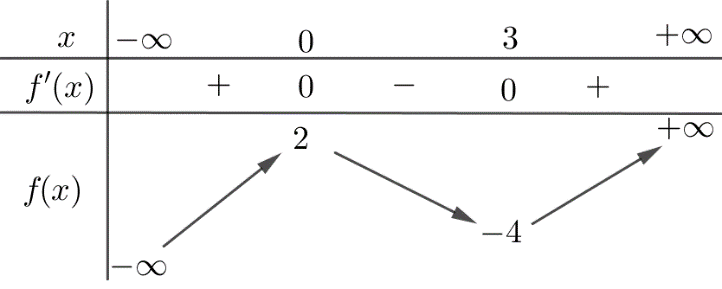
Giá trị cực tiểu của hàm số đã cho bằng
\[ - 4\].
\[3\].
\[0\].
\[2\].
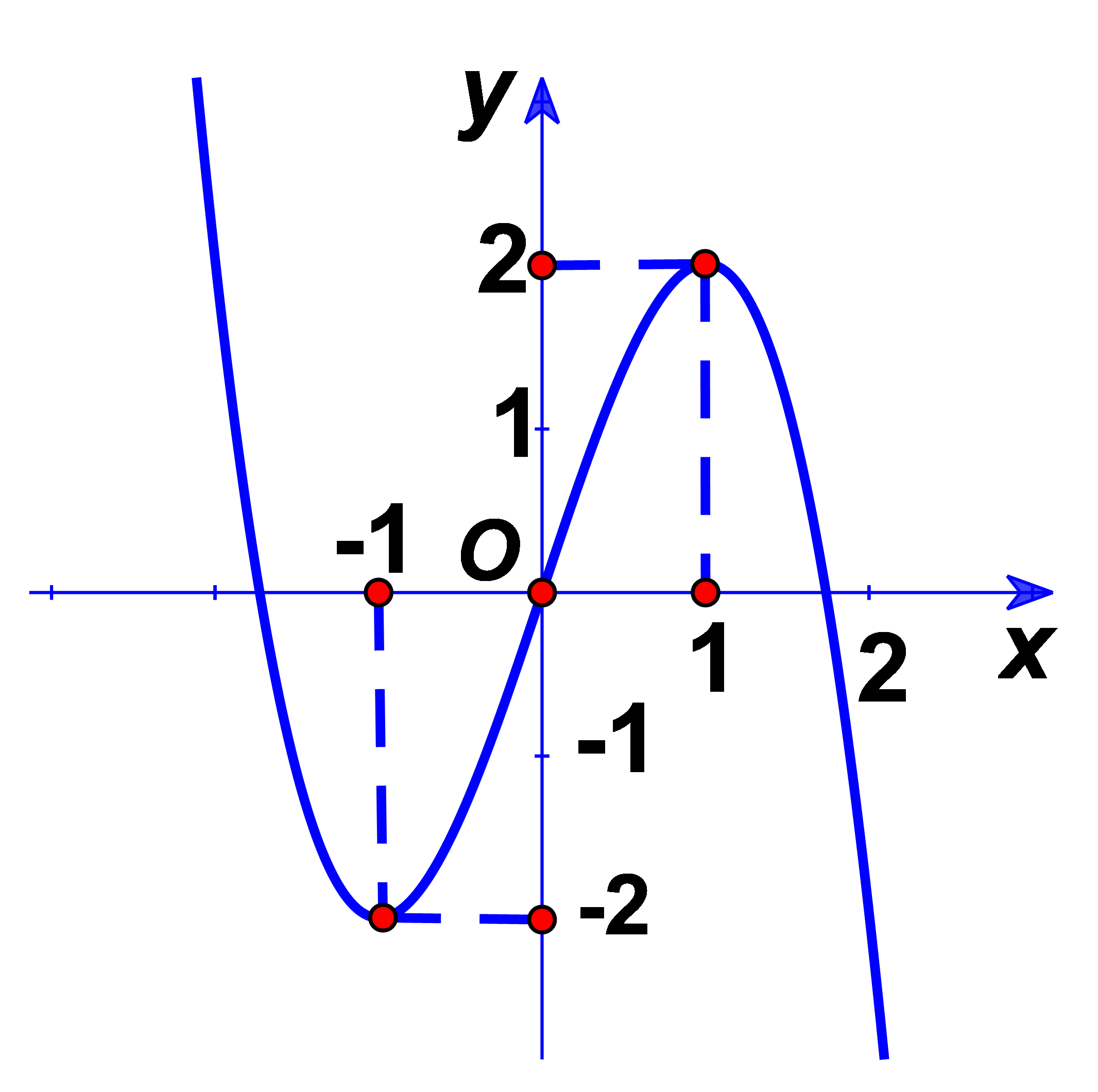
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ dưới đây:
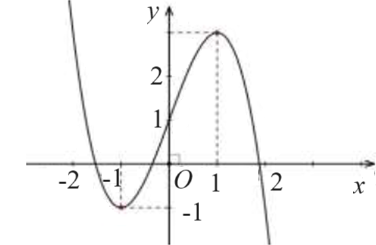
Hàm số \(y = f\left( x \right)\) đạt cực tiểu tại
\(x = 3\).
\(x = - 1\).
\(x = 1\).
\(x = 2\).
Trên đoạn \(\left[ { - 2;1} \right]\), hàm số \(y = {x^3} - 3{x^2} - 1\) đạt giá trị lớn nhất tại điểm.
\(x = - 2\).
\(x = 0\).
\(x = - 1\).
\(x = 1\).
Tìm giá trị nhỏ nhất của hàm số \[y = \frac{{{x^2} + 3}}{{x - 1}}\] trên đoạn \(\left[ {2;4} \right]\)
\[\mathop {\min }\limits_{\left[ {2;4} \right]} y = 6\]
\[\mathop {\min }\limits_{\left[ {2;4} \right]} y = - 2\]
\[\mathop {\min }\limits_{\left[ {2;4} \right]} y = - 3\]
\[\mathop {\min }\limits_{\left[ {2;4} \right]} y = \frac{{19}}{3}\]
Xét hàm số\[y = f\left( x \right)\] với \[x \in \left[ { - 1;5} \right]\]có bảng biến thiên như sau
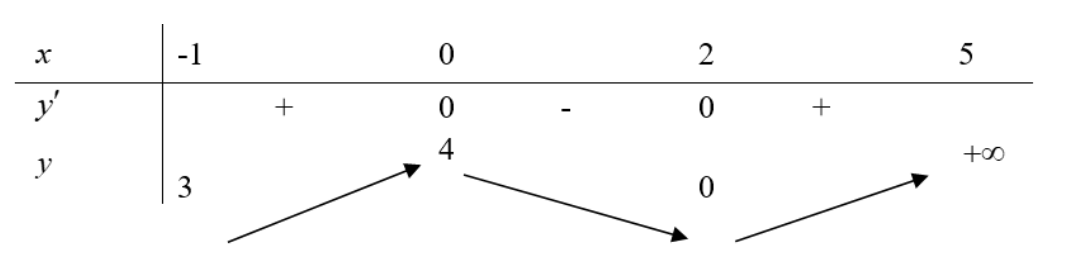
Khẳng định nào sau đây đúng?
Hàm số đã cho không tồn tại GTLN trên đoạn \(\left[ { - 1;5} \right]\).
Hàm số đã cho đạt GTNN tại \(x = - 1\)và \(x = 2\) trên đoạn \(\left[ { - 1;5} \right]\).
Hàm số đã cho đạt GTNN tại \(x = - 1\)và đạt GTLN tại \(x = 5\) trên đoạn \(\left[ { - 1;5} \right]\).
Hàm số đã cho đạt GTNN tại \(x = 0\) trên đoạn \(\left[ { - 1;5} \right]\).
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{3x + 1}}{{x - 1}}\) là:
\[y = \frac{1}{3}\].
\[y = 3\].
\[y = - 1\].
\[y = 1\].
Tiệm cận đứng của đồ thị hàm số \(y = \frac{{2x - 2}}{{x + 1}}\) là
\(x = - 2\).
\(x = 1\).
\(x = - 1\).
\(x = 2\).
Phương trình đường tiệm cận ngang của đồ thị hàm số \(y = x - \sqrt {{x^2} + 2x + 3} \) là
\(y = 1\).
\(y = 2\).
\(y = - 1\).
\(y = 0\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị như sau
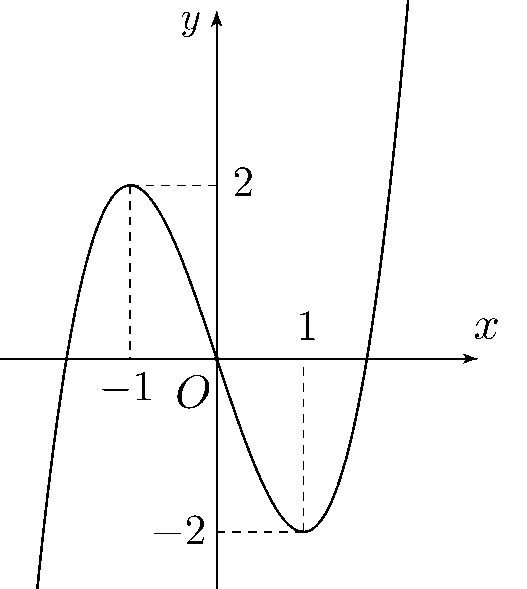
\(y = f\left( x \right)\) là hàm số nào trong các hàm số sau
\(y = - {x^3} + x\).
\(y = {x^3} - 3x\).
\(y = {x^4} - 2{x^2}\).
\(y = \frac{{x + 1}}{{x - 1}}\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị như sau
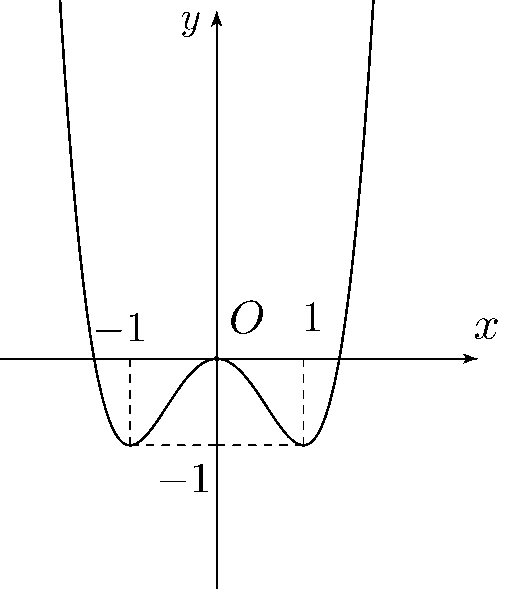
\(y = f\left( x \right)\) là hàm số nào trong các hàm số sau
\(y = - {x^4} + 2{x^2}\).
\(y = {x^3} - 3x\).
\(y = {x^4} - 2{x^2}\).
\(y = \frac{{x + 1}}{{x - 1}}\).
Đồ thị hàm số \(y = \frac{{{x^2} + x}}{{x - 1}}\) đi qua điểm nào trong các điểm sau
\(\left( {0;1} \right)\).
\(\left( { - 1;\frac{1}{2}} \right)\).
\(\left( {0;0} \right)\).
\(\left( {2;1} \right)\).
Độ giảm huyết áp của một bệnh nhân được cho bởi công thức \(f\left( x \right) = 0,025{x^2}\left( {30 - x} \right)\), trong đó \(x\) là liều lượng thuốc được tiêm cho bệnh nhân. Khi đó, liều lượng thuốc được tiêm cho bệnh nhân để huyết áp giảm nhiều nhất là
\(20\)miligam.
\(10\)miligam.
\(15\)miligam.
\(30\)miligam.
PHẦN 2. Câu trắc nghiệm đúng sai
Cho hàm số \(y = f\left( x \right)\) liên tục trên R và có bảng biến thiên như sau:
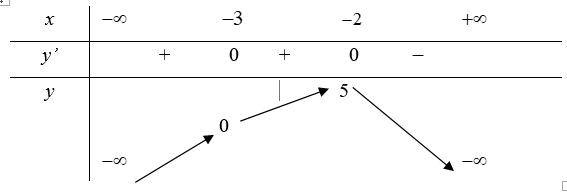
Khi đó:
a) Hàm số đã cho đồng biến trên các khoảng\(\left( { - \infty ; - 5} \right)\) và \(\left( { - 3; - 2} \right)\)
b) Hàm số đã cho đồng biến trên khoảng\(\left( { - \infty ;5} \right)\)
c) Hàm số đã cho nghịch biến trên khoảng\(\left( { - 2; + \infty } \right)\)
d) Hàm số đã cho đồng biến trên khoảng\(\left( { - \infty ; - 2} \right)\)
Cho hàm số \(y = \left( {m - 1} \right){x^4} - \left( {{m^2} - 2} \right){x^2} + 2\)(\(m\) là tham số). Khi đó:
a) Khi \(m = 0\) hàm số có 3 điểm cực trị
b) Khi \(m = 1\) đồ thị hàm số có điểm cực tiểu là \(M\left( {a;b} \right)\), khi đó \(a + b = 2\)
c)Với \[m = 2\] hàm số đạt cực đại tại \[x = - 1\].
d) Để hàm số đạt cực tiểu tại \(x = - 1\) thì \(m = k\), khi đó \({\log _k}8 = 2\)
Cho hàm số \[y = f\left( x \right)\]liên tục trên \[\mathbb{R}\] và có đạo hàm . Các mệnh đề sau đúng hay sai?
a) \(f\left( { - 2} \right) > \max \,\left\{ {f\left( { - 3} \right);\,f\left( 2 \right)} \right\}\).
b) \(f\left( { - 3} \right) < f\left( { - 2} \right) < f\left( 2 \right)\).
c) \(f\left( { - 2} \right) < \min \,\left\{ {f\left( { - 3} \right);\,f\left( 2 \right)} \right\}\).
d) \(f\left( { - 3} \right) > f\left( { - 2} \right) > f\left( 2 \right)\).
Cho hàm số \[y = \frac{{x + a}}{{bx + c}}\] với \[a,\,b,\,c \in \mathbb{Z}\] có đồ thị như hình vẽ dưới đây:
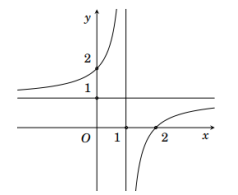
Các mệnh đề sau đúng hay sai?
a) Đồ thị hàm số có tiệm cận đứng \[x = 1\].
b) Đồ thị hàm số có tiện cận ngang \[y = 0\].
c) Hàm số đồng biến trên \[\mathbb{R}\].
d)\[T = a - 3b - 2c = - 3\].
PHẦN 3. Câu trắc nghiệm trả lời ngắnHàm số \(y = f\left( x \right) = {x^3} - 3x\)nghịch biến trên khoảng?
Giá trị cực đại của hàm số \[y = f\left( x \right) = {x^2}{e^{ - 2x}}\] bằng
Tìm giá trị nhỏ nhất \(m\) của hàm số \(y = {x^3} - 3{x^2} - 9x + 5\) trên đoạn \(\left[ { - 2;2} \right]\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau. Tìm tiệm cận đứng của đồ thị hàm số
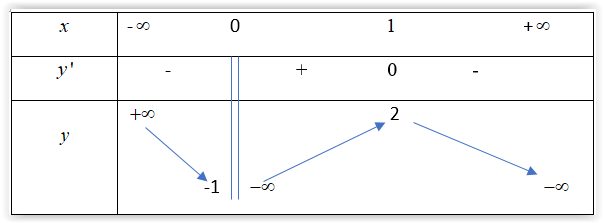
Cho hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\)có đồ thị là đường cong như hình vẽ.
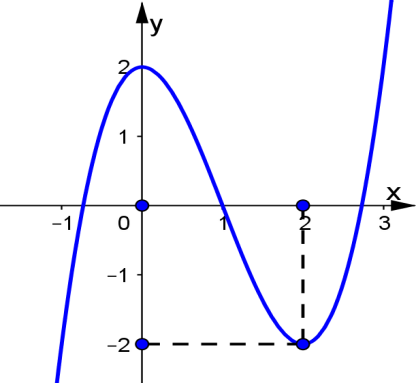
Tính tổng \(S = a + b + c + d\).
Một màn hình chữ nhật cao \(1,4{\rm{m}}\) và đặt ở độ cao \(1,8{\rm{m}}\) so với tầm mắt .
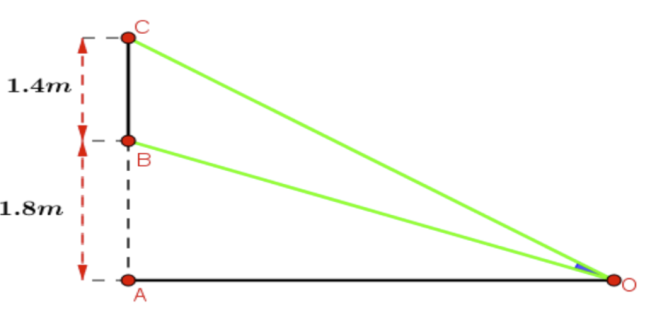
Để nhìn rõ nhất phải xác định vị trí đứng sao cho góc nhìn lớn nhất. Tính khoảng cách từ vị trí đó đến màn hình? Biết rằng góc \(\widehat {BOC}\) nhọn.