Đề kiểm tra Vectơ trong không gian (có lời giải) - Đề 5
22 câu hỏi
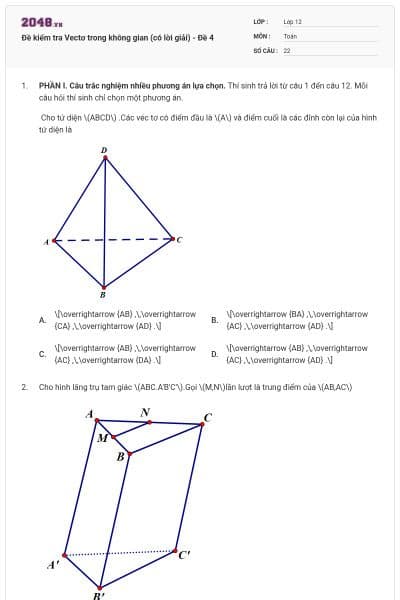
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Trong không gian cho vectơ \(\overrightarrow {AB} \). Khi đó:
Giá của vectơ\(\overrightarrow {AB} \)là\(\overrightarrow {AB} \).
Giá của vectơ\(\overrightarrow {AB} \)là \(\left| {\overrightarrow {AB} } \right|\).
Giá của vectơ\(\overrightarrow {AB} \) là đường thẳng \(AB\).
Giá của vectơ \(\overrightarrow {AB} \) là đoạn thẳng \(AB\).
Cho hình hộp chữ nhật \[ABCD.A'B'C'D'\]. Trong các vectơ dưới đây, vectơ nào cùng phương với vectơ\(\overrightarrow {AB} \)?
![Cho hình hộp chữ nhật \[ABCD.A'B'C'D'\]. Trong các vectơ dưới đây, vectơ nào cùng phương với vectơ \(\overrightarrow {AB} \)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/1-1759241026.png)
Vectơ\(\overrightarrow {AD} \).
Vectơ\(\overrightarrow {CC'} \).
Vectơ\(\overrightarrow {BD} \).
Vectơ\(\overrightarrow {CD} \).
Hình ảnh dưới đây là phân độ của 8 hướng trên la bàn. Mệnh đề nào sau đây sai?
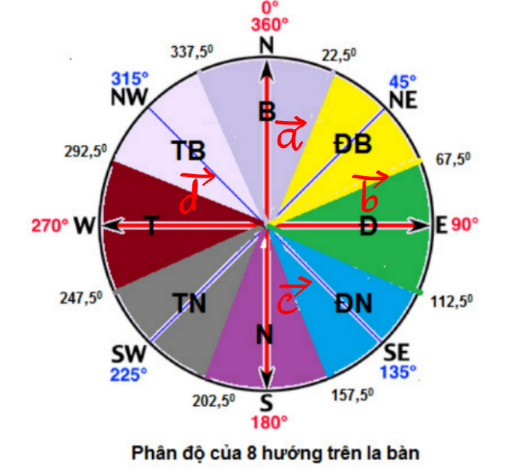
Hai vectơ \(\overrightarrow a \) và \(\overrightarrow c \) cùng phương.
Hai vectơ \(\overrightarrow a \) và \(\overrightarrow c \) ngược hướng.
Hai vectơ \(\overrightarrow b \) và \(\overrightarrow d \) cùng phương.
Hai vectơ \(\overrightarrow a \) và \(\overrightarrow c \) cùng hướng.
Cho hình hộp \[ABCD.A'B'C'D'\]. Vectơ \[\overrightarrow u = \overrightarrow {A'A} + \overrightarrow {A'B'} + \overrightarrow {A'D'} \] bằng vectơ nào dưới đây?
\(\overrightarrow {A'C} \).
\[\overrightarrow {CA'} \].
\[\overrightarrow {AC'} \].
\[\overrightarrow {C'A} \].
Cho hình lăng trụ tam giác \[ABC.A'B'C'\]. Đặt \[\overrightarrow {AA'} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b ,\overrightarrow {AC} = \overrightarrow c ,\overrightarrow {BC} = \overrightarrow d \]. Trong các biểu thức vec tơ sau đây, biểu thức nào là đúng?
\[\overrightarrow a = \overrightarrow b + \overrightarrow c \].
\[\overrightarrow a + \overrightarrow b + \overrightarrow c + \overrightarrow d = \overrightarrow 0 \].
\[\overrightarrow b - \overrightarrow c + \overrightarrow d = \overrightarrow 0 \].
\[\overrightarrow a + \overrightarrow b + \overrightarrow c = \overrightarrow d \].
Cho lập phương \[ABCD.A'B'C'D'\]có độ dài mỗi cạnh bằng 1. Tính độ dài của vectơ \[\overrightarrow {AC} + \overrightarrow {C'D'} \].
![Cho lập phương \[ABCD.A'B'C'D'\]có độ dài mỗi cạnh bằng 1. Tính độ dài của vectơ \[\overrightarrow {AC} + \overrightarrow {C'D'} \]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/5-1759241250.png)
\(\sqrt 3 \).
\(\sqrt 2 \).
\(1\).
\(2\sqrt 2 \).
Cho \(O\) là tâm hình bình hành \(ABCD\). Hỏi vectơ \(\left( {\overrightarrow {AO} - \overrightarrow {DO} } \right)\) bằng vectơ nào?
\(\overrightarrow {BA} \).
\(\overrightarrow {AD} \).
\(\overrightarrow {DC} \).
\(\overrightarrow {AC} \).
Cho ba điểm phân biệt \(A,B,C\). Nếu \(\overrightarrow {AB} = - 3\overrightarrow {AC} \) thì đẳng thức nào dưới đây đúng?
\(\overrightarrow {BC} = - 4\overrightarrow {AC} \)
\(\overrightarrow {BC} = - 2\overrightarrow {AC} \)
\(\overrightarrow {BC} = 2\overrightarrow {AC} \)
\(\overrightarrow {BC} = 4\overrightarrow {AC} \)
Cho tam giác \(ABC\) có điểm \(O\) thỏa mãn: \(\left| {\overrightarrow {OA} + \overrightarrow {OB} - 2\overrightarrow {OC} } \right| = \left| {\overrightarrow {OA} - \overrightarrow {OB} } \right|\). Khẳng định nào sau đây là đúng?
Tam giác \(ABC\) đều
Tam giác \(ABC\) cân tại \(C\)
Tam giác \(ABC\) vuông tại \(C\)
Tam giác \(ABC\) cân tại \(B\)
Cho hình hộp \[ABCD.A'B'C'D'\]. Đẳng thức nào dưới đây là đúng?
\(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AC} \).
\(\overrightarrow {AC'} = \overrightarrow {AA'} + \overrightarrow {AD} + \overrightarrow {AC} \).
\(\overrightarrow {AC'} = \overrightarrow {AB'} + \overrightarrow {AD} \).
\[\overrightarrow {AC'} = \overrightarrow {AC} + \overrightarrow {AB} + \overrightarrow {AA'} \].
Cho hình lập phương \[ABCD.A'B'C'D'\] cạnh bằng \[a\]. Tích vô hướng của hai vectơ \[\overrightarrow {DD'} \] và \[\overrightarrow {A'C'} \] bằng
\[\sqrt 2 {a^2}\].
\[{a^2}\].
\[ - \sqrt 2 {a^2}\].
\[0\].
Cho lập phươn g \[ABCD.A'B'C'D'\]có độ dài cạnh bằng \[a\]. Tính độ dài của vectơ \[\overrightarrow {AD'} + \overrightarrow {BA'} \].
![Cho lập phươn g \[ABCD.A'B'C'D'\]có độ dài cạnh bằng \[a\]. Tính độ dài của vectơ \[\overrightarrow {AD'} + \overrightarrow {BA'} \]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/9-1759241490.png)
\(\sqrt 3 a\).
\(\sqrt 2 a\).
\(\sqrt 6 a\).
\(2\sqrt 3 a\).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình chữ nhật. Biết rằng: cạnh \[AB = a\], \[AD = 2a\], cạnh bên \[SA = 2a\] và vuông góc với mặt đáy. Gọi \[M\], \[N\] lần lượt là trung điểm của các cạnh \[SB\], \[SD\]. Các mệnh đề sau đúng hay sai ?
a) Hai vectơ \[\overrightarrow {AB\,} \], \[\overrightarrow {CD\,} \] là hai vectơ cùng phương, cùng hướng.
b) Góc giữa hai vectơ \[\overrightarrow {SC\,} \] và \[\overrightarrow {AC\,} \] bằng \[60^\circ \].
c) Tích vô hướng \[\overrightarrow {AM\,} \cdot \,\overrightarrow {AB\,} = \frac{{{a^2}}}{2}\].
d) Độ dài của vectơ \[\overrightarrow {AM\,} - \overrightarrow {AN\,} \] là \[\frac{{a\sqrt 3 }}{2}\].
Cho hình lập phương \[ABCD.A\prime B\prime C\prime D\prime \] có cạnh bằng \[a\]. Trên các cạnh \[AA\prime \], \[CC\prime \] lần lượt lấy các điểm \[M\], \[N\] sao cho \[AM = \frac{2}{3}AA\prime \], \[CN = NC\prime \]. Các mệnh đề sau đúng hay sai ?
a) Góc giữa hai vectơ \[\overrightarrow {AN\,} \] và \[\overrightarrow {AC\,} \] bằng \[60^\circ \].
b) Độ dài của vectơ \[\overrightarrow {MN\,} + \overrightarrow {AM\,} \] là \[\frac{{3a}}{2}\].
c) Tích vô hướng \[\overrightarrow {AN\,} \cdot \,\overrightarrow {AC\,} = {a^2}\].
d) Tích vô hướng \[\overrightarrow {MN\,} \cdot \,\overrightarrow {A\prime C\prime \,} = 2{a^2}\].
Cho hình lăng trụ đứng \(ABC\,A'B'C'\) đáy là tam giác đều cạnh \(2a,\,AA' = a\sqrt 3 \). \(H,K\) lần lượt là trung điểm \(BC,\,\,B'C'\). Các mệnh đề sau đúng hay sai ?
a) Hai vectơ \[\overrightarrow {AH\,} \], \[\overrightarrow {KA'\,} \] là hai vectơ cùng phương, cùng hướng.
b) Góc giữa hai vectơ \[\overrightarrow {A'H\,} \] và \[\overrightarrow {AH\,} \] bằng \[60^\circ \].
c) Tích vô hướng \[\overrightarrow {AK\,} \cdot \,\overrightarrow {AB'\,} = \frac{{5{a^2}}}{2}\].
d) Độ dài của vectơ \[\overrightarrow {AK\,} + \overrightarrow {AH\,} \] là \[\frac{{a\sqrt 3 }}{2}\].
Cho tứ diện đều \(ABCD\) cạnh \(a\). \(E\) là điểm trên đoạn \(CD\) sao cho \(ED = 2CE\). Các mệnh đề sau đúng hay sai ?
a) Có \[6\] vectơ (khác vectơ \[\overrightarrow 0 \]) có điểm đầu và điểm cuối được tạo thành từ các đỉnh của tứ diện.
b) Góc giữa hai vectơ \[\overrightarrow {AB\,} \] và \[\overrightarrow {BC\,} \] bằng \[60^\circ \].
c) Nếu \[\overrightarrow {BE\,} = m\overrightarrow {BA\,} + n\overrightarrow {BC\,} + p\overrightarrow {BD\,} \] thì \[m + n + p = \frac{2}{3}\].
d) Tích vô hướng \(\overrightarrow {AD} .\overrightarrow {BE} = \frac{{{a^2}}}{6}\).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Cho tứ diện \[ABCD\]. Trên các cạnh \[AD\] và \[BC\] lần lượt lấy \[M,N\]sao cho \(AM = 3MD\), \(BN = 3NC\). Gọi \[P,Q\] lần lượt là trung điểm của \[AD\] và \[BC\]. Phân tích vectơ \(\overrightarrow {MN} \) theo hai vectơ \(\overrightarrow {PQ} \) và \(\overrightarrow {DC} \) ta được \[\overrightarrow {MN} = a\overrightarrow {PQ} + b\overrightarrow {DC} \] . Tính \[a + 2b\].
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình bình hành. Một mặt phẳng \[\left( \alpha \right)\] cắt các cạnh \[SA,\,\,SB,\,\,SC,\,SD\] lần lượt tại \[A',B',C',D'\]. Giá trị của biểu thức \[P = \frac{{SA}}{{SA'}} + \frac{{SC}}{{SC'}} - \frac{{SB}}{{SB'}} - \frac{{SD}}{{SD'}}\]bằng bao nhiêu ?
Cho hình lập phương\[ABCD.A'B'C'D'\] có cạnh bằng \[2\]. Tính \(\overrightarrow {AB} .\overrightarrow {A'C'} \).
![Cho hình lập phương \[ABCD.A'B'C'D'\] có cạnh bằng \[2\]. Tính \(\overrightarrow {AB} .\overrightarrow {A'C'} \). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/17-1759241886.png)
Cho tứ diện \[ABCD\], gọi \[M\], \[N\]lần lượt là trung điểm của \[BC\] và \[AD\], biết \(AB = a\), \(CD = a\), \(MN = \frac{{a\sqrt 3 }}{2}\). Tìm số đo góc giữa hai đường thẳng \[AB\] và \[CD\].
Cho hình lập phương \[B'C\] có đường chéo \[A'C = \frac{3}{{16}}\]. Gọi \(O\) là tâm hình vuông \(ABCD\) và điểm \[20\] thỏa mãn: \[\overrightarrow {OS} = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} + \overrightarrow {OA'} + \overrightarrow {OB'} + \overrightarrow {OC'} + \overrightarrow {OD'} \]. Khi đó độ dài của đoạn \[OS\] bằng \(\frac{{a\sqrt 3 }}{b}\) với \(a,b \in \mathbb{N}\) và \(\frac{a}{b}\) là phân số tối giản. Tính giá trị của biểu thức \(P = {a^2} + {b^2}\).
Khi chuyển động trong không gian, máy bay luôn chịu tác động của 4 lực chính: lực đẩy của động cơ, lực cản của không khí, trọng lực và lực nâng khí động học(hình ảnh 2.20).

Lực cản của không khí ngược hướng với lực đẩy của động cơ và có độ lớn tỉ lệ thuận với bình phương vận tốc máy bay. Một chiếc máy bay tăng vận tốc từ 900(km/h) lên 920(km/h), trong quá trình tăng tốc máy bay giữ nguyên hướng bay. Lực cản của không khí khi máy bay đạt vận tốc 900(km/h) và 920(km/h) lần lượt biểu diễn bởi hai véc tơ \[\overrightarrow {{F_1}} \]và \[\overrightarrow {{F_2}} \] với \[\overrightarrow {{F_1}} = k\overrightarrow {{F_2}} \,\,(k \in \mathbb{R};k > 0)\]. Tính giá trị của \[k\](làm tròn kết quả đến chữ số thập phân thứ hai).