Đề kiểm tra Vectơ trong không gian (có lời giải) - Đề 4
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho tứ diện \(ABCD\) .Các véc tơ có điểm đầu là \(A\) và điểm cuối là các đỉnh còn lại của hình tứ diện là
![PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án. Câu 1. [1] Cho tứ diện \(ABCD\) .Các véc tơ có điểm đầu là \(A\) và điểm cuối là các đỉnh còn lại của hình tứ diện là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/1-1759239860.png)
\[\overrightarrow {AB} ,\,\overrightarrow {CA} ,\,\overrightarrow {AD} .\]
\[\overrightarrow {BA} ,\,\overrightarrow {AC} ,\,\overrightarrow {AD} .\]
\[\overrightarrow {AB} ,\,\overrightarrow {AC} ,\,\overrightarrow {DA} .\]
\[\overrightarrow {AB} ,\,\overrightarrow {AC} ,\,\overrightarrow {AD} .\]
Cho hình lăng trụ tam giác \(ABC.A'B'C'\).Gọi \(M,N\)lần lượt là trung điểm của \(AB,AC\)
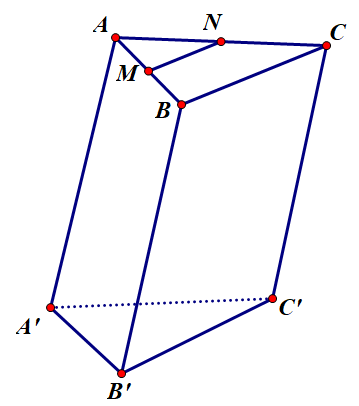
Trong 4 véc tơ \(\overrightarrow {AB} \,,\,\overrightarrow {CB} \,,\overrightarrow {B'C'} ,\overrightarrow {A'C'} \) véc tơ nào cùng hướng với véc tơ \(\overrightarrow {MN} \)
\(\overrightarrow {AB} \).
\(\overrightarrow {CB} \).
\(\overrightarrow {B'C} '\).
\(\overrightarrow {A'C'} \).
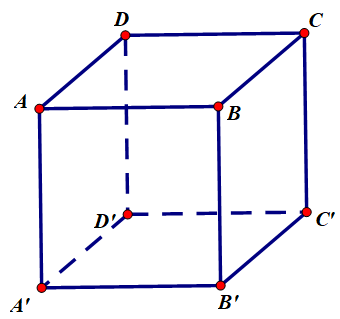
Cho hình hộp \(ABCD.A'B'C'D'\) .Số các véc tơ có điểm đầu, điểm cuối là các đỉnh của hình hộp và bằng véc tơ \(\overrightarrow {AB} \) là
1
2
3
4
Cho hình hộp \(ABCD.A'B'C'D'\). Trong các khẳng định dưới đây, đâu là khẳng định đúng?
\(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = \overrightarrow {AC'} \).
\(\overrightarrow {AB} + \overrightarrow {AA'} + \overrightarrow {AD} = \overrightarrow {AC'} \).
\(\overrightarrow {AB} + \overrightarrow {AA'} + \overrightarrow {AD} = \overrightarrow {AC} \).
\(\overrightarrow {AB} + \overrightarrow {AA'} + \overrightarrow {AD} = \overrightarrow 0 \).
Trong không gian cho tam giác \(ABC\) có \(G\) là trọng tâm và điểm \(M\) nằm ngoài mặt phẳng \(\left( {ABC} \right)\). Khẳng định nào sau đây là đúng?
\(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \).
\(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = 0\).
\(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow {MG} \).
\(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \).
Cho hình chóp đều \(S.ABCD\) tất cả các cạnh bằng \(2\sqrt 3 \) (đvđd). Tính độ dài vectơ \(\overrightarrow u = \overrightarrow {SA} - \overrightarrow {SC} \)
\(\sqrt 3 \).
\(\sqrt 2 \).
\(2\sqrt 6 \).
\(2\sqrt 2 \).
Cho tứ diện \(ABCD\). Mệnh đề nào dưới đây là mệnh đề đúng?
\(\overrightarrow {BC} - \overrightarrow {BA} = \overrightarrow {DA} - \overrightarrow {DC} \).
\(\overrightarrow {AC} - \overrightarrow {AD} = \overrightarrow {BD} - \overrightarrow {BC} \).
\(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {DB} - \overrightarrow {DC} \).
\(\overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {CD} - \overrightarrow {CB} \).
Cho hình lăng trụ \(ABC.A'B'C'\), \(M\) là trung điểm của \(BB'\). Đặt \(\overrightarrow {CA} = \vec a\), \(\overrightarrow {CB} = \vec b\), \(\overrightarrow {AA'} = \vec c\). Khẳng định nào sau đây đúng?
\(\overrightarrow {AM} = \vec b + \vec c - \frac{1}{2}\vec a\).
\(\overrightarrow {AM} = \vec a - \vec c + \frac{1}{2}\vec b\).
\(\overrightarrow {AM} = \vec a + \vec c - \frac{1}{2}\vec b\).
\(\overrightarrow {AM} = \vec b - \vec a + \frac{1}{2}\vec c\).
Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh \(a\). Tính độ dài véctơ \(\overrightarrow x = \overrightarrow {A'C'} - \overrightarrow {A'A} \) theo \(a\)?
\(a\sqrt 2 \).
\(\frac{{a\sqrt 3 }}{2}\).
\(a\sqrt 6 \).
\(a\sqrt 3 \).
Cho tứ diện \(S.ABC\) có \(M,N,P\) là trung điểm của \(SA,SB,SC\). Tìm khẳng định đúng?
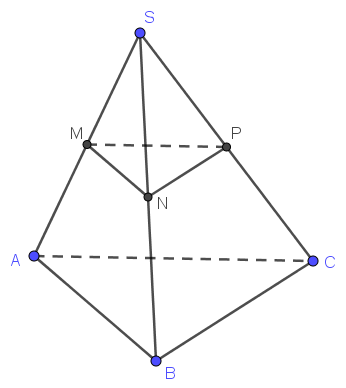
\[\overrightarrow {AB} = \frac{1}{2}\left( {\overrightarrow {PN} - \overrightarrow {PM} } \right)\].
\[\overrightarrow {AB} = \overrightarrow {PN} - \overrightarrow {PM} \].
\[\overrightarrow {AB} = 2\left( {\overrightarrow {PM} - \overrightarrow {PN} } \right)\].
\[\overrightarrow {AB} = 2\left( {\overrightarrow {PN} - \overrightarrow {PM} } \right)\].
Cho tứ diện \(S.ABC\) có đáy là tam giác đều cạnh \(a\), \(SB\) vuông góc với đáy và \(SB = \sqrt 3 a\). Góc giữa hai vectơ \(\left( {\overrightarrow {AB} ,\overrightarrow {AS} } \right)\) là
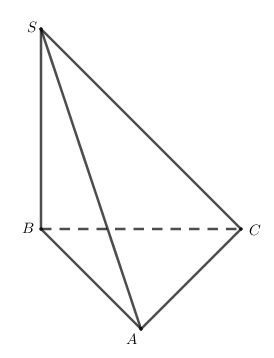
\[{60^o}\].
\[{30^o}\].
\[{45^o}\].
\[{90^o}\].
Cho hình chóp \(S.ABC\) có \(AB = 4,\widehat {BAC} = {60^o},\overrightarrow {AB} .\overrightarrow {AC} = 6\). Khi đó độ dài \(\overrightarrow {AC} \)là
\[3\].
\[6\].
\[4\].
\[12\].
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho tứ diện \(ABCD\) có \(AB = AC = AD = a\) và \[\widehat {BAC} = \widehat {BAD} = 60^\circ ,\,\widehat {CAD} = 90^\circ \]. Gọi \(I\) là điểm trên cạnh \(AB\) sao cho \(AI = 3IB\) và \(J\) là trung điểm của \(CD\). Gọi \[\alpha \] là góc giữa hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {IJ} \).
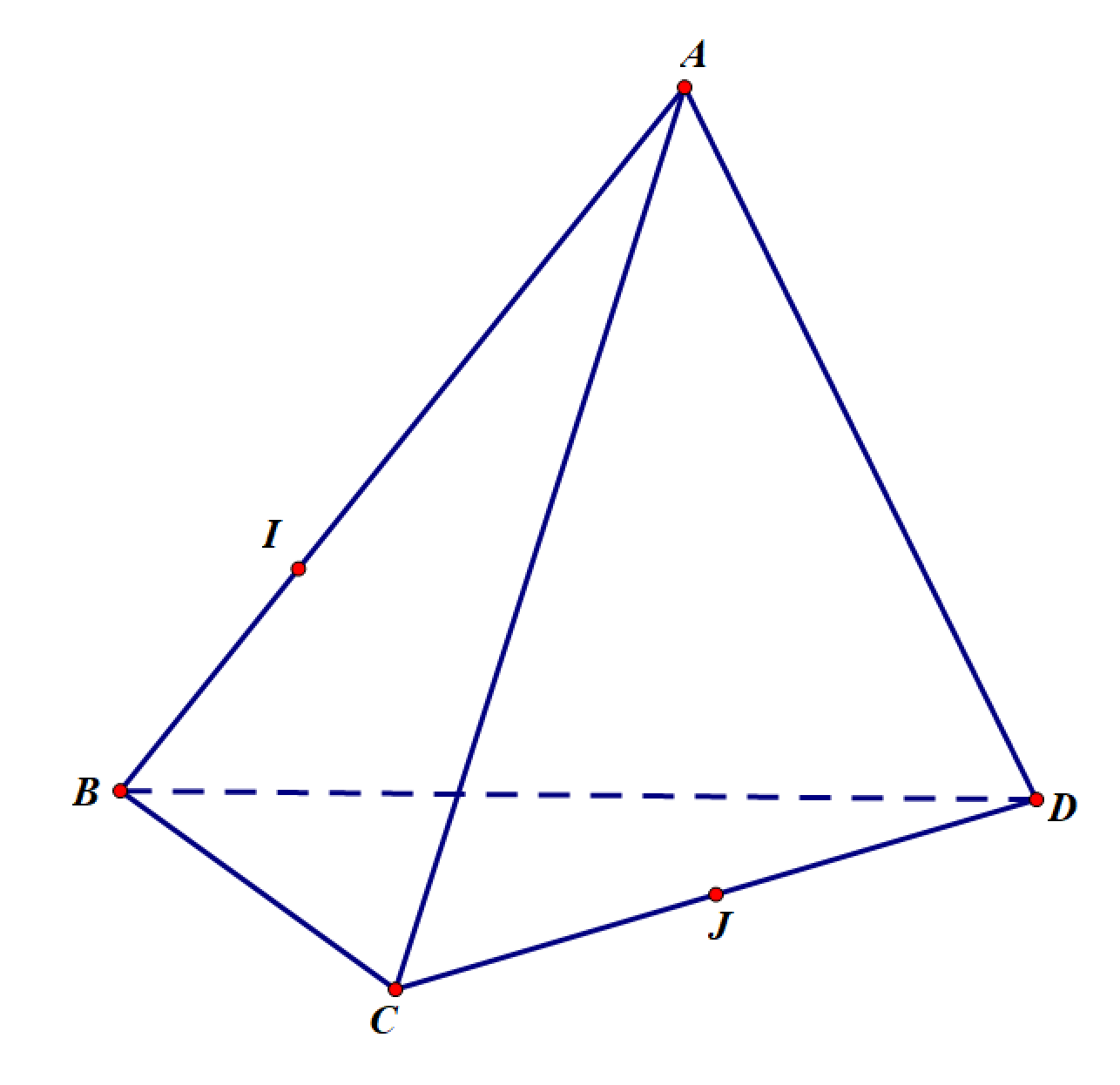
a) Tam giác \(BCD\) vuông cân
b)\(\overrightarrow {IJ} = \frac{1}{2}\overrightarrow {AC} + \frac{1}{2}\overrightarrow {AD} + \frac{3}{2}\overrightarrow {AB} \)
c)\[\overrightarrow {AB} .\overrightarrow {AC} + \overrightarrow {AC} .\overrightarrow {AD} + \overrightarrow {AD} .\overrightarrow {AB} = \frac{{{a^2}}}{2}\]
d)\[\cos \alpha = - \frac{{\sqrt 5 }}{5}\]
Cho tứ diện \(ABCD\). Gọi \(M\), \(N\), \(P\), \(Q\), \(R\), \(S\), \(G\) lần lượt là trung điểm các đoạn thẳng \(AB\), \(CD\), \(AC\), \(BD\), \(AD\), \(BC\), \(MN\).
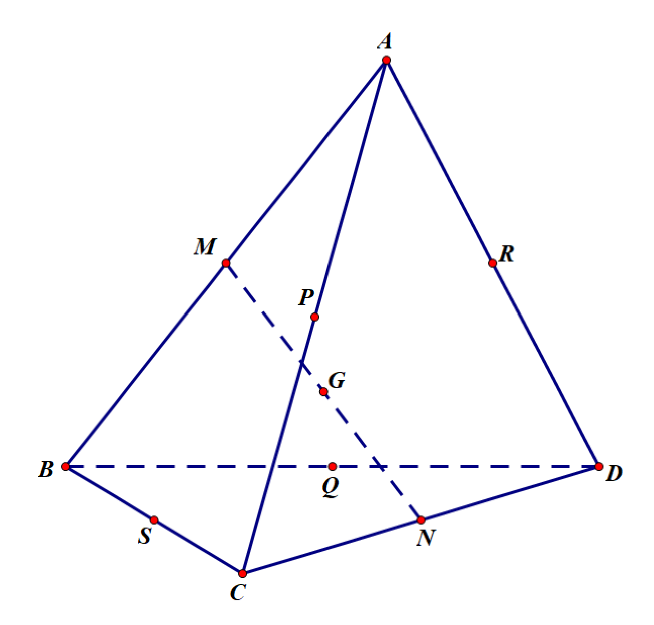
a) \(\overrightarrow {MR} = \overrightarrow {SN} \).
b) \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \).
c) \(2\overrightarrow {PQ} = \overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} \).
d) \(\left| {\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} } \right|\) nhỏ nhất khi và chỉ khi điểm \(I\) trùng với điểm \(G\).
Cho hình hộp chữ nhật \[ABCD.EFGH\] có \[AB = AE = 2\], \[AD = 3\] và đặt \[\overrightarrow a = \overrightarrow {AB} ,\,\overrightarrow b = \overrightarrow {AD} ,\,\overrightarrow c = \overrightarrow {AE} \]. Lấy điểm \[M\] thỏa \[\overrightarrow {AM} = \frac{1}{5}\overrightarrow {AD} \] và điểm \[N\] thỏa \[\overrightarrow {EN} = \frac{2}{5}\overrightarrow {EC} \]. (tham khảo hình vẽ)
![Khi đó ta có a) \[\overrightarrow {MA} = - \frac{1}{5}\overrightarrow b \]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/13-1759240659.png)
Khi đó ta có
a) \[\overrightarrow {MA} = - \frac{1}{5}\overrightarrow b \].
b) \[\overrightarrow {EN} = \frac{2}{5}\left( {\overrightarrow a - \overrightarrow b + \overrightarrow c } \right)\].
c) \[{\left( {m.\overrightarrow a + n.\overrightarrow b + n.\overrightarrow c } \right)^2} = {m^2}.{\overrightarrow a ^2} + {n^2}.{\overrightarrow b ^2} + {p^2}.{\overrightarrow c ^2}\] với \[m,\,n,\,p\] là các số thực.
d) \[MN = \frac{{\sqrt {61} }}{5}\].
Cho hình lăng trụ tam giác đều \[ABC.{A_1}{B_1}{C_1}\] có cạnh đáy bằng \[x\] và chiều cao bằng \[y\]. (tham khảo hình vẽ)
![Cho hình lăng trụ tam giác đều \[ABC.{A_1}{B_1}{C_1}\] có cạnh đáy bằng \[x\] và chiều cao bằng \[y\]. (tham khảo hình vẽ) (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/14-1759240699.png)
Khi đó ta có
a) \[\overrightarrow {AB} .\overrightarrow {AC} = \frac{1}{2}{x^2}\].
b) \[\overrightarrow {A{C_1}} = \overrightarrow {AC} + \overrightarrow {A{A_1}} \].
c) \[\overrightarrow {C{B_1}} = \overrightarrow {AB} - \overrightarrow {CA} + \overrightarrow {A{A_1}} \].
d) Góc \[\left( {A{C_1},\,C{B_1}} \right) > 60^\circ \] khi \[\frac{y}{x} < \sqrt 2 \].
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 3.
Cho hình lăng trụ \(ABC.A'B'C'.\) Đặt \(\overrightarrow {AB} = \vec a,\,\,\overrightarrow {AA'} = \vec b,\,\,\overrightarrow {AC} = \vec c.\) Ta biểu diễn \(\overrightarrow {B'C} = m\overrightarrow a + n\overrightarrow b + p\overrightarrow c \), khi đó \(m + n + p\) bằng bao nhiêu ?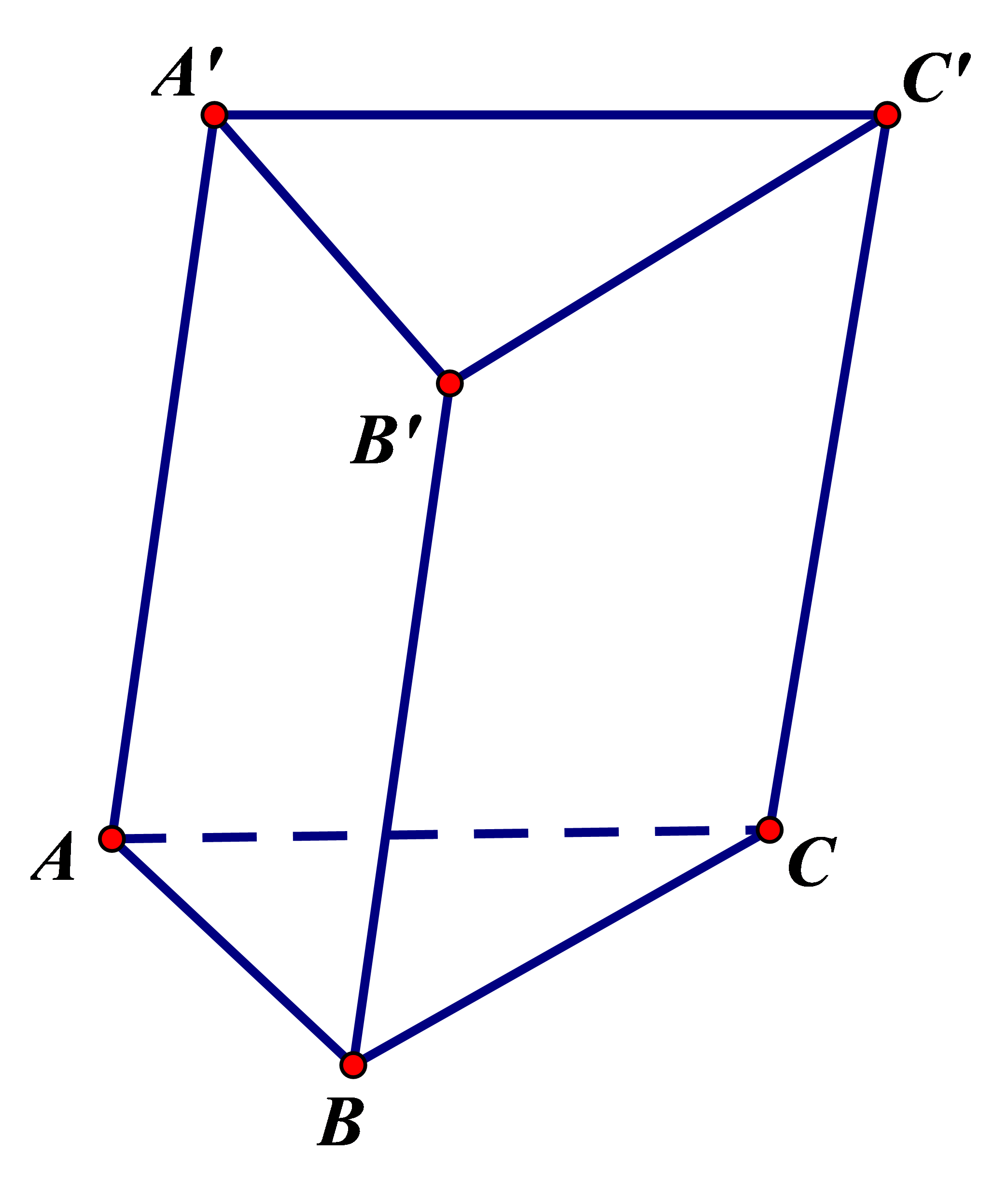
Cho tứ diện\(ABCD\), gọi \(I\),\(J\) lần lượt là trung điểm của \(AB\) và \(CD\).
1) \[\overrightarrow {IJ} \, = \,\frac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {BD} } \right)\].
2) \[\overrightarrow {IJ} \, = \,\frac{1}{2}\left( {\overrightarrow {AD} + \overrightarrow {BC} } \right)\].
3) \[\overrightarrow {IJ} \, = \,\frac{1}{2}\left( {\overrightarrow {DC} + \overrightarrow {AD} + \overrightarrow {BD} } \right)\].
4) \[\overrightarrow {IJ} \, = \,\frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {CD} } \right)\].
Trong các đẳng thức trên có bao nhiêu đẳng thức đúng?
Cho tứ diện đều \[ABCD\] có cạnh bằng \[4\]. Giá trị tích vô hướng \[\overrightarrow {AB} \left( {\overrightarrow {AB} - \overrightarrow {CA} } \right)\] bằng
Trong không gian, cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) có cùng độ dài bằng \(6\). Biết độ dài của vectơ \(\overrightarrow a + 2\overrightarrow b \) bằng \(6\sqrt 3 \). Biết số đo góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) là \(x\) độ. Giá trị của \(x\) là bao nhiêu?
Cho tứ diện đều \(ABCD\) có cạnh bằng \(15\). Biết độ dài của \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} \) bằng \(a\sqrt 6 \), khi đó giá trị của \(a\) là?
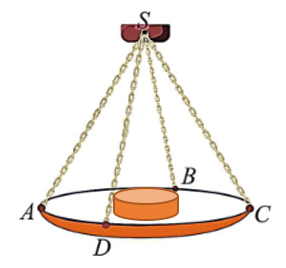
Một chiếc cân đòn tay đang cân một vật có khối lượng \(m = 3\,{\rm{kg}}\)được thiết kế với đĩa cân được giữ bởi bốn đoạn xích \(SA\,,\,SB\,,\,SC\,,\,SD\) sao cho \(S.ABCD\) là hình chóp tứ giác đều có \(\widehat {ASC} = 90^\circ \). Biết độ lớn của lực căng cho mỗi sợi xích có dạng \(\frac{{a\sqrt 2 }}{4}\). Lấy \(g = 10\,{\rm{m/}}{{\rm{s}}^{\rm{2}}}\), khi đó giá trị của \[a\] bằng bao nhiêu?