20 câu trắc nghiệm Toán 12 Kết nối tri thức Bài 6. Vectơ trong không gian (Đúng sai - Trả lời ngắn) có đáp án
20 câu hỏi
Cho hình hộp ABCD.A'B'C'D'. Vectơ nào sau đây cùng phương với vectơ \(\overrightarrow {AB} \)?
\(\overrightarrow {A'D'} \).
\(\overrightarrow {AC} \).
\(\overrightarrow {CD} \).
\(\overrightarrow {BA'} \).
Cho hình hộp ABCD.A'B'C'D'. Vectơ \(\overrightarrow {BA} \) bằng với vectơ nào sau đây?
\(\overrightarrow {A'B'} \).
\(\overrightarrow {CD} \).
\(\overrightarrow {BC} \).
\(\overrightarrow {AB} \).
Cho hình chóp S.ABC. Mệnh đề nào sau đây đúng?
\(\overrightarrow {SA} - \overrightarrow {AB} = \overrightarrow {SB} \).
\(\overrightarrow {SA} - \overrightarrow {SB} = \overrightarrow {AB} \).
\(\overrightarrow {SA} - \overrightarrow {SB} = \overrightarrow {BA} \).
\(\overrightarrow {SA} - \overrightarrow {SB} = \overrightarrow {SC} \).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Tính tổng \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} \).
\(2\overrightarrow {SO} \).
\(4\overrightarrow {SO} \).
\(3\overrightarrow {SO} \).
\(\overrightarrow 0 \).
Cho hình hộp ABCD.A'B'C'D'. Tính tổng \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {A'C'} \).
\(2\overrightarrow {AA'} \).
\(\overrightarrow 0 \).
\(2\overrightarrow {AC} \).
\(2\overrightarrow {C'A'} \).
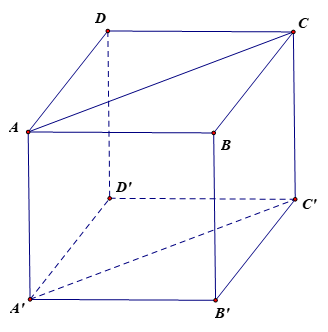
Cho hình lập phương ABCD.A'B'C'D'. Hãy xác định góc giữa cặp vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {A'C'} \).
90°.
\(60^\circ \).
45°.
120°.
Cho hình lăng trụ ABC.A'B'C' có E là trung điểm của BB', biết \(\overrightarrow {AE} = m\overrightarrow {AA'} + n\overrightarrow {CA} + p\overrightarrow {CB} \). Giá trị của 2m – n + p bằng bao nhiêu?
3.
1.
2.
\(\frac{1}{2}\).
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) thỏa mãn \(\left| {\overrightarrow a } \right| = 3;\left| {\overrightarrow b } \right| = 2\) và \(\overrightarrow a .\overrightarrow b = - 3\). Xác định góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \).
α = 30°.
α = 45°.
α = 60°.
α = 120°.
Cho hình lập phương ABCD.A'B'C'D'. Góc giữa hai vectơ \(\overrightarrow {AC} ,\overrightarrow {DA'} \) bằng
30°.
45°.
60°.
120°.
Cho hình chóp S.ABC có SA = SB = SC và \(\widehat {ASB} = \widehat {BSC} = \widehat {CSA}\). Hãy xác định góc giữa cặp vectơ \(\overrightarrow {SA} \) và \(\overrightarrow {BC} \)?
90°.
45°.
60°.
120°.
Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB, CD và G là trung điểm MN.
(a) \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \).
(b) \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MG} \).
(c) \(\overrightarrow {MN} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {CD} } \right)\).
(d)\(2\overrightarrow {MN} = \overrightarrow {AC} + \overrightarrow {BD} \).
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi I là tâm hình vuông ABCD. gọi G là trọng tâm của tam giác AB'C.
(a) \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \).
(b) \(\overrightarrow {GA} + \overrightarrow {GB'} + \overrightarrow {GC} = 2\overrightarrow {GI} \).
(c) \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {A'C'} \).
(d)\(\overrightarrow {BD'} = 2\overrightarrow {BG} \).
Cho hình chóp S.ABCD có SA vuông góc với đáy, SA = a, ABCD là hình chữ nhật với AB = a, AD = 2a và M là trung điểm của CD. Khi đó:
(a)\(\overrightarrow {SB} - \overrightarrow {MB} - \overrightarrow {SC} - \overrightarrow {SD} = \overrightarrow 0 \).
(b)\(\cos \left( {\overrightarrow {SA} ,\overrightarrow {SM} } \right) = \frac{{2\sqrt {21} }}{{21}}\).
(c)\(\left| {\overrightarrow {AM} - \overrightarrow {SA} } \right| = a\sqrt {21} \).
(d)\(\overrightarrow {SM} .\overrightarrow {AB} = \frac{1}{2}{a^2}\).
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a; \(AD = a\sqrt 3 \); AA' = 2a. Khi đó:
(a) \(\overrightarrow {AB'} + \overrightarrow {CD'} = \overrightarrow 0 \).
(b) \(\overrightarrow {A'D} + \overrightarrow {CB'} = \overrightarrow 0 \).
(c)\(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = a\sqrt 5 \).
(d) \(\left| {\overrightarrow {AB} + \overrightarrow {A'D'} + \overrightarrow {CC'} } \right| = 2a\sqrt 2 \).
Trong không gian, cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi G là điểm thỏa mãn \(\overrightarrow {GS} + \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \)(tham khảo hình vẽ)
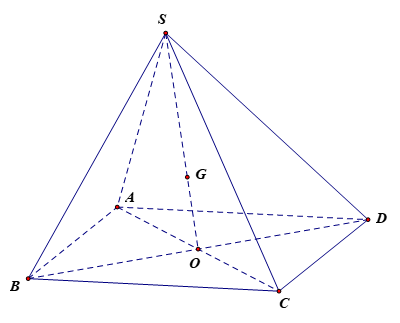
(a) Hai vectơ \(\overrightarrow {AO} ;\overrightarrow {CO} \) bằng nhau.
(b)\(\overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} \).
(c)\(\overrightarrow {GS} = 4\overrightarrow {OG} \).
(d) Nếu tam giác ABC có AB = 2a; \(BC = a\sqrt 7 \); AC = 3a thì \(\overrightarrow {AB} .\overrightarrow {AC} = 3{a^2}\).
Cho tứ diện đều ABCD có cạnh bằng 8 và M là trung điểm CD. Tính \(\overrightarrow {AB} .\overrightarrow {AM} \).
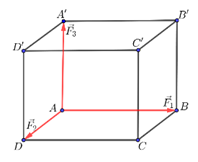
Cho hình hộp chữ nhật ABCD.A'B'C'D' như hình vẽ. Đặt một vật tại đỉnh A, khi đó tác động vào vật bởi những lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) có giá trị lần lượt nằm trên các cạnh AB, AD, AA' và \(\left| {\overrightarrow {{F_1}} } \right| = 2N,\left| {\overrightarrow {{F_2}} } \right| = 3N,\left| {{F_3}} \right| = 4N\). Hãy xác định độ lớn của hợp lực \(\overrightarrow F \) tác động lên vật (làm tròn đến hàng phần trăm).
Có ba lực cùng tác động vào một vật. Hai trong ba lực này hợp với nhau một góc 100° và có độ lớn lần lượt là 25 N và 12 N. Lực thứ ba vuông góc với mặt phẳng tạo bởi hai lực đã cho và có độ lớn 4 N. Tính độ lớn của hợp lực của ba lực trên (làm tròn kết quả đến hàng đơn vị).
Nếu một vật có khối lượng m(kg) thì lực hấp dẫn \(\overrightarrow P \) của Trái Đất tác dụng lên vật được xác định theo công thức \(\overrightarrow P = m\overrightarrow g \), trong đó \(\overrightarrow g \) là gia tốc rơi tự do có độ lớn g = 9,8 m/s2. Tính độ lớn của lực hấp dẫn của Trái Đất tác dụng lên một quả táo có khối lượng 105 gam (làm tròn kết quả đến hàng phần trăm).
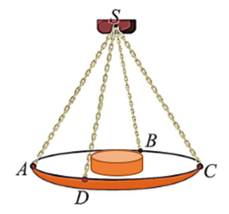
Một chiếc cân đòn tay đang cân một vật có khối lượng \(m = 3\,{\rm{kg}}\)được thiết kế với đĩa cân được giữ bởi bốn đoạn xích \(SA\,,\,SB\,,\,SC\,,\,SD\) sao cho \(S.ABCD\) là hình chóp tứ giác đều có \(\widehat {ASC} = 90^\circ \). Biết độ lớn của lực căng cho mỗi sợi xích có dạng \(\frac{{a\sqrt 2 }}{4}\). Lấy \(g = 10\,{\rm{m/}}{{\rm{s}}^{\rm{2}}}\), khi đó giá trị của \[a\] bằng bao nhiêu?
