Đề kiểm tra Vectơ trong không gian (có lời giải) - Đề 2
22 câu hỏi
PHẦN 1: CÂU HỎI TRẮC NGHIỆM
Trong không gian, cho hình hộp \(ABCD\,A'B\,'C'D'\). Vectơ đối của vectơ \[\overrightarrow {AA'} \]là
\[\overrightarrow {A'C'} \].
\[\overrightarrow {BA'} \].
\[\overrightarrow {BB'} \].
\[\overrightarrow {C'C} \].
Trong không gian, cho tứ diện \(ABCD\). Ta có \[\overrightarrow {AB} \, + \,\overrightarrow {CD} \]bằng
\[\overrightarrow {AD} \, + \,\overrightarrow {BC} \].
\[\overrightarrow {DA} \, + \,\overrightarrow {CB} \].
\[\overrightarrow {DA} \, + \,\overrightarrow {BC} \].
\[\overrightarrow {AD} \, + \,\overrightarrow {CB} \].
Trong không gian, cho hình lập phương \(ABCD\,A'B\,'C'D'\). Góc giữa hai vectơ \(\overrightarrow {BD} \,,\,\overrightarrow {B'C} \)bằng
\(30^\circ \).
\(45^\circ \).
\(60^\circ \).
\(90^\circ \).
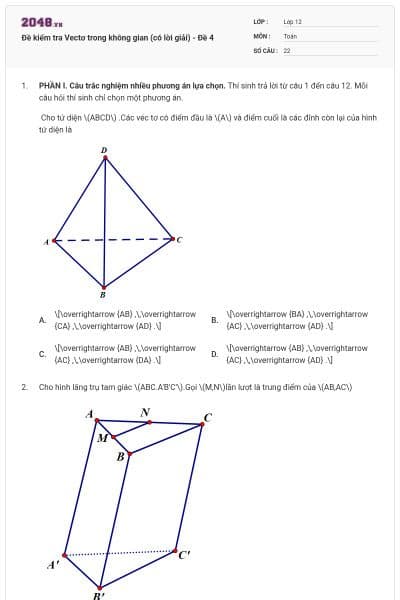
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\)(tham khảo hình vẽ dưới). Khẳng định nào dưới đây đúng?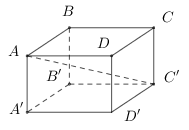
\(\overrightarrow {AC'} = \overrightarrow {BD'} \).
\(\overrightarrow {AD} \)cùng hướng với \(\overrightarrow {B'C'} \).
\(\overrightarrow {CD} \)cùng hướng với \(\overrightarrow {D'C'} \).
\(\overrightarrow {AC'} \)cùng phương với \(\overrightarrow {A'C'} \).
Cho \(\left| {\overrightarrow a } \right| = 2;\;\left| {\overrightarrow b } \right| = 6\), góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) bằng \(120^\circ \). Khẳng định nào dưới đây đúng?
\(\overrightarrow a .\overrightarrow b = 12\).
\[\overrightarrow a .\overrightarrow b = 40\].
\[\overrightarrow a .\overrightarrow b = - 6\].
\[\overrightarrow a .\overrightarrow b = 6\sqrt 3 \].
Cho hình hộp \[ABCD.A'B'C'D'\]. Gọi \[O\]là tâm của hình hộp, khẳng định nào dưới đây đúng?
\[\overrightarrow {OA} + \overrightarrow {OA'} = \overrightarrow 0 \]
\[\overrightarrow {OA} + \overrightarrow {OC'} = \overrightarrow 0 \]
\[\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow 0 \]
\[\overrightarrow {OA} + \overrightarrow {OD} = \overrightarrow 0 \]
Cho hình lăng trụ tam giác \(ABC.A'B'C'\). Đặt \(\overrightarrow {AA'} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b ,\overrightarrow {AC} = \overrightarrow c \). Khi đó biểu diến \(\overrightarrow {BC'} \) theo các véc tơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \)
\(\overrightarrow {BC'} = - \overrightarrow a + \overrightarrow b + \overrightarrow c \).
\(\overrightarrow {BC'} = \overrightarrow a - \overrightarrow b + \overrightarrow c \).
\(\overrightarrow {BC'} = \overrightarrow a + \overrightarrow b + \overrightarrow c \).
\(\overrightarrow {BC'} = \overrightarrow a + \overrightarrow b - \overrightarrow c \).
Cho \(\Delta ABC\) có \(AB = AC = 5a\) và \(\widehat {BAC} = 120^\circ \). Độ dài của vectơ tổng \(\overrightarrow {AB} + \overrightarrow {AC} \) bằng
\(10a\).
\(\frac{{5a\sqrt 3 }}{2}\).
\(5a\).
\(5a\sqrt 3 \).
Cho tứ diện \(ABCD\) có trọng tâm \(G\), gọi \(M\) là trung điểm \(AD\), khi đó:
\(\overrightarrow {MG} = \frac{1}{4}\left( {\overrightarrow {MA} + \overrightarrow {MD} } \right)\).
\(\overrightarrow {MG} = \frac{1}{4}\left( {\overrightarrow {MC} + \overrightarrow {MB} } \right)\).
\(\overrightarrow {MG} = \frac{1}{4}\left( {\overrightarrow {MC} + \overrightarrow {MD} } \right)\).
\(\overrightarrow {MG} = \frac{1}{4}\left( {\overrightarrow {MC} - \overrightarrow {MD} } \right)\).
Cho hình hộp \[ABCD.{A_1}{B_1}{C_1}{D_1}\]. Chọn đẳng thức sai?
\(\overrightarrow {BC} + \overrightarrow {BA} = \overrightarrow {{B_1}{C_1}} + \overrightarrow {{B_1}{A_1}} \).
\(\overrightarrow {AD} + \overrightarrow {{D_1}{C_1}} + \overrightarrow {{D_1}{A_1}} = \overrightarrow {DC} \).
\(\overrightarrow {BC} + \overrightarrow {BA} + \overrightarrow {B{B_1}} = \overrightarrow {B{D_1}} \).
\(\overrightarrow {BA} + \overrightarrow {D{D_1}} + \overrightarrow {B{D_1}} = \overrightarrow {BC} \).
Cho tứ diện \[ABCD\]. Gọi \[G\] là trọng tâm tam giác \[ABC.\] Tìm giá trị của \[k\] thích hợp điền vào đẳng thức vectơ: \[\overrightarrow {DA} + \overrightarrow {DB} + \overrightarrow {DC} = k\overrightarrow {DG} \]
\(k = \frac{1}{3}\).
\[k = 2.\]
\[k = 3.\]
\(k = \frac{1}{2}\).
Cho hình hộp \(ABCD.A'B'C'D'\). Tìm giá trị của \(k\) thích hợp điền vào đẳng thức vectơ: \[\overrightarrow {AC} + \overrightarrow {BA'} + k\left( {\overrightarrow {DB} + \overrightarrow {C'D} } \right) = \overrightarrow 0 \].
\(k = 0\).
\[k = 1.\]
\[k = 4\].
\(k = 2\).
PHẦN 2: CÂU TRẮC NGHIỆM ĐÚNG SAI
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông,\(SA\)vuông góc với mặt phẳng \((ABCD)\).Gọi \[I,J\] lần lượt là trung điểm của \[SA,SC\]. \[G\]là trọng tâm tam giác \[SBD\]
![Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông,\(SA\)vuông góc với mặt phẳng \((ABCD)\).Gọi \[I,J\] lần lượt là trung điểm của \[SA,SC\]. \[G\]là trọng tâm tam giác \[SBD\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/1-1759238082.png)
a) \(\overrightarrow {AC} - \overrightarrow {AB} = \overrightarrow {AD} \).
b) \(\overrightarrow {AS} + \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AG} \).
c) \[\overrightarrow {{\rm{IJ}}} .\overrightarrow {BD} = \overrightarrow 0 \]
d) \({\overrightarrow {AG} ^2} = {\overrightarrow {AS} ^2} + {\overrightarrow {AB} ^2} + {\overrightarrow {AD} ^2}\).
Cho hình lập phương \(ABCD.A'B'C'D'\). Gọi \(G\) là trọng tâm tam giác \(B'C'D'\), \(I\) là trung điểm của \(AB'\) .
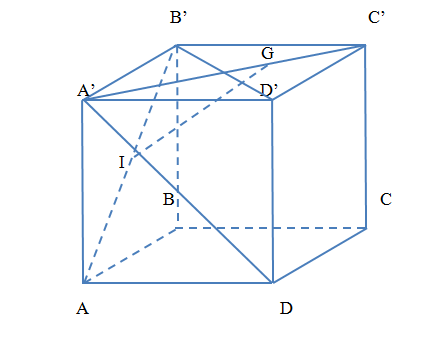
a) \(\overrightarrow {A'D} = \overrightarrow {AA'} - \overrightarrow {AD} \).
b) \(\overrightarrow {GB'} + \overrightarrow {GA} = \overrightarrow {GB} + \overrightarrow {GA'} \).
c) \[6\overrightarrow {IG} = 3\overrightarrow {AA'} + \overrightarrow {AB} + 4\overrightarrow {AD} \;.\]
d) \[cos\left( {\overrightarrow {A'D} \,,\,\overrightarrow {IG} } \right) = \frac{{\sqrt {13} }}{{26}}.\].
Cho tứ diện \[ABCD\]. Các điểm \(M,\;N,\;I\) lần lượt là trung điểm của \(AB\), \(CD\), \(MN\) và \(G\) là trọng tâm tam giác \(BCD\). Xét tính đúng sai của các mệnh đề sau:
a) \[\overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MN} \].
b) \[\overrightarrow {AD} + \overrightarrow {BC} = 2\overrightarrow {MN} \].
c) \[\overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} = 3\overrightarrow {IG} \].
d) \(2\overrightarrow {IG} + \overrightarrow {IA} = \overrightarrow 0 \).
Cho tam giác \(ABC\) với \(M,{\rm{ }}N,{\rm{ }}P\) lần lượt là trung điểm các cạnh \(AB,{\rm{ }}BC,{\rm{ }}CA\). Xét tính đúng sai các mệnh đề sau
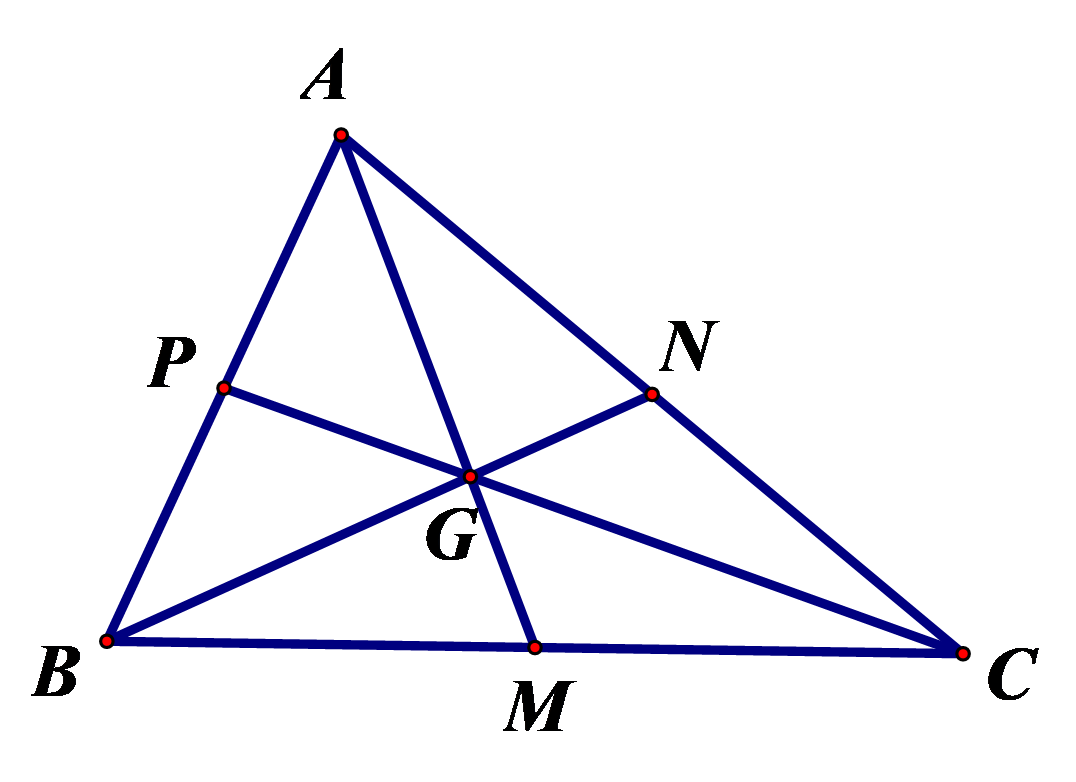
a) \(\overrightarrow {BM} + \overrightarrow {CN} = \overrightarrow {MN} \).
b) \(\overrightarrow {PA} + \overrightarrow {BM} + \overrightarrow {CN} = \vec 0\).
c) \(\overrightarrow {AN} = \overrightarrow {AM} + \overrightarrow {AP} \).
d) \(\overrightarrow {AM} + \overrightarrow {BN} + \overrightarrow {CP} = \overrightarrow 0 \).
PHẦN 3: CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN
Cho hai vectơ \(\overrightarrow a ,\overrightarrow b \) vuông góc với nhau và \(\overrightarrow {\left| a \right|} = 6,\left| {\overrightarrow b } \right| = 4\). Tính \(\left( {\overrightarrow a - \overrightarrow b } \right)\left( {2\overrightarrow a + \overrightarrow b } \right)\)
Cho hình hộp \(ABCD.A'B'C'D'\)có tất cả các mặt đều là hình thoi cạnh \[\sqrt 6 \] và các góc \(\widehat {BAA'} = \widehat {BAD} = \widehat {DAA'} = {60^0}\). Tính độ dài \(AC'\)
Cho hình chóp \[O.ABC\] có ba cạnh \[OA\], \[OB\], \[OC\] đôi một vuông góc và \[OA = OB = OC = a\]. Gọi \[M\] là trung điểm cạnh \[AB\]. Tính góc tạo bởi hai vectơ \[\overrightarrow {AC} \] và \[\overrightarrow {OM} \] ?
Theo định luật II Newton (Vật lí 10 - Chân trời sáng tạo, Nhà xuất bản Giáo dục Việt Nam, 2023, trang 60): Gia tốc của một vật có cùng hướng với lực tác dụng lên vật. Độ lớn của gia tốc tỉ lệ thuận với độ lớn của lực và tỉ lệ nghịch với khối lượng của vật:
\(\vec F = m\vec a\)
trong đó \(\vec a\) là vectơ gia tốc \(\left( {{\rm{m}}/{{\rm{s}}^2}} \right),\vec F\) là vectơ lực (N)

Hình 20 tác dụng lên vật, \(m\left( {{\rm{\;kg}}} \right)\) là khối lượng của vật.
Muốn truyền cho quả bóng có khối lượng \(0,5{\rm{\;kg}}\) một gia tốc \(50{\rm{\;m}}/{{\rm{s}}^2}\) thì cần một lực đá có độ lớn là bao nhiêu?
Môt chiếc khinh khí cầu bay lên từ địa điểm cho trước. Sau khoảng thời gian bay, chiếc khinh khí cầu cách địa điểm xuất phát \(2,5km\) về hướng nam và \(1,7km\) về hướng đông, đồng thời cách mặt đất là \(0,6km\). Chọn hệ trục toạ độ \(Oxyz\) với gốc \(O\) đặt tại điểm xuất phát của chiếc khinh khí cầu, mặt phẳng \(\left( {Oxy} \right)\) trùng với mặt đất, trục \(Ox\) hướng về nam, trục \(Oy\) hướng về phía đông và trục \(Oz\) hướng thẳng đứng lên trời, đơn vị đo lấy theo kilomet.
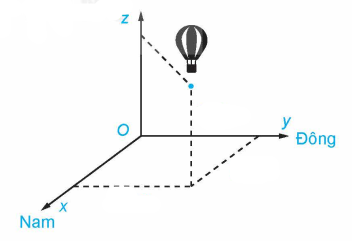
Tính khoảng cách từ địa điểm xuất phát đến địa điểm hiện tại của khinh khí cầu (đơn vị lấy theo kilomet và làm tròn đến \(2\) chữ số sau phần thập phân)
Một chiếc đèn tròn được treo song song với mặt phẳng nằm ngang bởi ba sợi dây không dãn xuất phát từ điểm \[O\] trên trần nhà lần lượt buộc vào ba điểm \[A,B,C\] trên đèn tròn sao cho tam giác \[ABC\] đều. Độ dài của ba đoạn dây \[OA,OB,OC\] đều bằng \[L\]. Trọng lượng của chiếc đèn là \[27N\] và bán kính của chiếc đèn là \(0,5m\).

Tìm chiều dài tối thiểu của mỗi sợi dây, biết rằng mỗi sợi dây đó được thiết kế để chịu được lực căng tối đa là \(12N\). (Chiều dài tính theo đơn vị cm và làm tròn đến 1 số sau phần thập phân)