10 bài tập Sử dụng phép toán tổng, hiệu hai vectơ và tích của một vectơ với một số để chứng minh, phân tích các vectơ có lời giải
10 câu hỏi
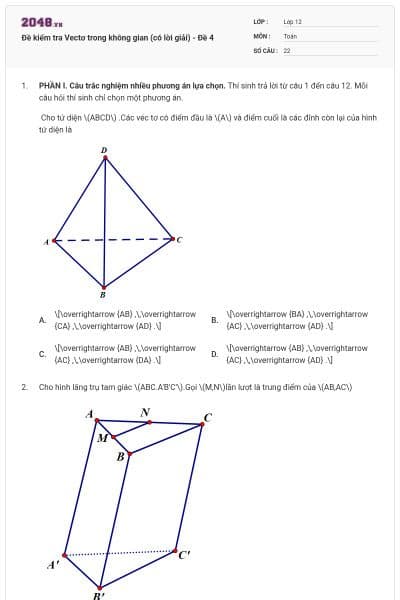
Cho hình tứ diện ABCD có trọng tâm G. Mệnh đề nào sau đây sai?
\[\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \];
\[\overrightarrow {OG} = \frac{1}{4}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} } \right)\];
\[\overrightarrow {AG} = \frac{2}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right)\];
\[\overrightarrow {AG} = \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right)\].
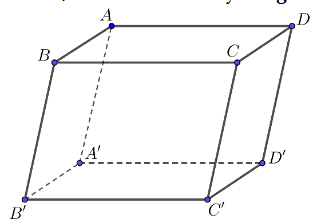
Cho hình hộp ABCD.A'B'C'D'. Mệnh đề nào sau đây đúng?
\[\overrightarrow {AB} + \overrightarrow {A'D'} = \overrightarrow {AC} \];
\[\overrightarrow {AB} + \overrightarrow {A'D'} = \overrightarrow {BD} \];
\[\overrightarrow {AB} + \overrightarrow {A'D'} = \overrightarrow {AC'} \];
\[\overrightarrow {AB} + \overrightarrow {A'D'} = \overrightarrow {CA} \].
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AD và BC. Tổng \(\overrightarrow {AB} + \overrightarrow {DC} \) bằng
\[\overrightarrow 0 \];
\[2\overrightarrow {AD} \];
\[2\overrightarrow {MN} \];
\[2\overrightarrow {NM} \].
Cho hình lăng trụ tam giác ABC.A'B'C'. Đặt \(\overrightarrow {AA'} = \overrightarrow a ;\overrightarrow {AB} = \overrightarrow b ;\overrightarrow {AC} = \overrightarrow c ;\overrightarrow {BC} = \overrightarrow d \). Trong các biểu thức vectơ sau đây, biểu thức nào đúng?
\[\overrightarrow a + \overrightarrow b + \overrightarrow c = \overrightarrow d \];
\[\overrightarrow a = \overrightarrow b + \overrightarrow c \];
\[\overrightarrow a + \overrightarrow b + \overrightarrow c + \overrightarrow d = \overrightarrow 0 \];
\[\overrightarrow b - \overrightarrow c + \overrightarrow d = \overrightarrow 0 \].
Cho tứ diện ABCD có trọng tâm G, gọi M là trung điểm AD. Khi đó:
\[\overrightarrow {MG} = \frac{1}{4}\left( {\overrightarrow {MA} + \overrightarrow {MD} } \right)\];
\[\overrightarrow {MG} = \frac{1}{4}\left( {\overrightarrow {MC} + \overrightarrow {MB} } \right)\];
\[\overrightarrow {MG} = \frac{1}{4}\left( {\overrightarrow {MC} + \overrightarrow {MD} } \right)\];
\[\overrightarrow {MG} = \frac{1}{4}\left( {\overrightarrow {MC} - \overrightarrow {MD} } \right)\].
Cho tứ diện ABCD. Gọi M và P lần lượt là trung điểm của các cạnh AB và CD. Đặt \(\overrightarrow {AB} = \overrightarrow b ;\overrightarrow {AC} = \overrightarrow c ;\overrightarrow {AD} = \overrightarrow d \). Khẳng định nào sau đây đúng?
\[\overrightarrow {MP} = \frac{1}{2}\left( {\overrightarrow c + \overrightarrow d + \overrightarrow b } \right)\];
\[\overrightarrow {MP} = \frac{1}{2}\left( {\overrightarrow d + \overrightarrow b - \overrightarrow c } \right)\];
\[\overrightarrow {MP} = \frac{1}{2}\left( {\overrightarrow c + \overrightarrow b - \overrightarrow d } \right)\];
\[\overrightarrow {MP} = \frac{1}{2}\left( {\overrightarrow c + \overrightarrow d - \overrightarrow b } \right)\].
Cho hình lăng trụ ABC.A'B'C'. Đặt \(\overrightarrow {AA'} = \overrightarrow a ;\overrightarrow {AB} = \overrightarrow b ;\overrightarrow {AC} = \overrightarrow c \). Gọi G' là trọng tâm của tam giác A'B'C'. Vectơ \(\overrightarrow {AG'} \) bằng?
\[\frac{1}{3}\left( {\overrightarrow a + 3\overrightarrow b + \overrightarrow c } \right)\];
\[\frac{1}{3}\left( {3\overrightarrow a + \overrightarrow b + \overrightarrow c } \right)\];
\[\frac{1}{3}\left( {\overrightarrow a + \overrightarrow b + 3\overrightarrow c } \right)\];
\[\frac{1}{3}\left( {\overrightarrow a + \overrightarrow b + \overrightarrow c } \right)\].
Cho hình lập phương ABCD.A'B'C'D'. Gọi O là tâm của hình lập phương. Khẳng định nào sau đây là đúng?
\[\overrightarrow {AO} = \frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\];
\[\overrightarrow {AO} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\];
\[\overrightarrow {AO} = \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\];
\[\overrightarrow {AO} = \frac{2}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\].
Cho tứ diện ABCD. Điểm N xác định bởi đẳng thức sau \(\overrightarrow {AN} = \overrightarrow {AB} + \overrightarrow {AC} - \overrightarrow {AD} \). Mệnh đề nào đúng?
N là trung điểm BD;
N là đỉnh hình bình hành BCDN;
N là đỉnh hình bình hành CDBN;
N ≡ A.
Cho tứ diện S.ABC có M, N, P là trung điểm của SA, SB, SC. Tìm khẳng định đúng?
\[\overrightarrow {AB} = \frac{1}{2}\left( {\overrightarrow {PN} - \overrightarrow {PM} } \right)\];
\[\overrightarrow {AB} = \overrightarrow {PN} - \overrightarrow {PM} \];
\[\overrightarrow {AB} = 2\left( {\overrightarrow {PM} - \overrightarrow {PN} } \right)\];
\[\overrightarrow {AB} = 2\left( {\overrightarrow {PN} - \overrightarrow {PM} } \right)\].