Đề kiểm tra Vectơ trong không gian (có lời giải) - Đề 1
22 câu hỏi
PHẦN 1: CÂU HỎI TRẮC NGHIỆM
Trong không gian cho 3 điểm \[M,{\rm{ }}N,{\rm{ }}P\] phân biệt. Tính \(\overrightarrow {PM} + \overrightarrow {MN} \).
\[\overrightarrow {NM} \].
\[\overrightarrow {MN} \].
\[\overrightarrow {NP} \].
\[\overrightarrow {PN} \].
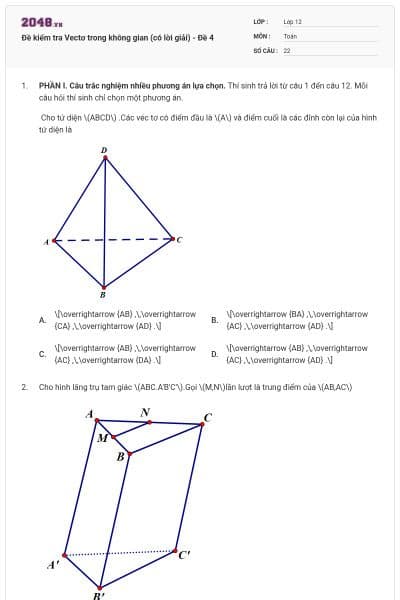
Cho hình lập phương \[ABCD.A'B'C'D'\]. Vectơ có điểm đầu và điểm cuối là các đỉnh của hình lập phương \[ABCD.A'B'C'D'\] và bằng vectơ \(\overrightarrow {AD} \) là
![Cho hình lập phương \[ABCD.A'B'C'D'\]. Vectơ có điểm đầu và điểm cuối là các đỉnh của hình lập phương \[ABCD.A'B'C'D'\] và bằng vectơ \(\overrightarrow {AD} \) là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/1-1759236578.png)
\[\overrightarrow {B'C'} \].
\[\overrightarrow {DA} \].
\[\overrightarrow {CB} \].
\[\overrightarrow {AB} \].
Gọi \(I\)là trung điểm của\(AB\). Khẳng định nào sau đây sai?
\(\overrightarrow {IA} + \overrightarrow {IB} = \overrightarrow 0 \).
\[IA = IB\].
\(\overrightarrow {IA} = \overrightarrow {IB} \).
\(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \).
Cho hình hộp \[ABCD.EFGH\]. Kết quả quả phép toán \[\overrightarrow {AB} - \overrightarrow {EH} \]là
![Cho hình hộp \[ABCD.EFGH\]. Kết quả quả phép toán \[\overrightarrow {AB} - \overrightarrow {EH} \] là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/3-1759236661.png)
\[\overrightarrow {BD} \].
\[\overrightarrow {AE} \].
\[\overrightarrow {DB} \].
\[\overrightarrow {BH} \].
Cho hai vectơ \[\overrightarrow u ,\overrightarrow v \] có \[\left| {\overrightarrow u } \right| = 3,\left| {\overrightarrow v } \right| = 4\] và góc giữa hai vectơ \[\overrightarrow u ,\overrightarrow v \] bằng \[{60^o}\]. Tích vô hướng \[\overrightarrow u .\overrightarrow v \] bằng
\[12\].
\[6\].
\[ - 12\].
\[ - 6\].
Trong không gian, cho 3 điểm \[A,\;B,\;C\] phân biệt. Hiệu hai véc tơ \(\overrightarrow {AB} - \overrightarrow {AC} \) bằng
\[\overrightarrow {CB} .\]
\[\overrightarrow {BC} \].
\[\overrightarrow {BA} \].
\[\overrightarrow {CA} \].
Cho hình hình hộp\[ABCD.A'B'C'D'\], có đáy \[ABCD\] hình bình hành tâm \(O\). Khi đó \[2.\overrightarrow {AO} \] bằng véc tơ nào sau đây?
\[\overrightarrow {AC} \].
\[\overrightarrow {AD} \].
\[\overrightarrow {A'C} \].
\[\overrightarrow {AB} \].
Cho biết \[G\] là trọng tâm của tứ diện \[ABCD\], mệnh đề nào sau đây đúng?
\[GA = GB = GC = GD\].
\[\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \]
\[\overrightarrow {GA} - \overrightarrow {GB} = \overrightarrow {GC} - \overrightarrow {GD} \]
\[GA + GB + GC + GD = 0\]
Cho hình lập phương\[ABCD.A'B'C'D'\] có độ dài cạnh là \(a\). Khi đó \[\overrightarrow {AB} .\overrightarrow {AD} \] bằng
\[{a^2}\].
\(0.\)
\[a\].
\[\frac{{{a^2}}}{2}\].
Do \[AB \bot AD\] nên \[\left( {\overrightarrow {AB} \overrightarrow {,AD} } \right) = 90^\circ \] nên \[\overrightarrow {AB} .\overrightarrow {AD} \]=\(0\)
\[\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \].
\[\overrightarrow {AB} = \overrightarrow {D'C'} \].
\[\overrightarrow {AB} + \overrightarrow {AA'} = \overrightarrow {AD} + \overrightarrow {DD'} .\]
\[\overrightarrow {AD} + \overrightarrow {DC} + \overrightarrow {CC'} = \overrightarrow {AD'} + \overrightarrow {D'C'} \].
Cho hình tứ diện \[ABCD\] có trọng tâm \[G\]. Mệnh đề nào sau đây sai?
\[\overrightarrow {AG} = \frac{2}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right)\].
\[\overrightarrow {AG} = \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right)\].
\[\overrightarrow {OG} = \frac{1}{4}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} } \right)\].
\[\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \].
Trong không gian cho điểm \[O\] và bốn điểm\[A,B,C,D\] không thẳng hàng. Điều kiện cần và đủ để \[A,B,C,D\] tạo thành hình bình hành là
\[\overrightarrow {OA} + \frac{1}{2}\overrightarrow {OB} = \overrightarrow {OC} + \frac{1}{2}\overrightarrow {OD} \].
\[\overrightarrow {OA} + \frac{1}{2}\overrightarrow {OC} = \overrightarrow {OB} + \frac{1}{2}\overrightarrow {OD} \].
\[\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow {OB} + \overrightarrow {OD} \].
\[\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \].
PHẦN 2: CÂU TRẮC NGHIỆM ĐÚNG SAI
Trong không gian cho hình lập phương \(ABCD.A'B'C'D'\) có độ dài cạnh là \(a\). Gọi \(O\)là giao điểm của \(BD\) và \(AC\).
a) Vectơ \[\overrightarrow {A'C} - \overrightarrow {A'A} = \overrightarrow {AB} + \overrightarrow {AD} \]
b) Vectơ \[\overrightarrow {BC'} = \overrightarrow {A'A} + \overrightarrow {B'C'} \].
c) Vectơ \[\overrightarrow {C'O} = \overrightarrow {C'A'} - \overrightarrow {OA'} \]
d) \(\overrightarrow {A'D} .\overrightarrow {A'B} = 0\)
Trong các khẳng định dưới đây khẳng định nào đúng ?
a) Trong không gian lấy ba điểm \(A,B,C\)tùy ý ta luôn có \(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {BC} \).
b) Trong không gian cho hình bình hành \(ABCD\) thì \[\overrightarrow {BA} + \overrightarrow {BC} = \overrightarrow {BD} \] .
c) Với vectơ \(\overrightarrow a \ne \overrightarrow 0 \) và \(k \in \mathbb{R}\) ta luôn có \(\left| {k.\overrightarrow a } \right| = \left| k \right|.\left| {\overrightarrow a } \right|\).
d) Với vectơ \(\overrightarrow a ,\overrightarrow b \) là hai vectơ tùy ý khác vectơ \(\overrightarrow 0 \)ta luôn có \[\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}\].
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Đặt \(\overrightarrow {AB} = \overrightarrow x ;\,\overrightarrow {AD} = \overrightarrow y ;\,\overrightarrow {AA'} = \overrightarrow z \). Xét tính đúng sai của các mệnh đề sau đây:
a) \(\overrightarrow {AC'} = \overrightarrow x + \overrightarrow y + \overrightarrow z \).
b) \(\overrightarrow {A'B} = \overrightarrow x + \overrightarrow z \)
c)Góc giữa véc tơ \(\overrightarrow {BA'} \) và véc tơ \(\overrightarrow {A'C'} \) bằng \({60^\bigcirc }\).
d) Gọi \(M\) là trung điểm của \(BC\). Độ dài véc tơ \(\overrightarrow {A'M} \) bằng \(\frac{{3a}}{2}\).
Cho tứ diện đều\(ABCD\). Gọi \(G\) là trọng tâm của tam giác \(BCD\). Xét tính đúng, sai của các mệnh đề sau đây:
a) \(\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \).
b) \(\overrightarrow {AG} = \frac{1}{3}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} + \frac{2}{3}\overrightarrow {AD} \).
c)\(\overrightarrow {CG} = \frac{1}{3}\overrightarrow {AB} - \frac{2}{3}\overrightarrow {AC} + \frac{1}{3}\overrightarrow {AD} \).
d) Gọi \(I\) là điểm thuộc đoạn \(AG\) và thỏa mãn \(AI = 3IG\). Khi đó \(\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} = \overrightarrow 0 \).
PHẦN 3: CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN
Cho hình hộp \[ABCD.A'B'C'D'\]. Gọi \(M\), \(N\) lần lượt là các điểm trên đoạn \(AC\)và \(C'D\) sao cho, \(DN = \frac{1}{3}DC'\), \(AM = \frac{2}{3}AC\). Khi phân tích \(\overrightarrow {BN} = x.\overrightarrow {BA} + y.\overrightarrow {BC} + z.\overrightarrow {BB'} \) thì giá trị \(x + y + z\) bằng
Cho tứ diện ABCD có \(AB = AC = AD = 1.\) và \[\widehat {BAC} = \widehat {BAD} = 60^\circ ,\,\widehat {CAD} = 90^\circ \]. Gọi \(I\) là điểm trên cạnh \(AB\) sao cho \(AI = 3IB\) và \(J\) là trung điểm của \(CD\). Tính độ dài đoạn thẳng \[IJ\]và làm tròn kết quả đến hàng phần trăm.
Cho hình hộp \[ABCD.A'B'C'D'.\] Gọi \[M\] là điểm trên cạnh \[AC\] sao cho \[AC = 3MC.\] Lấy \[N\] trên đoạn \[C'D\] sao cho \[C'N = x\,C'D.\] Khi \[MN\parallel BD'\] thì giá trị \[x\] (làm tròn kết quả đến hàng phần trăm)
Cho tứ diện đều \(S.ABC\) cạnh \(a\),\(M\) là trung điểm của cạnh \(BC\). Tính \(\cos \left( {\overrightarrow {AM} ,\overrightarrow {SB} } \right)\) (Làm tròn kết quả đến hàng phần trăm).
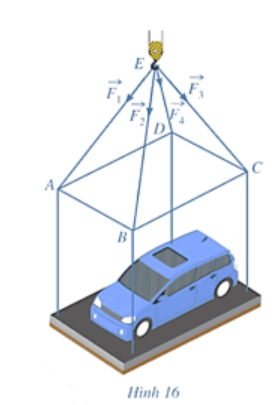
Một chiếc ô tô được đặt trên mặt đáy dưới của một khung sắt dạng hình hộp chữ nhật với đáy trên là hình chữ nhật \(ABCD\), mặt phẳng \(\left( {ABCD} \right)\)song song với mặt phẳng nằm ngang. Khung sắt đó được đặt vào móc \(E\) của chiếc cần cẩu sao cho các đoạn dây cáp \(EA;\,EB;\,EC;\,ED\) bằng nhau và cùng tạo với mặt phẳng \(\left( {ABCD} \right)\)một góc \(\alpha \). Chiếc cần cẩu kéo khung sắt lên theo phương thẳng đứng. Biết các lực căng \(\overrightarrow {{F_1}} ;\,\overrightarrow {{F_2}} ;\,\overrightarrow {{F_3}} ;\,\overrightarrow {{F_4}} \) đều có cường độ là \(4800\,N\), trọng lượng của cả khung sắt chứa xe ô tô là \(7200\sqrt 6 \,N\). Tính \(\sin \alpha \) (làm tròn kết quả đến hàng phần trăm).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật với \(SA = 4,AB = 1,AD = 2\) và \(SA \bot \left( {ABCD} \right)\). Gọi \(M\) là trung điểm của \(AB\). Tính góc giữa hai vectơ \(\overrightarrow {SC} \) và \(\overrightarrow {DM} \).