Đề kiểm tra Khảo sát sự biến thiên và vẽ đồ thị của hàm số (có lời giải) - Đề 5
22 câu hỏi
PHẦN I. CÂU TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN
Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
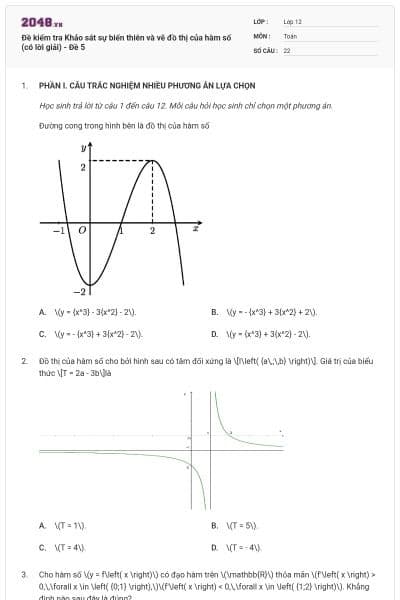
Đường cong trong hình bên là đồ thị của hàm số
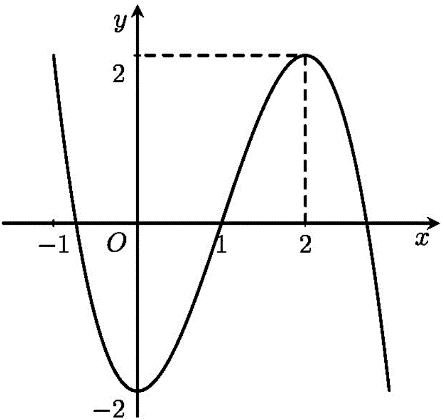
\(y = {x^3} - 3{x^2} - 2\).
\(y = - {x^3} + 3{x^2} + 2\).
\(y = - {x^3} + 3{x^2} - 2\).
\(y = {x^3} + 3{x^2} - 2\).
Đồ thị của hàm số cho bởi hình sau có tâm đối xứng là \[I\left( {a\,;\,b} \right)\]. Giá trị của biểu thức \[T = 2a - 3b\]là![Đồ thị của hàm số cho bởi hình sau có tâm đối xứng là \[I\left( {a\,;\,b} \right)\]. Giá trị của biểu thức \[T = 2a - 3b\] là A. \(T = 1\). B. \(T = 5\). C. \(T = 4\). D.\(T = - 4\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/2-1759205139.png)
\(T = 1\).
\(T = 5\).
\(T = 4\).
\(T = - 4\).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) thỏa mãn \(f'\left( x \right) > 0,\,\forall x \in \left( {0;1} \right),\)\(f'\left( x \right) < 0,\,\forall x \in \left( {1;2} \right)\). Khẳng định nào sau đây là đúng?
Hàm số \(f\left( x \right)\) đồng biến trên các khoảng \(\left( {0;1} \right)\) và \(\left( {1;2} \right)\).
Hàm số \(f\left( x \right)\) đồng biến trên khoảng \(\left( {0;1} \right)\) và nghịch biến trên khoảng \(\left( {1;2} \right)\).
Hàm số \(f\left( x \right)\) nghịch biến trên các khoảng \(\left( {0;1} \right)\) và \(\left( {1;2} \right)\).
Hàm số \(f\left( x \right)\) nghịch biến trên khoảng \(\left( {0;1} \right)\) và đồng biến trên khoảng \(\left( {1;2} \right)\).
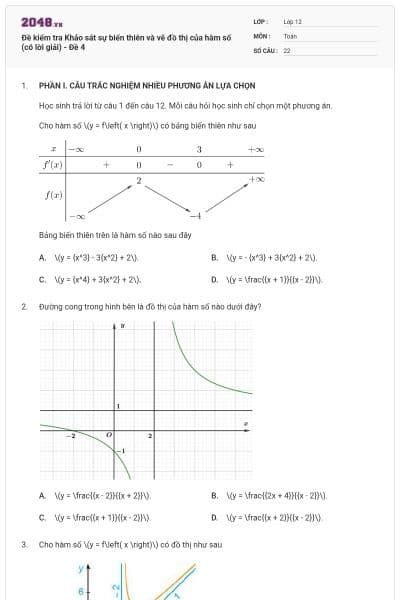
Đường cong trong hình vẽ dưới đây là đồ thị của hàm số \[y = \frac{{{x^2} + 2x - 2}}{{x - 1}}\]. Mệnh đề nào sau đây sai?
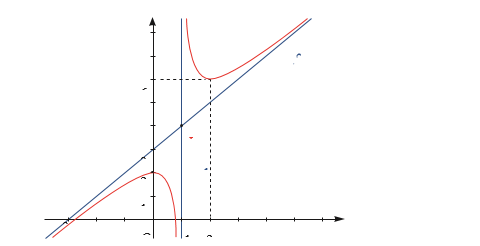
Tâm đối xứng là \[I\left( {1\,;\,3} \right)\].
Tiệm cận đứng là đường thẳng \[x = 1\].
Tiệm cận xiên là đường thẳng \[y = x + 3\].
Đồ thị hàm số đi qua điểm \[A\left( {2\,;\,6} \right)\].
Đồ thị hàm số \(y = {x^3} - 3{x^2} - 2\) cắt trục tung tại điểm có tung độ bằng
\(0\).
\(1\).
\(2\).
\( - 2\).
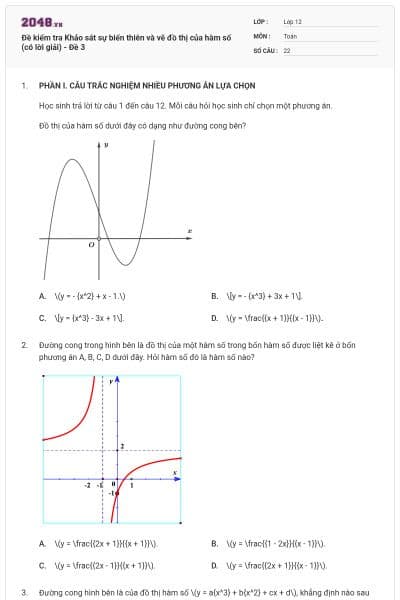
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình dưới. Khẳng định nào sau đây đúng?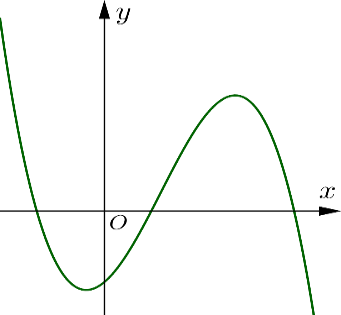
\(a < 0,b < 0,c < 0,d < 0\).
\(a < 0,b > 0,c > 0,d > 0\).
\(a < 0,b > 0,c < 0,d > 0\).
\(a < 0,b > 0,c > 0,d < 0\).
Số giao điểm của đồ thị hàm số \(y = 2x + 4\) và đồ thị hàm số \(y = \frac{{x - 3}}{{x - 1}}\) là
\(0\).
\(1\).
\(3\).
\(2\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:![Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau: Có bao nhiêu giá trị nguyên của \(m\), \(m \in \left( { - 3\,;\,2024} \right]\) để phư (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/4-1759205479.png)
Có bao nhiêu giá trị nguyên của \(m\), \(m \in \left( { - 3\,;\,2024} \right]\) để phương trình \(2f\left( x \right) - m = 0\) có một nghiệm?
\(2019\).
\(2020\).
\(2018\).
\(2021\).
Có bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = \frac{{x + 2}}{{x + 5m}}\) đồng biến trên khoảng \(\left( { - \infty ; - 10} \right)?\)
\(0\).
\(1\).
\(3\).
\(2\).
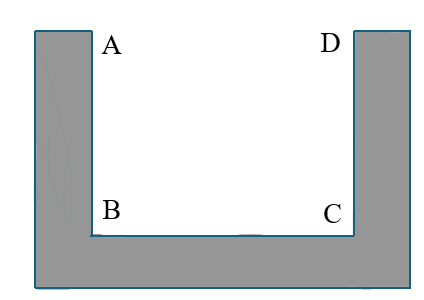
Hình dưới đây là mương dẫn nước thủy lợi tại một địa phương phục vụ tưới tiêu cho ruộng đồng. Phần không gian trong mương để nước chảy có mặt cắt ngang là hình chữ nhật \(ABCD\). Với điều kiện lưu lượng nước qua mương cho phép thì diện tích mặt cắt \(ABCD\) là \(0\,,48\,{m^2}\). Để đảm bảo yêu cầu kỹ thuật tốt nhất cho mương, người ta cần thiết kế sao cho tổng độ dài \(T = AB + \,BC + CD\) là ngắn nhất. Khi đó chiều rộng đáy mương bằng bao nhiêu (biết chiều rộng phải dưới 1m , làm tròn kết quả đến hàng phần trăm).
\(0,78\left( m \right)\).
\(0,97\left( m \right)\).
\(0,98\left( m \right)\).
\(0,83\left( m \right)\).
Có bao nhiêu giátrị nguyên dương của m để hàm số \[y = \frac{{{x^2} + 5x + {m^2} + 6}}{{x + 3}}\] đồng biến trên khoảng \[\left( {1; + \infty } \right)\].
\(4\).
\(5\).
\(9\).
\(3\).
Trong tiết học Toán, giáo viên phát cho \(4\) tổ một tấm bìa hình vuông \(ABCD\) cạnh bằng \(10\,cm\). Giáo viên yêu cầu \(4\) tổ sử dụng tấm bìa này và cắt tấm bìa theo các tam giác cân \(AEB,\,BFC,\,CGD\,,\,DHA\) để sau đó gấp các tam giác \(AEH,\,BEF,\,CFG\,,\,DGH\) sao cho bốn đỉnh \(A\,,\,B\,,\,C\,,\,D\) trùng nhau tạo thành khối chóp tứ giác đều . Khi đó thể tích lớn nhất của khối chóp tứ giác đều tạo thành bằng là
\(\frac{{32\sqrt {10} }}{3}\,\left( {c{m^3}} \right)\).
\(\frac{{16\sqrt {10} }}{3}\,\left( {c{m^3}} \right)\).
\(\frac{{32\sqrt 2 }}{3}\,\left( {c{m^3}} \right)\).
\(\frac{{28\sqrt {10} }}{3}\,\left( {c{m^3}} \right)\).
PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI
Học sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, học sinh chọn đúng hoặc sai.
Cho hàm số \(y = f\left( x \right) = {x^3} - 3{x^2} + 2\) có đồ thị như hình bên dưới
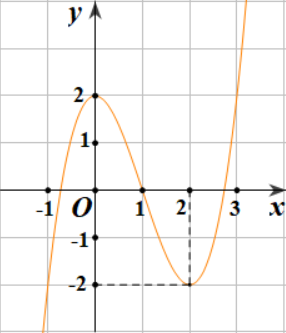
Phát biểu | Đúng | Sai |
a. Hàm số \(f\left( x \right)\) đồng biến trên khoảng \(\left( { - \infty ;2} \right)\). |
|
|
b. Hàm số \(f\left( x \right)\)đạt cực tiểu tại\(x = 2\). |
|
|
c. Đồ thị hàm số\(f\left( x \right)\)có hai điểm cực trị thuộc đường thẳng \(y = - 2x + 2\). |
|
|
| d. Có 1 giá trị nguyên m để phương trình \({x^3} - 3{x^2} + 2 - 2m = 0\)có 3 nghiệm phân biệt. |
|
|
Cho hàm số \[y = \frac{{2x}}{{x + 2}}\] có đồ thị \[\left( C \right)\] và điểm \[M\left( {{x_0};{y_0}} \right) \in \left( C \right)\] \[\left( {{x_0} \ne 0} \right)\]. Xét tính đúng - sai của các phát biểu sau:
a) Tập xác định của hàm số trên là \(\mathbb{R}\).
b) Đồ thị hàm số \[\left( C \right)\] nhận đường thẳng \[y = 2\] là tiệm cận ngang.
c) Hàm số nghịch biến trên \[\left( { - \infty ; - 2} \right)\] và \[\left( { - 2; + \infty } \right)\].
d) Khi khoảng cách từ \[I\left( { - 2;2} \right)\] đến tiếp tuyến của \[\left( C \right)\] tại \[M\] là lớn nhất thì \[2{x_0} + {y_0} = - 4\].
Cho hàm số \(y = f\left( x \right)\)có đồ thị hàm số như hình bên dưới
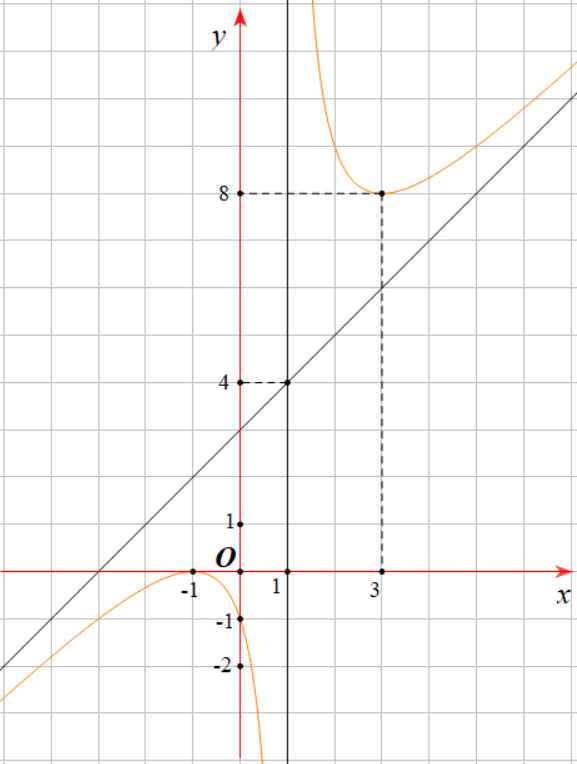
Phát biểu | Đúng | Sai |
a. Hàm số \(f\left( x \right)\) đồng biến trên từng khoảng xác định\(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\). |
|
|
b. Hàm số \(f\left( x \right)\)đạt cực đạitại\(x = - 1\)và đạt cực tiểu tại \(x = 3\). |
|
|
c. Đồ thị hàm số\(f\left( x \right)\)ở hình trên là của hàm số \(y = f\left( x \right) = \frac{{{x^2} + 2x + 1}}{{x - 1}}\) |
|
|
d. Điểm M trên đồ thị hàm số \(f\left( x \right)\) có khoảng cách đến I là nhỏ nhất (với I là giao điểm của hai tiệm cận) với hoành độ dương là\(\sqrt {2\sqrt 2 } + 1\).
|
|
|
Cho hàm số \[y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\] với \[a \ne 0\] có đồ thị như hình vẽ sau
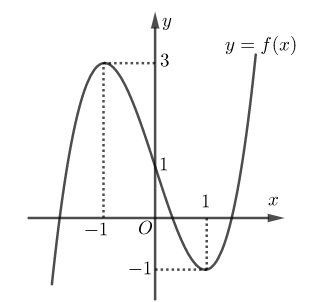
Xét tính đúng - sai của các phát biểu sau:
a) Hàm số đạt cực tiểu tại \(x = - 1\).
b) Phương trình \[f\left( x \right) = 2\] có \[3\] nghiệm phân biệt.
c) Đồ thị trên là đồ thị của hàm số \[y = f\left( x \right) = {x^3} - 3x + 2\].
d) Điểm cực đại của đồ thị hàm số \[y = f\left( {4 - x} \right) + 1\] là \[\left( {5;4} \right)\].
PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN
Học sinh trả lời từ câu 1 đến câu 6
Số giao điểm của đồ thị hàm số \(y = - {x^3} + 6x\) với trục \(Ox\) là
Tìm số điểm cực trị của hàm số \(f\left( x \right) = \frac{{2x + 1}}{{x - 2}}\).
Giá trị lớn nhất của hàm số \[y = \frac{{{x^2} + 4}}{x}\] trên đoạn \[\left[ {1;3} \right]\] bằng bao nhiêu?
Cho hàm số \(y = f\left( x \right)\)có bảng biến thiên như hình dưới. Tìm số nghiệm của phương trình \(f\left( x \right) - 2 = 0.\)
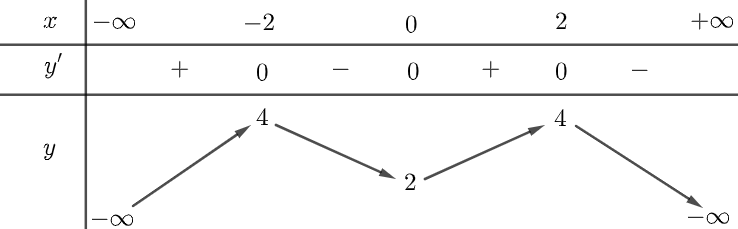
Cho hàm số \(y = f\left( x \right)\)xác định và liên tục trên \(\mathbb{R}\) có bảng biến thiên như sau.
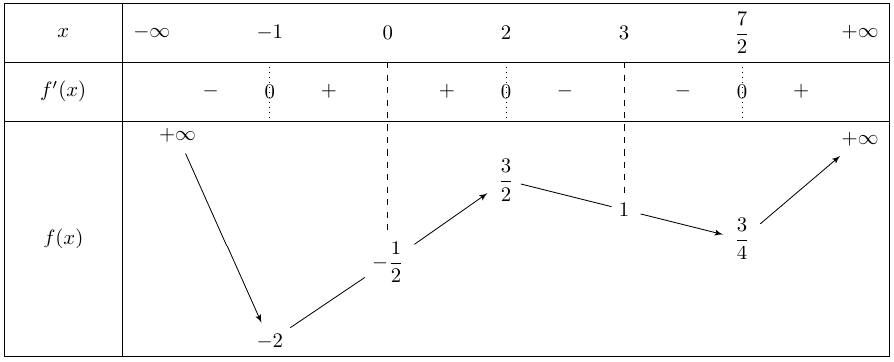
Có bao nhiêu giá trị nguyên của tham số \(m\)để phương trình \(2f\left( {\sqrt {9 - {x^2}} } \right) = m - 2024\) có nghiệm?
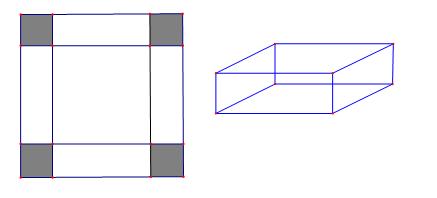
Cho một tấm nhôm hình vuông cạnh \(12\) cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng \(x\) (cm), rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm \(x\) để hộp nhận được có thể tích lớn nhất.