Đề kiểm tra Khảo sát sự biến thiên và vẽ đồ thị của hàm số (có lời giải) - Đề 1
22 câu hỏi
PHẦN I. CÂU TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN
Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
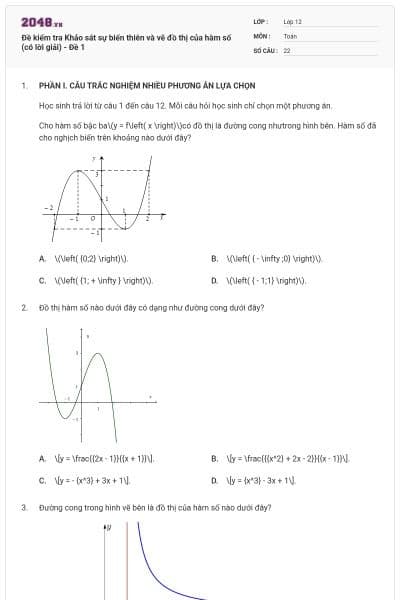
Cho hàm số bậc ba\(y = f\left( x \right)\)có đồ thị là đường cong nhưtrong hình bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
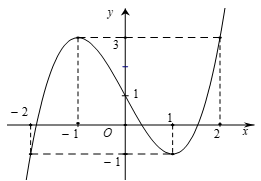
\(\left( {0;2} \right)\).
\(\left( { - \infty ;0} \right)\).
\(\left( {1; + \infty } \right)\).
\(\left( { - 1;1} \right)\).
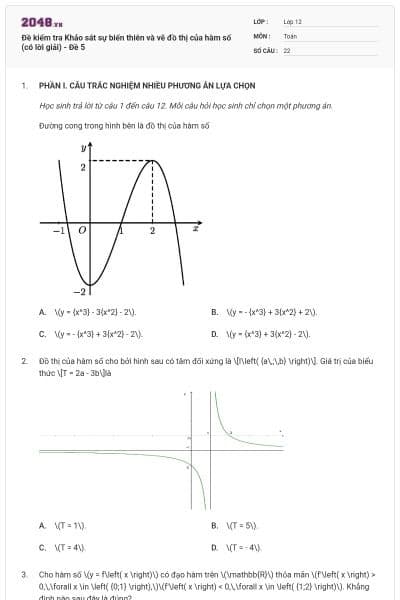
Đồ thị hàm số nào dưới đây có dạng như đường cong dưới đây?
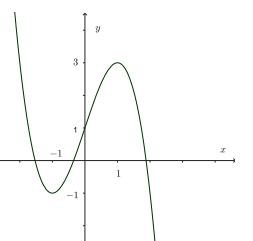
\[y = \frac{{2x - 1}}{{x + 1}}\].
\[y = \frac{{{x^2} + 2x - 2}}{{x - 1}}\].
\[y = - {x^3} + 3x + 1\].
\[y = {x^3} - 3x + 1\].
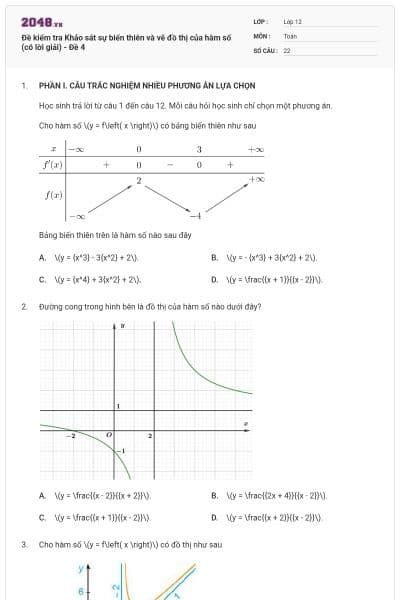
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
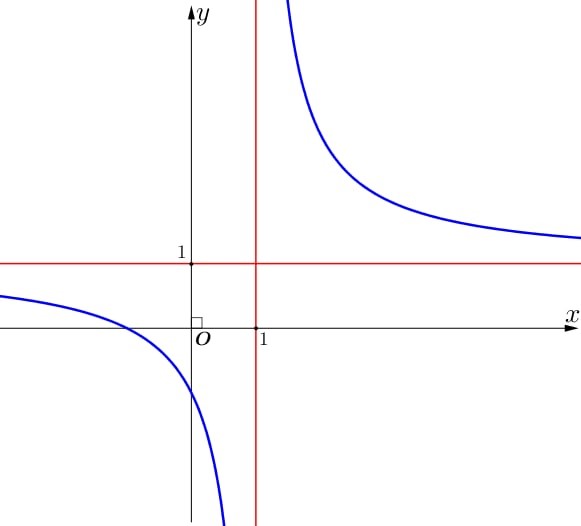
\(y = \frac{{x + 2}}{{x + 1}}\).
\(y = \frac{{x - 1}}{{x + 1}}\).
\(y = \frac{{ - 2x + 1}}{{x - 1}}\).
\(y = \frac{{x + 1}}{{x - 1}}\).
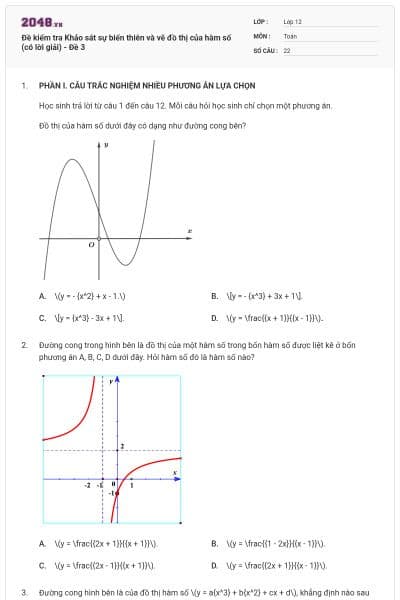
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
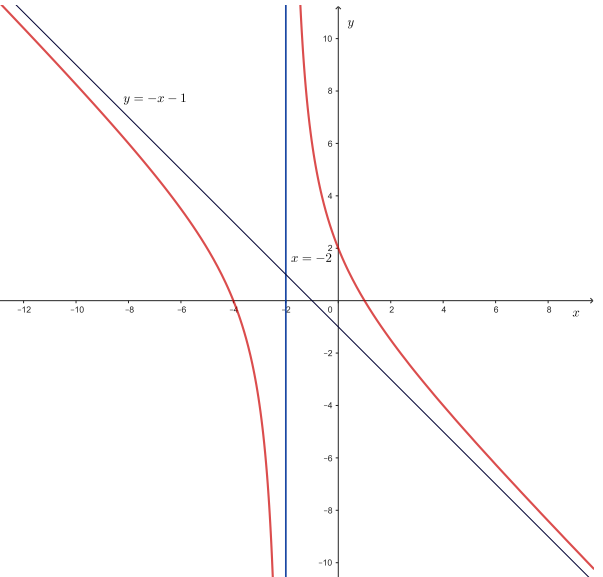
\(y = \frac{{ - {x^2} - 3x + 4}}{{x + 2}}\).
\(y = \frac{{ - {x^2} - 3x + 4}}{{x - 2}}\).
\(y = \frac{{x - 4}}{{x + 2}}\).
\[y = {x^3} - 3x + 1\].
Tiệm cận đứng của đồ thị hàm số \(y = \frac{{2x - 1}}{{x + 3}}\) là đường thẳng nào trong các đường thẳng sau?
\(y = - 3\).
\(y = - 1\).
\(x = - 3\).
\(x = 2\).
Khẳng định nào sau đây đúng về tính đơn điệu của hàm số \[y = \frac{{2x + 4}}{{1 - x}}\]?
Hàm số đồng biến trên các khoảng \[\left( { - \infty ;1} \right)\]và \[\left( {1; + \infty } \right)\].
Hàm số nghịch biến trên các khoảng \[\left( { - \infty ;1} \right)\]\[ \cup \]\[\left( {1; + \infty } \right)\].
Hàm số nghịch biến trên các khoảng \[\left( { - \infty ;1} \right)\]và \[\left( {1; + \infty } \right)\].
Hàm số đồng biến trên các khoảng \[\left( { - \infty ; - 1} \right)\] và \[\left( { - 1; + \infty } \right)\].
Tiệm cận xiên của đồ thị hàm số \[y = f\left( x \right) = \frac{{{x^2} - 3x - 7}}{{x + 2}}\] là
\(y = x + 2\).
\(y = x + 4\).
\(y = x - 3\).
\(y = x - 5\).
Giá trị cực tiểu của hàm số \[y = f\left( x \right) = \frac{{{x^2} + x + 4}}{{x + 1}}\] là
\({y_{CT}} = - 5\).
\({y_{CT}} = 3\).
\({y_{CT}} = 1\).
\({y_{CT}} = - 3\).
Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right) = x\left( {x - 1} \right){\left( {x + 4} \right)^3},\,\forall x \in \mathbb{R}\). Số điểm cực tiểu của hàm số đã cho là
\(2\).
\(3\).
\(4\).
\(1\).
Cho hàm số\[y = \sqrt {2{x^2} + 1} \]. Mệnh đề nào dưới đây đúng?
Hàm số đồng biến trên khoảng \(\left( {0;\, + \infty } \right)\).
Hàm số đồng biến trên khoảng \(\left( { - \infty ;\,0} \right)\).
Hàm số nghịch biến trên khoảng \(\left( {0;\, + \infty } \right)\).
Hàm số nghịch biến trên khoảng \(\left( { - 1;\,1} \right)\).
Từ một tấm bìa hình vuông có độ dài cạnh bằng \(60\,\)cm, người ta cắt bốn hình vuông bằng nhau cạnh \(x\) ở bốn góc rồi gập thành một chiếc hộp có dạng hình hộp chữ nhật không có nắp (hình minh họa). Cạnh hình vuông bị cắt có giá trị bao nhiêu thì thể tích của chiếc hộp là lớn nhất?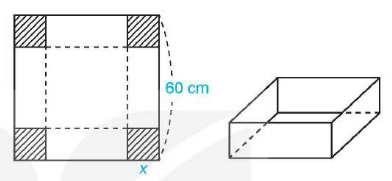
\(x = 10\)cm.
\(x = 12\)cm.
\(x = 15\)cm.
\(x = 20\)cm.
Trong một nhà hàng, mỗi tuần để chế biến \(x\) phần ăn (\(x\) lấy giá trị trong khoảng từ \(30\) đến \(120\)) thì chi phí trung bình (đơn vị nghìn đồng) của một phần ăn được cho bởi công thức: \(\overline C \left( x \right) = 2x - 230 + \frac{{7200}}{x}\). Số phần ăn \(x\) là bao nhiêu thì chi phí trung bình của mỗi phần ăn là thấp nhất?
\(x = 40\).
\(x = 50\).
\(x = 60\).
\(x = 70\).
PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI
Học sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, học sinh chọn đúng hoặc sai.
Cho hàm số \[y = \frac{1}{3}{x^3} - 2{x^2} + mx + 1\].
a) Hàm số đồng biến trên \[\mathbb{R}\] khi \[m = 5\].
b) Hàm số có cực trị khi \[m = 5\].
c) Để hàm số có \[2\] cực trị thì \[m < 4\].
d) Khi \[m \ge 4\]thì hàm số đồng biến trên \[\left( {1,4} \right)\].
Cho hàm số \[y = \frac{{x + 1}}{{x - 3}}\].
a) Hàm số đồng biến trên \[( - \infty ;3)\].
b) Hàm số có tiệm cận ngang \[y = 1\].
c) Tỉ số giữa GTLN và GTNN của hàm số \[y = \frac{{x + 1}}{{x - 3}}\] trên \[{\rm{[4}};7]\]là \[\frac{5}{4}\].
d) Đường thẳng \[y = x - m\] cắt \[y = \frac{{x + 1}}{{x - 3}}\] tại \[2\]điểm phân biệt \[\forall m \in \mathbb{R}\].
Cho hàm số \(y = \frac{{a{x^2} + bx + c}}{{mx + n}}\) có đồ thị như hình vẽ bên dưới.
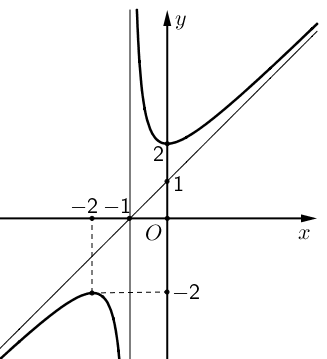
a) Hàm số đã cho nghịch biến trên khoảng \(\left( { - 2;0} \right)\).
b) Đồ thị của hàm số đã cho có tiệm cận đứng \(x = - 1\).
c) Đồ thị của hàm số đã cho có tiệm cận xiên \(y = x + 1\).
d) Gọi \(A,B\) là 2 điểm cực trị của hàm số đã cho, diện tích tam giác \(OAB\) bằng \(\sqrt 5 \).
Cho hàm số \(y = \frac{{{x^2} + x - 3}}{{x + 2}}\) có đồ thị \(\left( C \right)\).
a) Hàm số luôn đồng biến trên các khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( { - 2; + \infty } \right)\).
b) Đồ thị \(\left( C \right)\) của hàm số đã cho có tiệm cận đứng \(x = - 2\).
c) Đồ thị \(\left( C \right)\) của hàm số đã cho có tiệm cận xiên \(y = x - 3\).
d) Gọi \(S\) là tập hợp tất cả các điểm có tọa độ nguyên thuộc đồ thị \(\left( C \right)\). Khi đó, số phần tử của \(S\) là \(3\).
PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN
Học sinh trả lời từ câu 1 đến câu 6.
Khoảng cách từ điểm cực tiểu của đồ thị hàm số \(y = {x^3} - 2{x^2} + x - 1\) đến trục hoành là
Cho hàm số \(y = \frac{{ax + 2}}{{cx + b}}\) có đồ thị như hình vẽ sau. Tính giá trị của biểu thức \(S = a + b + c\).
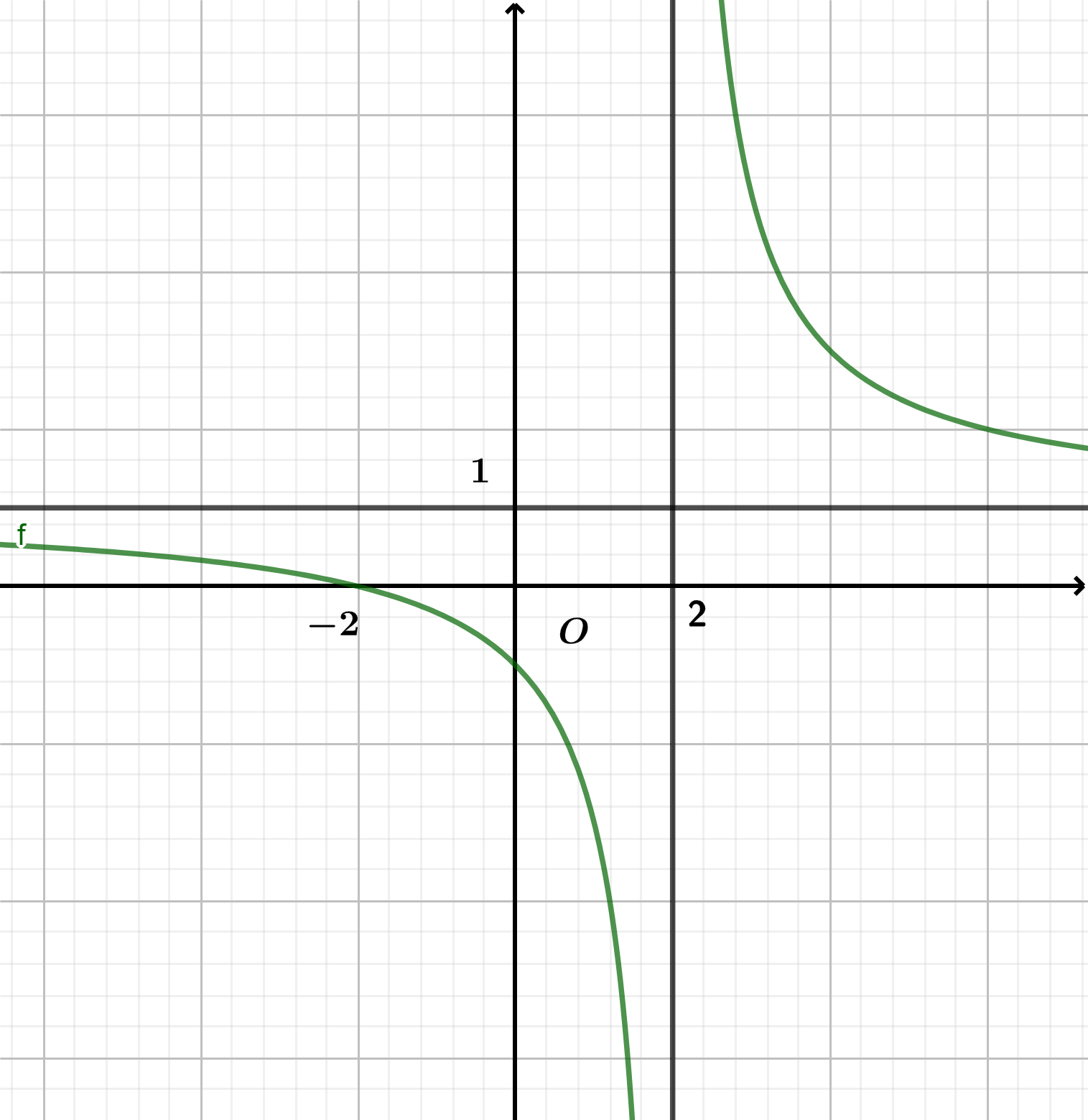
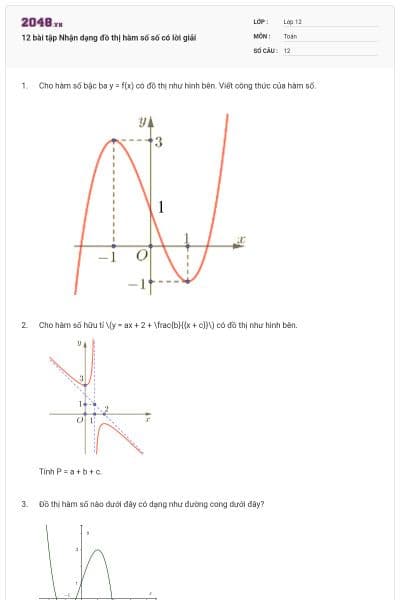
Cho hàm số hữu tỉ \[y = ax + 2 + \frac{b}{{x + c}}\] có đồ thị như hình bên dưới. Tính\(P = a + b + c.\)
![Cho hàm số hữu tỉ \[y = ax + 2 + \frac{b}{{x + c}}\] có đồ thị như hình bên dưới. Tính\(P = a + b + c.\) (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/12-1759200440.png)
Giả sử chi phí cho xuất bản \(x\) cuốn tạp chí (gồm: lương cán bộ, công nhân viên, giấy in,...) được cho bởi công thức:
\(C(x) = 0,0001{x^2} - 0,2x + 10000,\)
trong đó \(C(x)\) được tính theo đơn vị là vạn đồng (1 vạn đồng \( = \) 10000 đồng). Chi phí phát hành cho mỗi cuốn là 4 nghìn đồng. Tỉ số \(M(x) = \frac{{T(x)}}{x}\) được gọi là chi phí trung bình cho một cuốn tạp chí khi xuất bản \(x\) cuốn và tổng chi phí \(T(x)\) (xuất bản và phát hành) cho \(x\) cuốn tạp chí. Tìm chi phí trung bình thấp nhất cho một cuốn tạp chí là bao nhiêu vạn đồng, biết rằng nhu cầu hiện tại xuất bản không quá 30000 cuốn?
Một thành phố nằm trên một con sông chảy qua hẻm núi. Hẻm có chiều ngang 80m, một bên cao \[40{\rm{ m}}\] và một bên cao \[30{\rm{ m}}\]. Một cây cầu sẽ được xây dựng bắc qua sông và hẻm núi. Sơ đồ thiết kế của cây cầu được gắn hệ trục tọa độ như hình vẽ dưới đây.
![Hai cột đỡ dọc \[MN\] và \[PQ\] ( song song với trục \[Oy\]) là đoạn nối giữa khung của Parabol và đường \[XY\]. Tính tổng độ d (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/14-1759200516.png)
Con đường \[XY\] xuyên qua hẻm núi được mô hình hóa bằng phương trình: \[y = \frac{{{x^3}}}{{25600}} - \frac{{3x}}{{16}} + 35\].
Hai cột đỡ dọc \[MN\] và \[PQ\] ( song song với trục \[Oy\]) là đoạn nối giữa khung của Parabol và đường \[XY\]. Tính tổng độ dài đoạn \[MN\]và \[PQ\] biết rằng \[N\]và \[Q\] là hai điểm đối xứng qua \[Oy\]; \[MN\] là đoạn có độ dài lớn nhất ( làm tròn kết quả đến hàng phần chục).
Ông Vinh đang ở trong rừng để đào vàng. Anh ta tìm thấy vàng ở \[{\rm{X}}\], cách điểm \[A\]: \[3{\rm{ km}}\]. Điểm \[A\] nằm trên đường bờ biển ( đường bờ biển là đường thẳng). Trại của Ông Vinh nằm ở \[Y\], cách điểm \[B\]: \[3{\rm{ km}}{\rm{.}}\] Điểm \[B\] cũng thuộc đường bờ biển. Biết rằng \[AB = 3{\rm{ km, }}AM = NB = x{\rm{ km}}\]và \[AX = BY = 3{\rm{ km}}{\rm{.}}\] (Như hình vẽ sau)
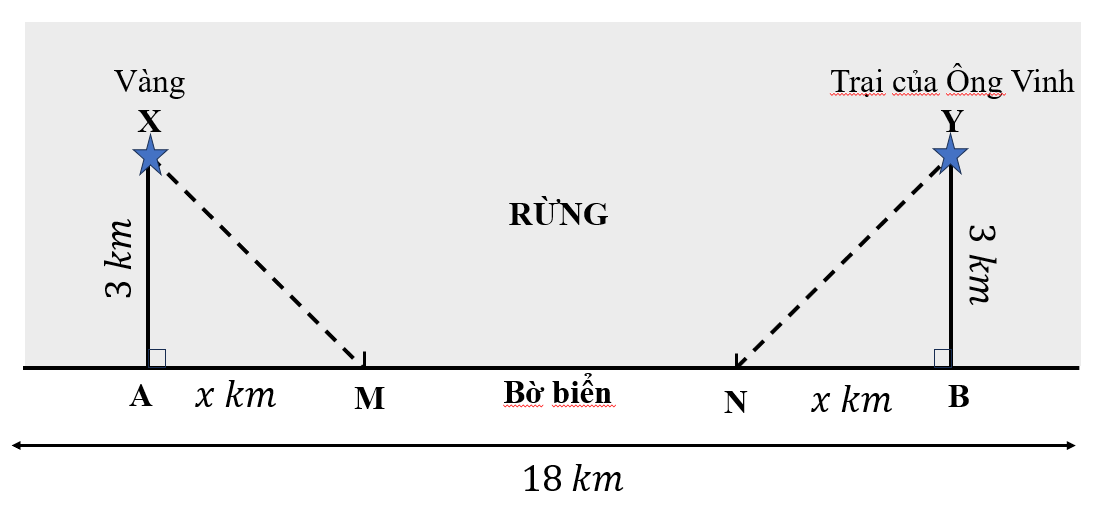
Khi đang đào vàng, Ông Vinh bị rắn cắn, chất độc lan vào máu. Sau khi bị cắn, nồng độ chất độc trong máu tăng theo thời gian được tính theo phương trình
\[y = 50\log \left( {t + 2} \right)\]
Trong đó, \[y\]là nồng độ, \[t\] là thời gian tính bằng giờ sau khi bị rắn cắn.
Ông Vinh cần quay trở lại trại để lấy thuốc giải độc. Ông ấy chạy trong rừng và trên bãi biển với vận tốc lần lượt là \[5{\rm{ km/h}}\]và \[13{\rm{ km/h}}{\rm{.}}\]
Để về đến trại Ông Vinh cần chạy từ trong rừng qua điểm M, N trên bãi biển.
Tính nồng độ chất độc trong máu thấp nhất khi ông Vinh về đến trại ( làm tròn đáp án đến hàng phần chục).