Đề kiểm tra Khảo sát sự biến thiên và vẽ đồ thị của hàm số (có lời giải) - Đề 2
22 câu hỏi
PHẦN I. CÂU TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN
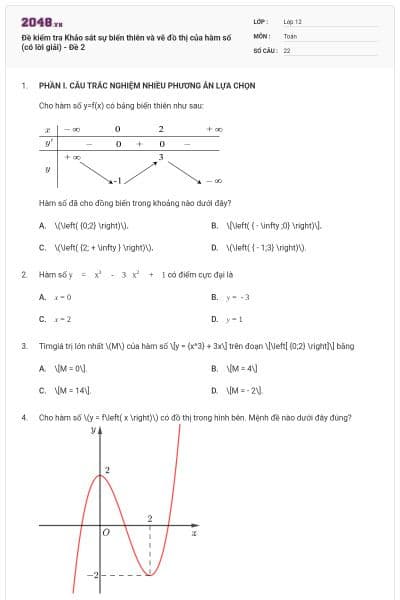
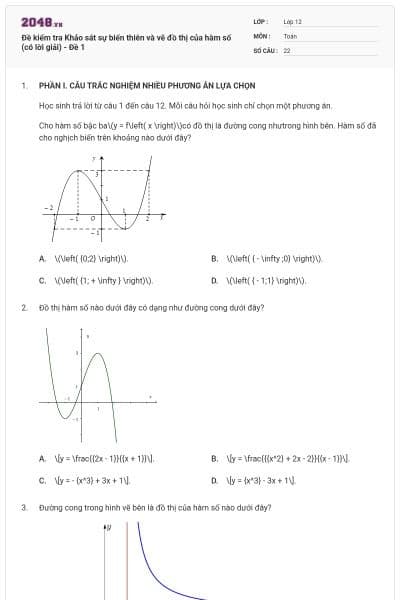
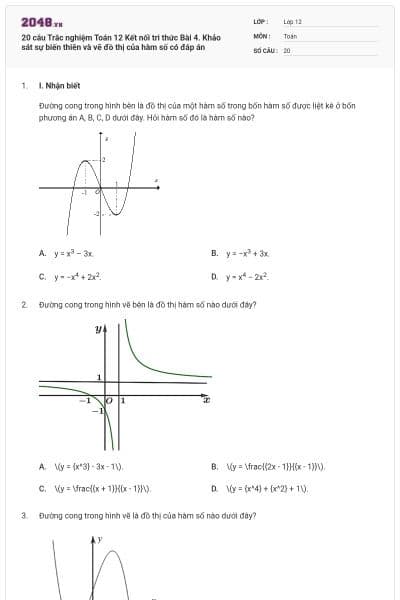
Cho hàm số y=f(x) có bảng biến thiên như sau:
Hàm số đã cho đồng biến trong khoảng nào dưới đây?
\(\left( {0;2} \right)\).
\[\left( { - \infty ;0} \right)\].
\(\left( {2; + \infty } \right)\).
\(\left( { - 1;3} \right)\).
Hàm số có điểm cực đại là
Tìmgiá trị lớn nhất \(M\) của hàm số \[y = {x^3} + 3x\] trên đoạn \[\left[ {0;2} \right]\] bằng
\[M = 0\].
\[M = 4\]
\[M = 14\].
\[M = - 2\].
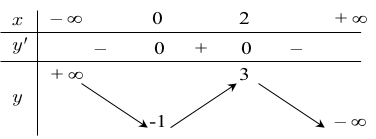
Cho hàm số \(y = f\left( x \right)\) có đồ thị trong hình bên. Mệnh đề nào dưới đây đúng?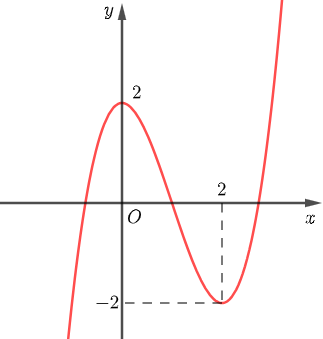
Hàm số có giá trị cực tiểu bằng \(2\).
Hàm số có ba điểm cực trị.
Hàm số có giá trị cực đại bằng \(0\).
Hàm số đạt cực đại tại \(x = 0\).
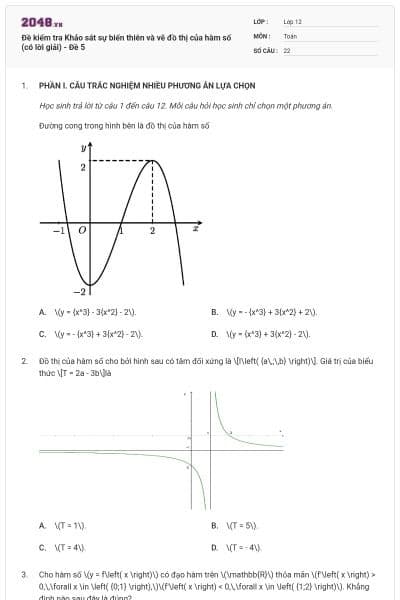
Đường cong ở hình bên dưới là đồ thị của hàm số \(y = \frac{{ax + b}}{{cx + d}}\)với \[a\],\[b\],\[c\],\[d\] là các số thực.
Mệnh đề nào dưới đây đúng?
\(y' > 0\),\(\forall x \ne 2\).
\(y' > 0\),\(\forall x \ne 3\).
\(y' < 0\),\(\forall x \ne 2\).
\(y' < 0\),\(\forall x \ne 3\).
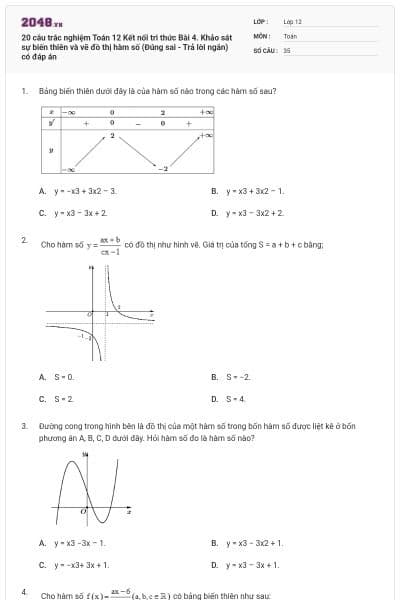
Bảng biến thiên trong hình dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
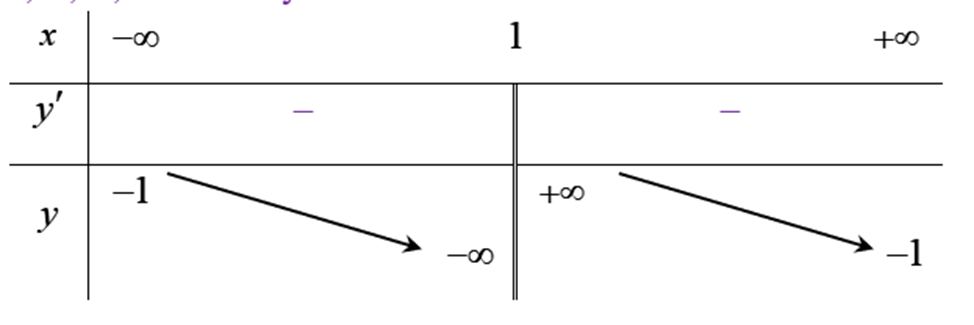
\(y = \frac{{x + 3}}{{x - 1}}\).
\(y = \frac{{ - x - 2}}{{x - 1}}\).
\(y = \frac{{ - x + 3}}{{x - 1}}\).
\(y = \frac{{ - x - 3}}{{x - 1}}\).
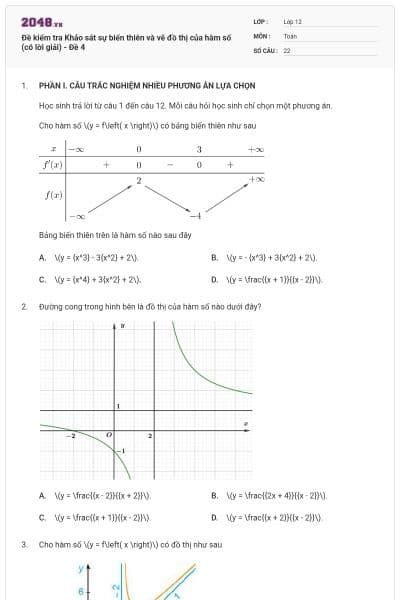
Bảng biến thiên sau là của hàm số nào dưới đây?
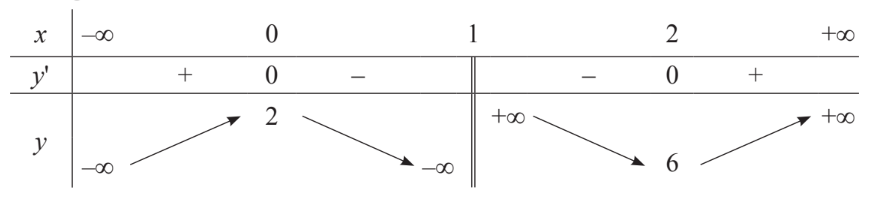
\(y = \frac{{{x^2} + 2x - 2}}{{x - 1}}\).
\(y = \frac{{{x^2} + 2x - 2}}{{x + 1}}\).
\(y = \frac{{{x^2} + 2x + 2}}{{x - 1}}\).
\(y = \frac{{{x^2} + 2x + 2}}{{x + 1}}\).
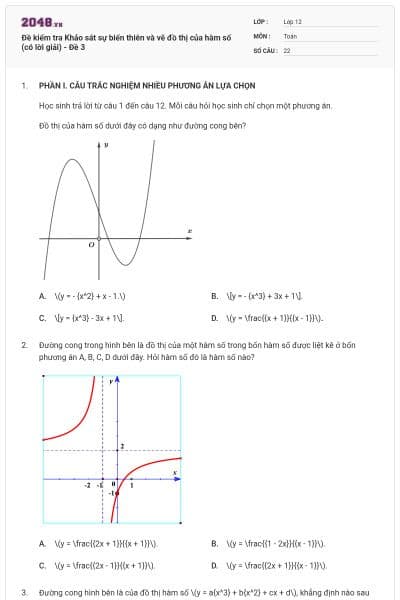
Đường cong ở hình dưới đây là đồ thị của hàm số
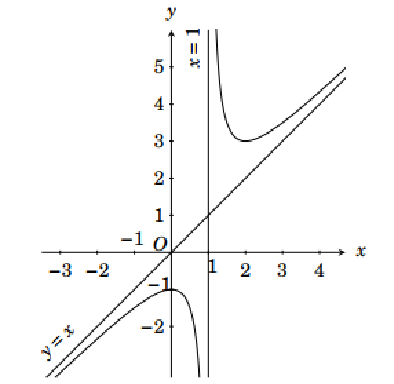
\(y = \frac{{{x^2} + x - 1}}{{x - 1}}\).
\(y = \frac{{{x^2} - x + 1}}{{x - 1}}\).
\(y = \frac{{{x^2} - 4x - 1}}{{x + 1}}\).
\[y = \frac{{{x^2} - 4x + 5}}{{x - 2}}\].
Giá trị cực tiểu của hàm số \(y = {x^2}\ln x\) là
\(\frac{1}{e}\).
\( - \frac{1}{e}\).
\( - \frac{1}{{2e}}\).
\(\frac{1}{{2e}}\).
Cho hàm số \(y = \sqrt {2x - {x^2}} \). Khẳng định nào sau đây đúng?
Hàm số đồng biến trên khoảng \(\left( { - 1;0} \right)\).
Hàm số đồng biến trên khoảng \(\left( {1;2} \right)\).
Hàm số đồng biến trên khoảng \(\left( {0;1} \right)\).
Hàm số nghịch biến trên khoảng \(\left( {0;1} \right)\).
Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong \(t\) giờ được cho bởi công thức \[c\left( t \right) = \frac{t}{{{t^2} + 1}}\]\(\left( {{\rm{mg}}/L} \right)\). Sau khi tiêm thuốc bao lâu thì nồng độ thuốc trong máu của bệnh nhân cao nhất?
4 giờ.
1 giờ.
3 giờ.
2 giờ.
Một mảnh vườn hình chữ nhật có diện tích bằng \(150\,{{\rm{m}}^{\rm{2}}}\). Biết độ dài một cạnh của mảnh vườn là \(x - 2\,\left( {\rm{m}} \right)\). Biểu thức tính chu vi của mảnh vườn là \(P\left( x \right)\) (mét). Phương trình đường tiệm cận xiên của đồ thị hàm số \(P\left( x \right)\) là:
\(y = 2x - 4\).
\(y = 2x\).
\(y = 2x + 4\).
\(y = x - 2\).
PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI
Học sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, học sinh chọn đúng hoặc sai.
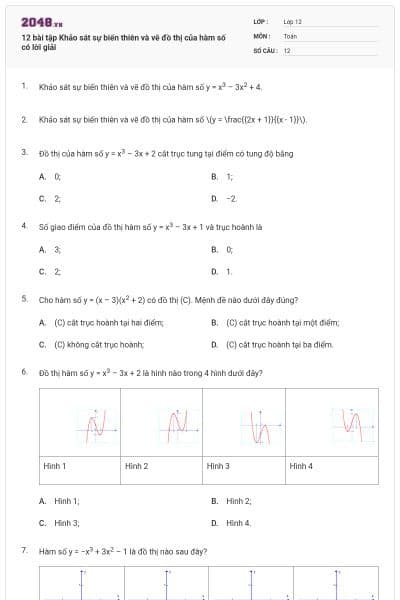
Cho hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d,\,\,\,\left( {a \ne 0} \right)\) có đồ thị trong hình dưới đây.
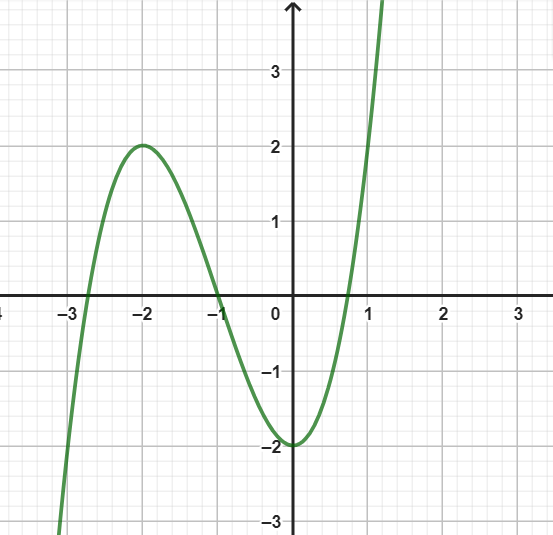
Xét tính đúng, sai của các mệnh đề sau
a) Hệ số \(a > 0\).
b) Hàm số đạt cực đại tại \(x = 0\).
c) Phương trình \(3f\left( x \right) - 5 = 0\) có 3 nghiệm phân biệt.
d) \(f\left( x \right) = {x^3} - 3{x^2} - 2\).
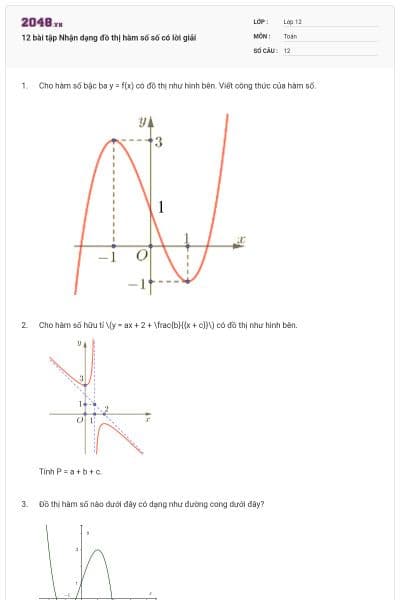
Cho hàm số \(f\left( x \right) = \frac{{ax + 3}}{{bx + c}}\) \(\left( {a,b,c \in \mathbb{R}} \right)\) có bảng biến thiên như sau:
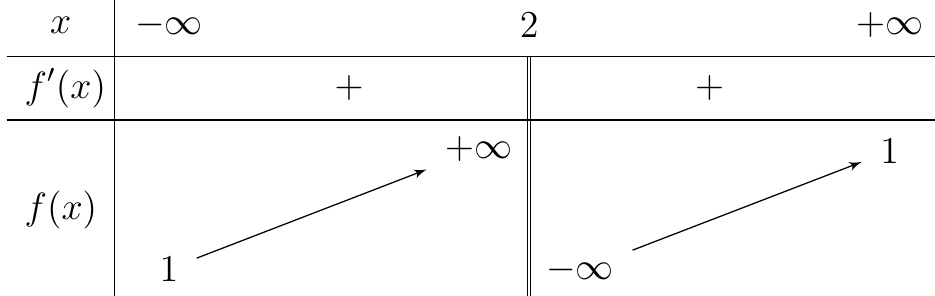
Xét tính đúng, sai của các mệnh đề sau
a) Đồ thị hàm số có đường tiệm cận đứng là \(x = 2\).
b) Đồ thị hàm số có đường tiệm cận ngang là \(y = 2\).
c) \(f\left( { - 5} \right) < 0\).
d) Trong các số \(a,b\) và \(c\) chỉ có một số âm.
Cho hàm số \(y = f\left( x \right) = \frac{{{x^2} + 3x + 1}}{{x + 1}}\) có đồ thị \(\left( C \right)\). Khi đó
a) Tập xác định của hàm số \(f\left( x \right)\) là \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\).
b) Hàm số \(f\left( x \right)\) nghịch biến trên từng khoảng xác định của nó.
c) Đường thẳng \(y = x + 2\) là đường tiệm cận xiên của \(\left( C \right)\).
d) Số điểm trên \(\left( C \right)\) có tọa độ nguyên là \(3\).
Anh B chế tạo một bể cá có dạng khối hình hộp chữ nhật không nắp có thể tích \(0,096\,{{\rm{m}}^3}\), chiều cao \(h = 0,6\,{\rm{m}}\), chiều rộng \(x\), chiều dài \(y\), với \(x > 0,\,y > 0\). Anh B dùng loại kính để làm các mặt bên có giá \(70.000\) đồng/\({{\rm{m}}^2}\) và loại kính để làm mặt đáy có giá \(100.000\) đồng/\({{\rm{m}}^2}\). Mọi chi phí khác xem như không đáng kể. Khi đó
a) Hàm số biểu thị \(y\) theo \(x\) là \(y = \frac{{0,16}}{x}\).
b) Chi phí mua kính để làm đáy bể là \(11200\) đồng.
c) Biểu thức tính chi phí làm các mặt xung quanh là \({C_{{\rm{xq}}}} = 84000.\left( {x + \frac{{0,16}}{x}} \right)\).
d) Chi phí làm bể cá thấp nhất là \(100000\) đồng.
PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN
Học sinh trả lời từ câu 1 đến câu 6.
Cho hàm số \(y = - {x^3} - m{x^2} + \left( {4m + 9} \right)x + 5\), với \(m\) là tham số. Có bao nhiêu giá trị nguyên của \(m\) để hàm số nghịch biến trên \(\left( { - \infty ; + \infty } \right)\).
Có bao nhiêu giá trị nguyên \(m\) thuộc đoạn \(\left[ { - 5;5} \right]\), để đường thẳng \(d:y = mx + 1\) cắt đồ thị hàm số \(\left( C \right):y = \frac{{ - 2x + 1}}{{x - 1}}\) tại hai điểm phân biệt?
Gọi \[m\] là giá trị nhỏ nhất của hàm số \[y = \frac{{{x^2} - 2x + 5}}{{x - 1}}\] trên khoảng \[\left( {1;\infty } \right)\]. Giá trị của \[m\] bằng bao nhiêu?
Một công ty chuyên sản xuất dụng cụ thể thao nhận được đơn đặt hàng sản xuất \(8000\) quả bóng rổ. Công ty có một số máy móc, mỗi máy có khả năng sản xuất \(30\) bóng rổ trong một giờ. Chi phí thiết lập mỗi máy là\(200\) nghìn đồng. Sau khi thiết lập, quá trình sản xuất sẽ diễn ra hoàn toàn tự động và chỉ cần có người giám sát. Chi phí trả cho người giám sát là \(192\) nghìn đồng mỗi giờ. Công ty cần sử dụng bao nhiêu máy móc để chi phí hoạt động đạt mức thấp nhất?
Một vật chuyển động theo quy luật \[s\left( t \right) = {t^3} - 3{t^2} - 9t + 2\]. Hỏi tại thời điểm nào thì vận tốc của vật đạt giá trị nhỏ nhất?
Trong phòng thí nghiệm người ta xác định được số lượng vi khuẩn được nuôi cấy tính theo công thức \[N\left( t \right) = 1000 + \frac{{100t}}{{100 + {t^2}}}\] (con vi khuẩn). Tính số lượng vi khuẩn lớn nhất kể từ khi nuôi cấy.