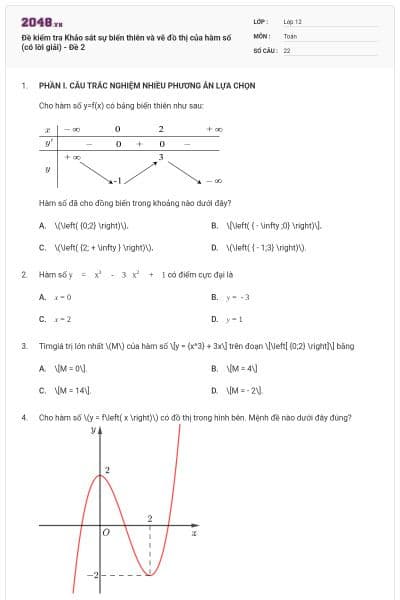
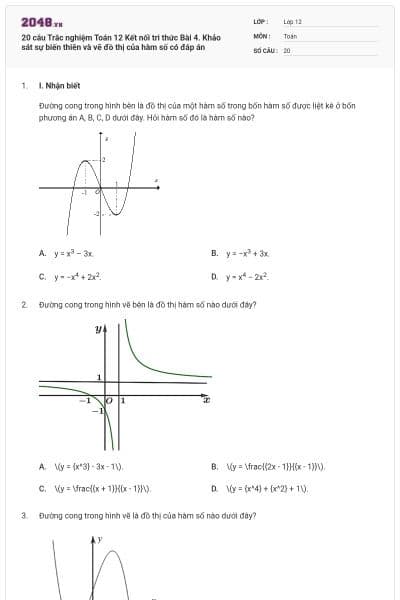
12 bài tập Khảo sát sự biến thiên và vẽ đồ thị của hàm số có lời giải
12 câu hỏi
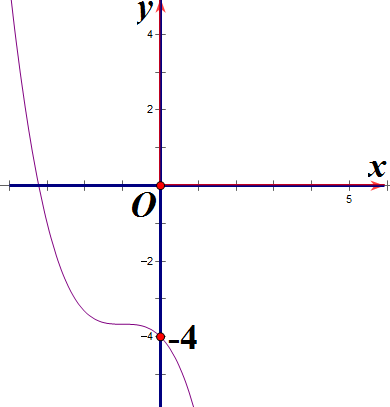
Khảo sát sự biến thiên và vẽ đồ thị của hàm số y = x3 – 3x2 + 4.
Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = \frac{{2x + 1}}{{x - 1}}\).
Đồ thị của hàm số y = x3 – 3x + 2 cắt trục tung tại điểm có tung độ bằng
0;
1;
2;
−2.
Số giao điểm của đồ thị hàm số y = x3 – 3x + 1 và trục hoành là
3;
0;
2;
1.
Cho hàm số y = (x – 3)(x2 + 2) có đồ thị (C). Mệnh đề nào dưới đây đúng?
(C) cắt trục hoành tại hai điểm;
(C) cắt trục hoành tại một điểm;
(C) không cắt trục hoành;
(C) cắt trục hoành tại ba điểm.
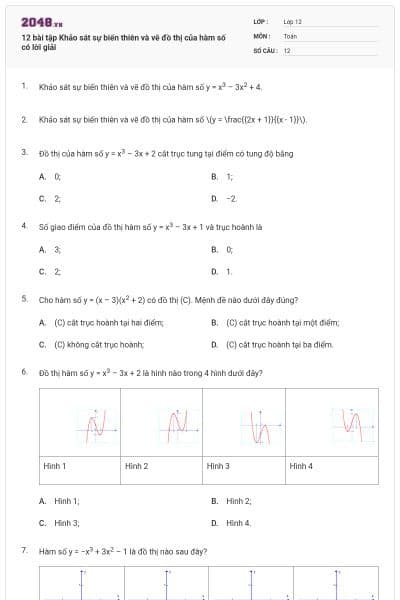
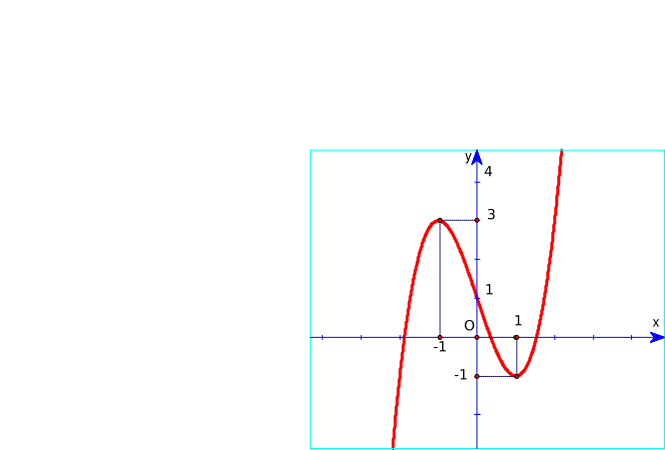
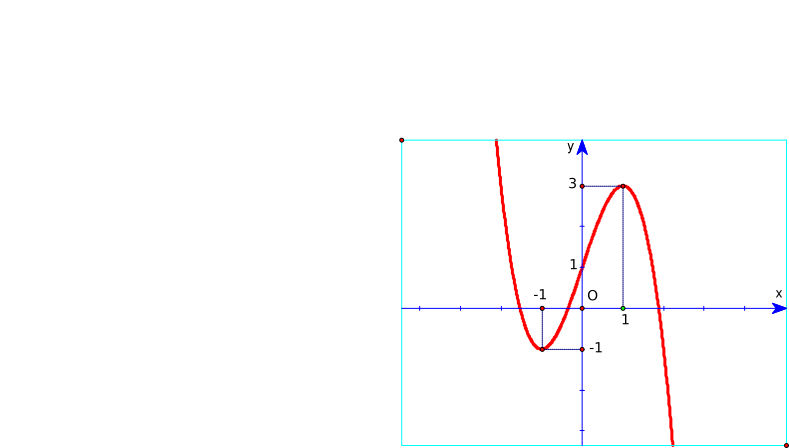
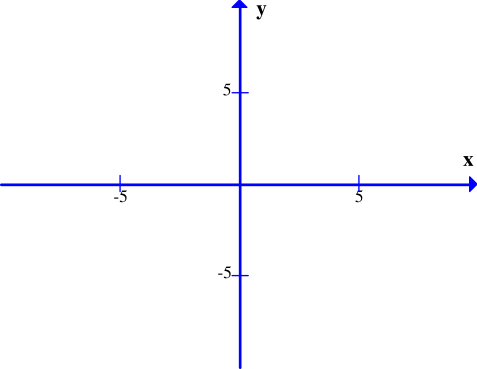
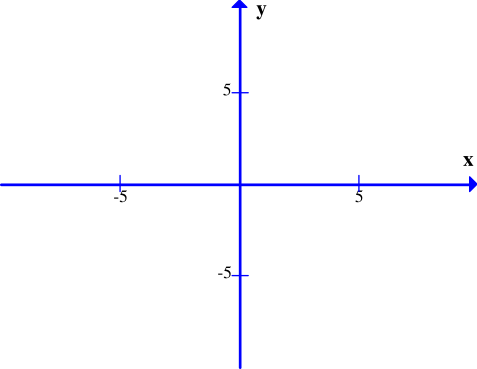
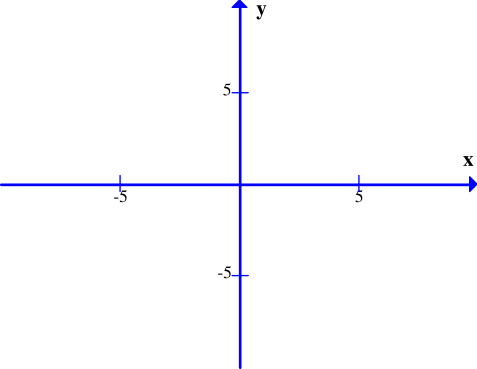
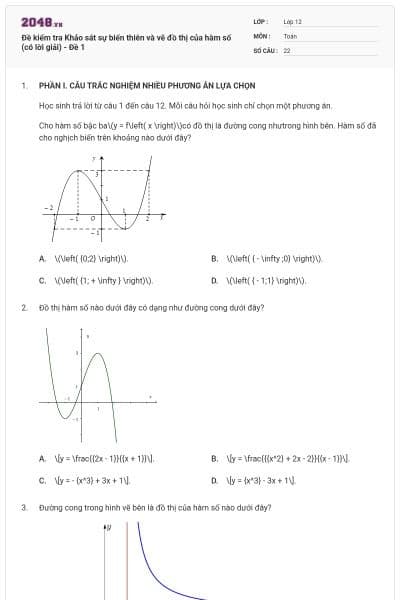
Đồ thị hàm số y = x3 – 3x + 2 là hình nào trong 4 hình dưới đây?
|
|
|
|
Hình 1 | Hình 2 | Hình 3 | Hình 4 |
Hình 1;
Hình 2;
Hình 3;
Hình 4.
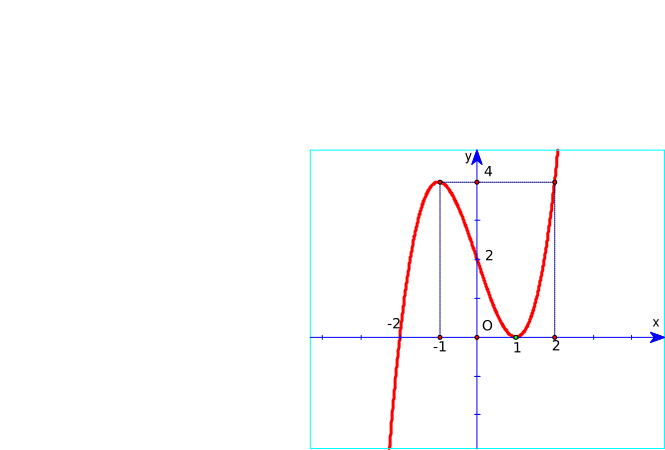
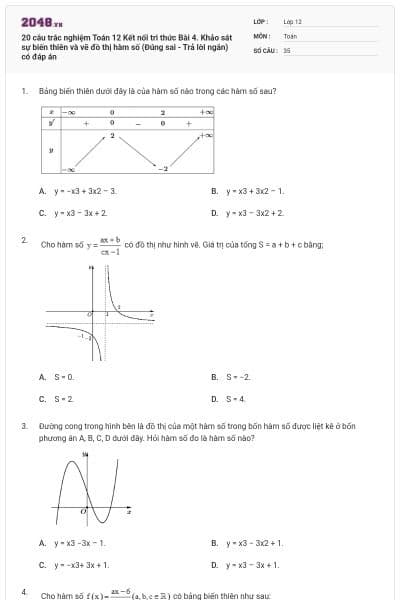
Hàm số y = −x3 + 3x2 – 1 là đồ thị nào sau đây?
|
|
|
|
Hình 1 | Hình 2 | Hình 3 | Hình 4 |
Hình 1;
Hình 2;
Hình 3;
Hình 4.
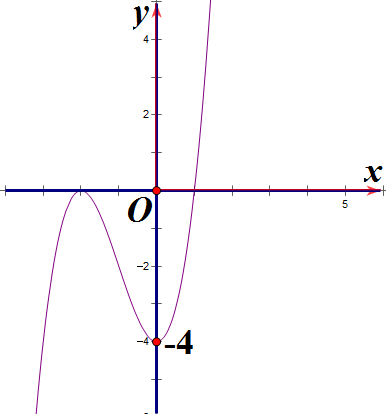
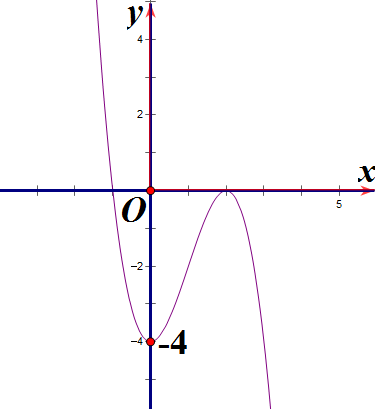
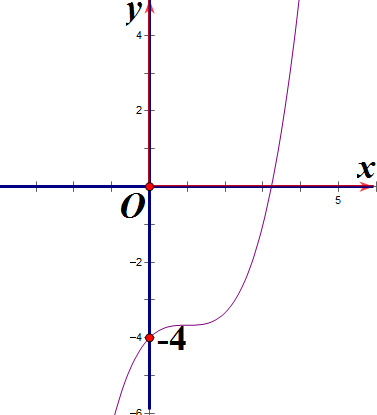
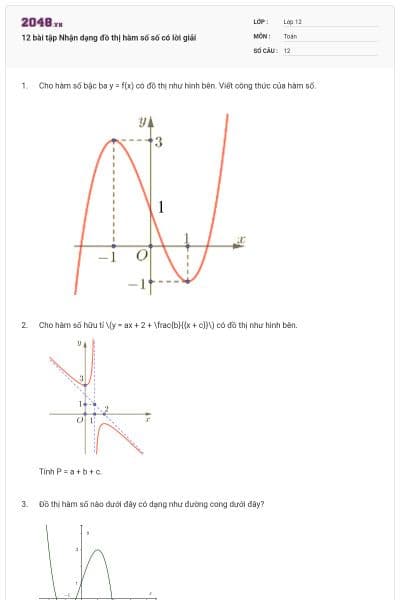
Hàm số y = x3 + 3x2 – 4 có đồ thị là hình nào sau đây?
|
|
|
|
Hình 1 | Hình 2 | Hình 3 | Hình 4 |
Hình 1;
Hình 2;
Hình 3;
Hình 4.
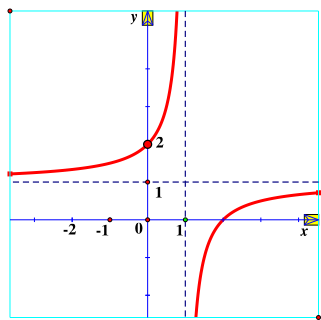
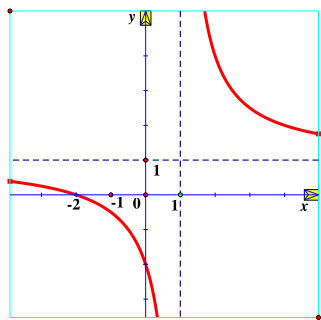
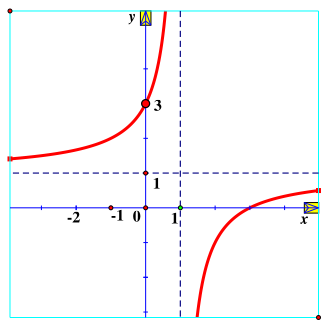
Hàm số \(y = \frac{{x - 2}}{{x - 1}}\) có đồ thị là hình vẽ nào sau đây?
|
|
|
|
|
| Hình 1 | Hình 2 | Hình 3 | Hình 4 |
Hình 1;
Hình 2;
Hình 3;
Hình 4.
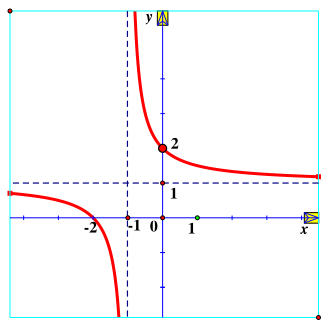
Cho hàm số \(y = f\left( x \right) = \frac{{{x^2} + 3x + 1}}{{x + 1}}\) có đồ thị (C). Chọn đáp án đúng.
Tập xác định của hàm số f(x) là D = ℝ\{−1};
Hàm số f(x) nghịch biến trên từng khoảng xác định của nó;
Đường thẳng y = x + 3 là đường tiệm cận xiên của (C);
Điểm I(−1; −1) là tâm đối xứng của đồ thị hàm số.
Cho hàm số \[y = \frac{{{x^2} + 2x - 2}}{{x - 1}}\]. Mệnh đề nào sau đây sai?
Tâm đối xứng là I(1; 3);
Tiệm cận đứng là đường thẳng x = 1;
Tiệm cận xiên là đường thẳng y = x + 3;
Đồ thị hàm số đi qua điểm A(2; 6).
Cho hàm số \(y = \frac{{2x + 3}}{{x - 1}}\) có đồ thị (C). Chọn đáp án đúng.
Đồ thị hàm số (C) nhận đường thẳng x = 2 là tiệm cận ngang;
Đồ thị hàm số (C) nhận I(2; 3) là tâm đối xứng;
Tiếp tuyến của (C) tại giao điểm của (C) với Oy có phương trình y = −5x – 3;
Tích khoảng cách từ một điểm bất kỳ trên (C) tới 2 đường tiệm cận của nó luôn bằng 3.