20 câu Trắc nghiệm Toán 12 Kết nối tri thức Bài 4. Khảo sát sự biến thiên và vẽ đồ thị của hàm số có đáp án
20 câu hỏi
I. Nhận biết
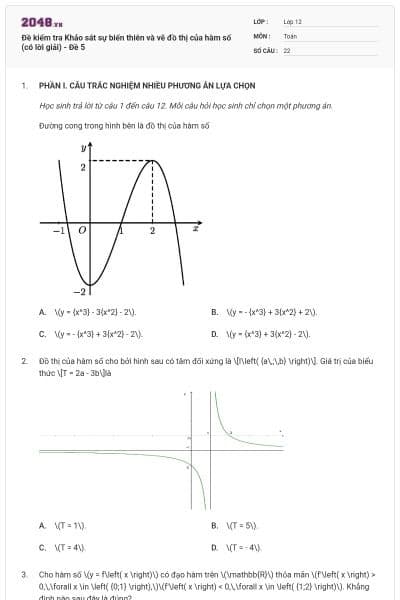
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
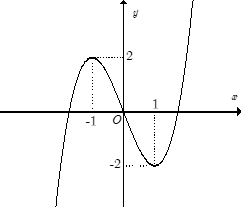
y = x3 – 3x.
y = −x3 + 3x.
y = −x4 + 2x2.
y = x4 − 2x2.
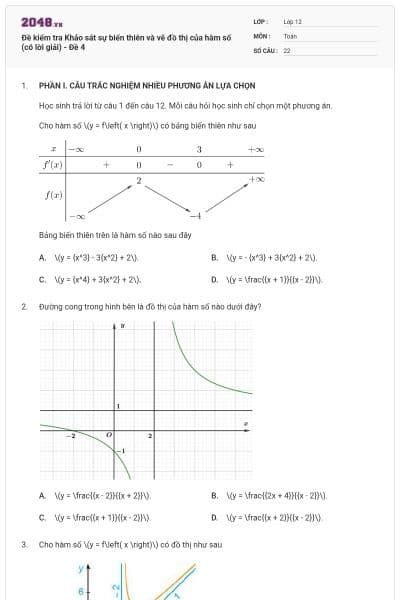
Đường cong trong hình vẽ bên là đồ thị hàm số nào dưới đây?
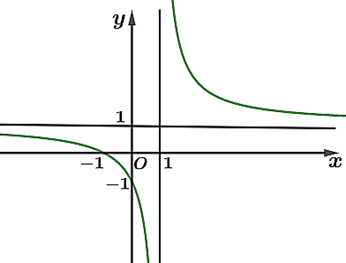
\(y = {x^3} - 3x - 1\).
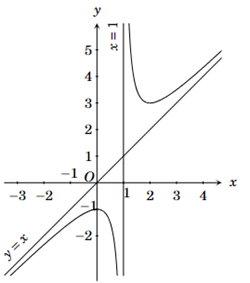
\(y = \frac{{2x - 1}}{{x - 1}}\).
\(y = \frac{{x + 1}}{{x - 1}}\).
\(y = {x^4} + {x^2} + 1\).
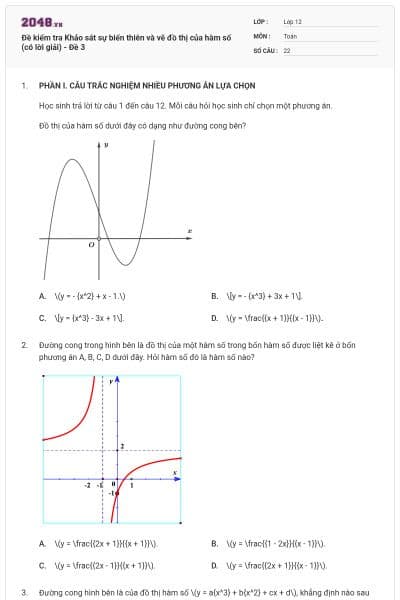
Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây?
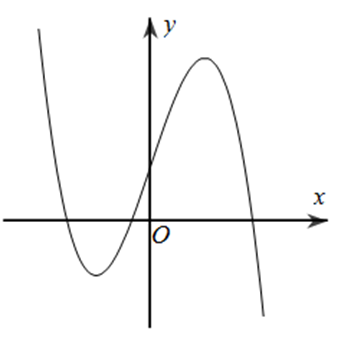
\(y = \frac{{x + 2}}{{x - 1}}\).
\(y = - {x^3} + 3x + 1\).
\(y = - {x^4} + x + 1\).
\(y = {x^3} + 3x + 1\).
Tâm đối xứng của đồ thị hàm số \(y = {x^3} + 1\) là
\(C(1;\,\,2).\)
\(O(0\,;\,\,0).\)
\(A(0;\,\,1).\)
\(B(1;\,\,1).\)
Xác định tâm đối xứng của đồ thị hàm số sau
\(C(1;\,\,2).\)
\(O(0\,;\,\,0).\)
\(A(0;\,\,1).\)
\(B(1;\,\,1).\)
II. Thông hiểu
Cho hàm số y = f(x) = ax3 + bx2 + cx + d có bảng biến thiên sau:
Đồ thị nào trong các phương án A, B, C, D thể hiện hàm số y = f(x)?
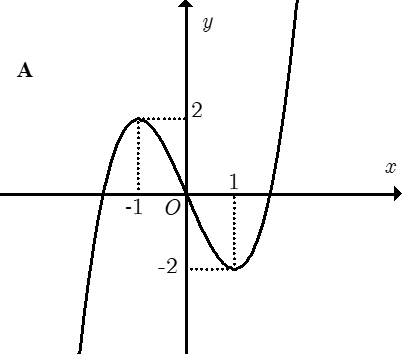
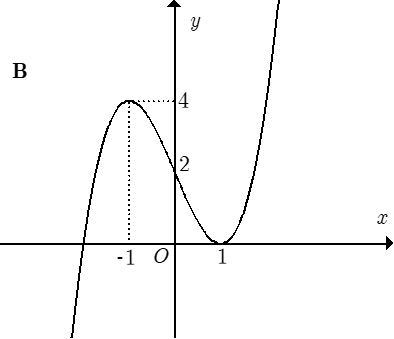
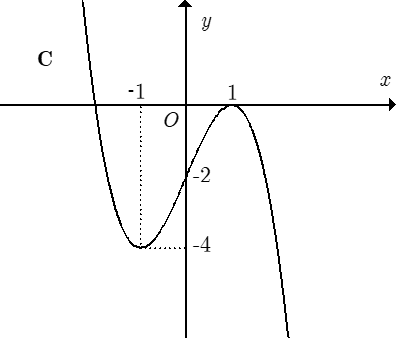
Trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hàm số nào có bảng biến thiên như sau?
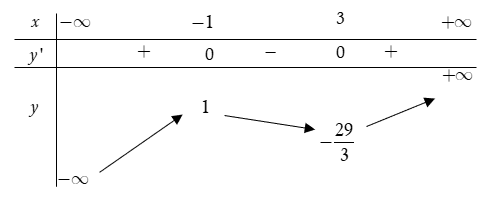
y = −x3 + 3x2 + 9x – 2.
\(y = \frac{1}{3}{x^3} - {x^2} - 3x - \frac{2}{3}\) .
y = x3 − 3x2 − 9x – 2.
\(y = - \frac{1}{3}{x^3} + {x^2} + 3x + \frac{2}{3}\).
Biết rằng hàm số y = f(x) = ax3 + bx2 + cx + d (a ≠ 0) có đồ thị là một trong các dạng dưới đây:
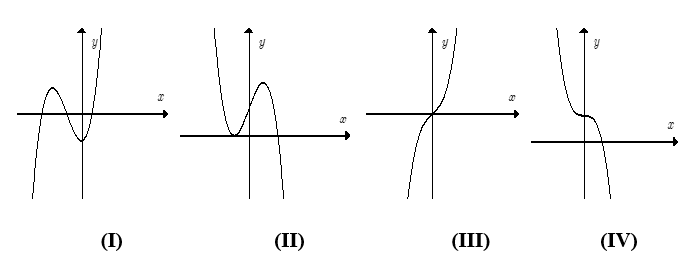
Mệnh đề nào sau đây là đúng?
Đồ thị (I) xảy ra khi a < 0 và f'(x) = 0 có hai nghiệm phân biệt.
Đồ thị (II) xảy ra khi a > 0 và f'(x) = 0 có hai nghiệm phân biệt.
Đồ thị (III) xảy ra khi a > 0 và f'(x) = 0 vô nghiệm hoặc có nghiệm kép.
Đồ thị (IV) xảy ra khi a > 0 và f'(x) = 0 có có nghiệm kép.
Bảng biến thiên trong hình dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
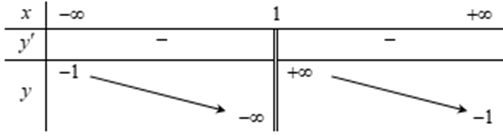
\(y = \frac{{x + 3}}{{x - 1}}\).
\(y = \frac{{ - x - 2}}{{x - 1}}\).
\(y = \frac{{ - x + 3}}{{x - 1}}\).
\(y = \frac{{ - x - 3}}{{x - 1}}\).
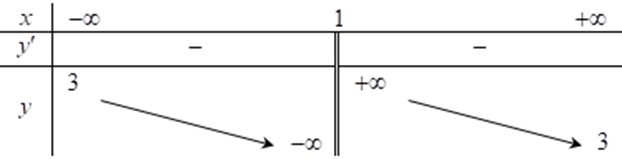
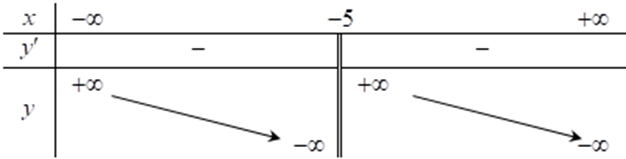
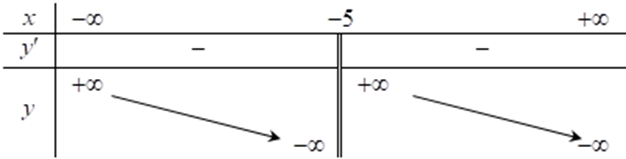
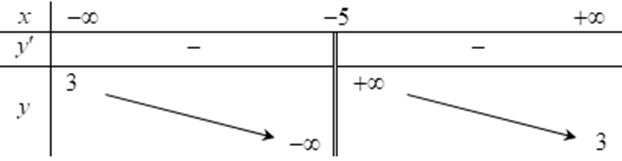
Hàm số \(y = \frac{{3x + 2}}{{x - 1}}\) có bảng biến thiên nào dưới đây. Chọn đáp án đúng?
Cho hàm số \[y = \frac{{ax - b}}{{x - 1}}\] có đồ thị như hình vẽ dưới đây:
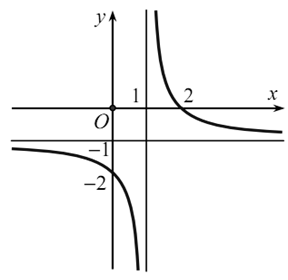
Khẳng định nào sau đây đúng?
\(b < a < 0\).
\(a < b < 0\).
\(b > a\)và \(a < 0\).
\(a < 0 < b\).
Bảng biến thiên sau là của hàm số nào?
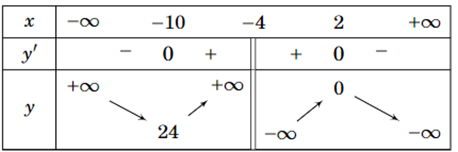
\(y = \frac{{{x^2} - 3x + 4}}{{ - x - 4}}\).
\(y = \frac{{{x^2} - 4x + 4}}{{ - x - 4}}\).
\(y = \frac{{{x^2} - 5x + 4}}{{x + 4}}\).
\(y = \frac{{{x^2} - 4x + 4}}{{x + 4}}\).
Bảng biến thiên sau là của đồ thị hàm số nào
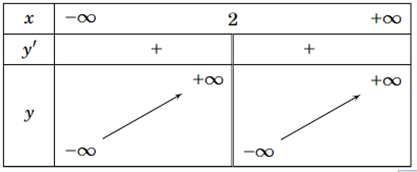
\(y = \frac{{{x^2} - 3}}{{x - 2}}\).
\(y = \frac{{{x^2} - 4x + 2}}{{x - 2}}\).
\(y = \frac{{{x^2} - x}}{{x - 2}}\).
\(y = \frac{{{x^2} - 4x + 5}}{{x - 2}}\).
Đồ thị hàm số ở hình sau là của hàm số nào
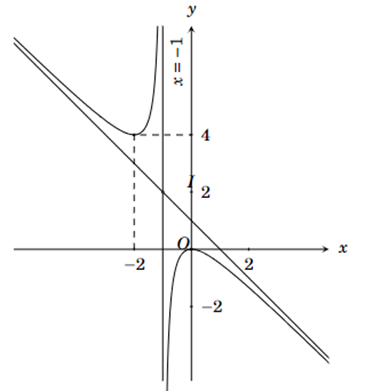
\(y = \frac{{{x^2} - x}}{{x + 1}}\).
\(y = \frac{{{x^2} - 3x}}{{x + 1}}\).
\(y = \frac{{{x^2} + x + 2}}{{x + 1}}\).
\(y = \frac{{ - {x^2}}}{{x + 1}}\).
Đồ thị hàm số ở hình sau là của hàm số nào.
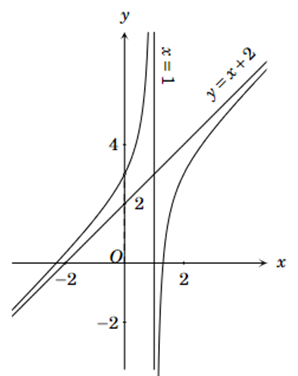
\(y = \frac{{{x^2} + 3}}{{x - 1}}\).
\(y = \frac{{{x^2} + x - 3}}{{x - 1}}\).
\(y = \frac{{{x^2} - 2x + 3}}{{ - x + 1}}\).
\(y = \frac{{{x^2} + 3}}{{ - x + 1}}\).
III. Vận dụng
Cho hàm số \[y = {x^3} + (m + 3){x^2} + 1 - m\] với \(m\) là tham số. Giả sử tồn tại giá trị nào đó của tham số \(m\) thì đồ thị hàm đi qua gốc tọa độ, khi đó mệnh đề nào sau đây sai?
Đồ thị hàm số cắt trục tung tại một điểm.
Đồ thị hàm số tiếp xúc với trục hoành.
Đồ thị hàm số cắt trục hoành tại hai điểm phân biệt.
Đồ thị hàm số cắt trục hoành tại ba điểm phân biệt.
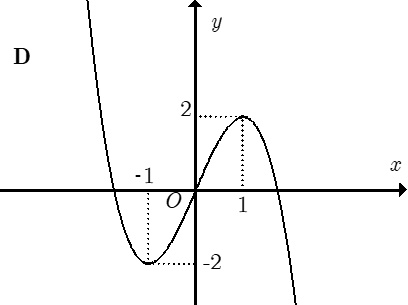
Cho hàm số y = ax3 + bx2 + cx + d có đồ thị như hình vẽ bên dưới.
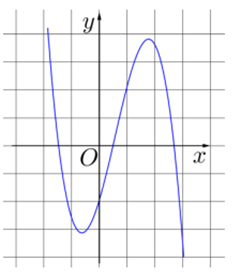
Mệnh đề nào dưới đây đúng?
a < 0, b > 0, c > 0, d < 0.
a < 0, b < 0, c > 0, d
a > 0, b < 0, c < 0, d > 0.
a < 0, b > 0, c < 0, d < 0.
Cho hàm số \[y = \frac{{ax + b}}{{cx + d}}\] có đồ thị như trong hình bên dưới. Biết rằng \[a\] là số thực dương, hỏi trong các số \[b,\,\,c,\,\,d\] có tất cả bao nhiêu số dương?
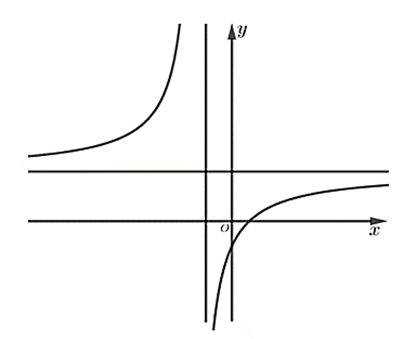
\[1\].
\[2\].
\[0\].
\[3\].
Xác định \(a,\,b,\,c\) để hàm số \(y = \frac{{ax - 1}}{{bx + c}}\) có đồ thị như hình vẽ bên. Chọn đáp án đúng?
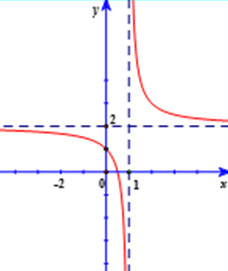
\(a = 2,\,\,b = - 1,\,c = 1.\)
\(a = 2,\,\,b = 1,\,c = 1.\)
\(a = 2,\,\,b = 2,\,c = - 1.\)
\(a = 2,\,\,b = 1,\,c = - 1.\)
Tọa độ điểm M thuộc đồ thị (C) của hàm số \(y = \frac{{2x - 1}}{{x - 1}}\) sao cho khoảng cách từ điểm M đến tiệm cận đứng bằng 1 là
M(0; 1), M(2; 3).
M(2; 1).
\(M\left( { - 1;\frac{3}{2}} \right)\).
\(M\left( {3;\frac{5}{2}} \right)\).