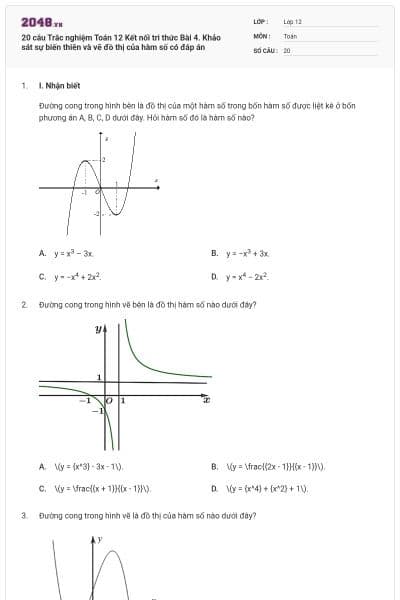
Đề kiểm tra Khảo sát sự biến thiên và vẽ đồ thị của hàm số (có lời giải) - Đề 4
22 câu hỏi
PHẦN I. CÂU TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN
Học sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi học sinh chỉ chọn một phương án.
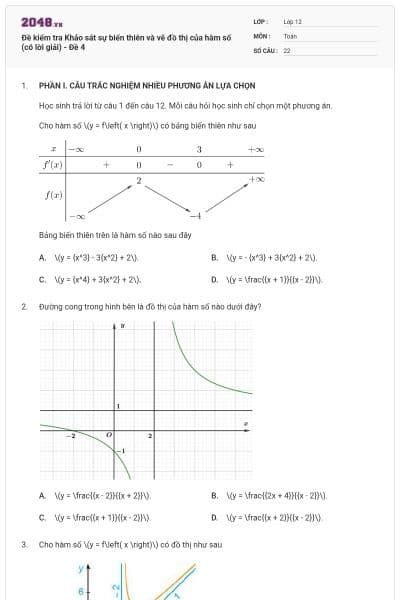
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
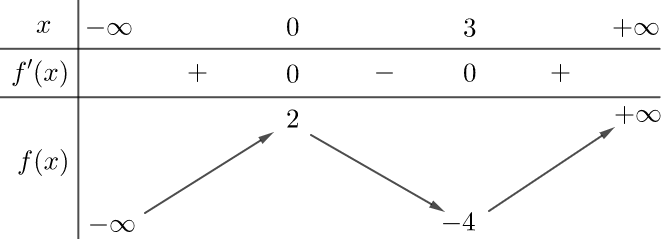
Bảng biến thiên trên là hàm số nào sau đây
\(y = {x^3} - 3{x^2} + 2\).
\(y = - {x^3} + 3{x^2} + 2\).
\(y = {x^4} + 3{x^2} + 2\).
\(y = \frac{{x + 1}}{{x - 2}}\).
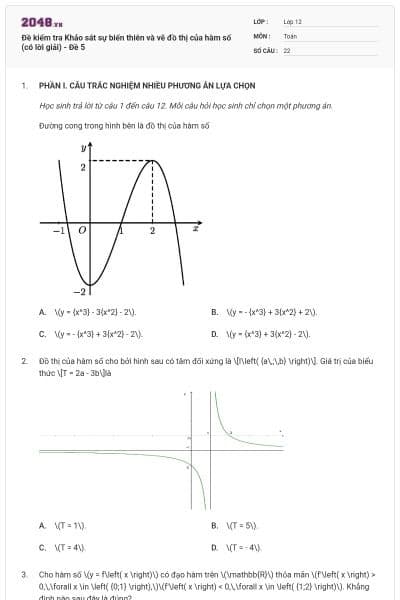
Đường cong trong hình bên là đồ thị của hàm số nào dưới đây?
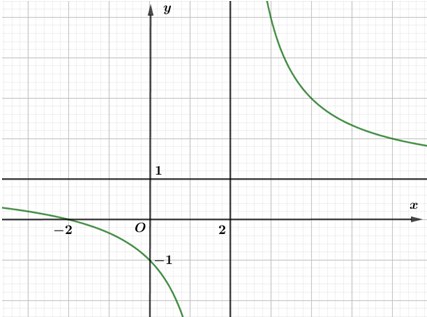
\(y = \frac{{x - 2}}{{x + 2}}\).
\(y = \frac{{2x + 4}}{{x - 2}}\).
\(y = \frac{{x + 1}}{{x - 2}}\).
\(y = \frac{{x + 2}}{{x - 2}}\).
Cho hàm số \(y = f\left( x \right)\) có đồ thị như sau
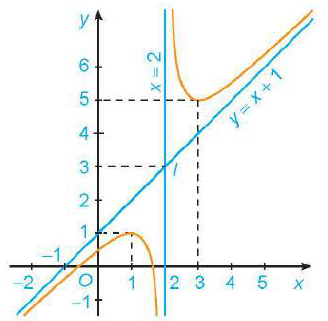
Khẳng định nào sau đây SAI?
Đồ thị hàm số có tiệm cận đứng \(x = 2\).
Đồ thị hàm số có tiệm cận xiên \(y = x + 1\).
\(\mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\mathop {\lim }\limits_{x \to - \infty } y = - \infty \).
Tọa độ giao điểm của đồ thị và trục \(Ox\) là \(A\left( {0;1} \right)\).
Đường cong trong hình bên là đồ thị của hàm số nào dưới đây?
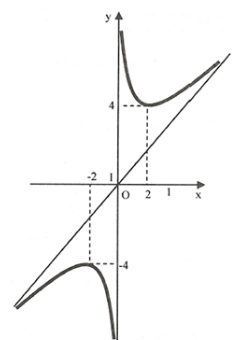
\(y = \frac{{x - 1}}{{x + 1}}\).
\(y = {x^4} - 2{x^2}\).
\(y = \frac{{{x^2} + 4}}{x}\).
\(y = {x^3} - 3{x^2}\).
Cho hàm số \[y = \frac{{2x - 4}}{{x - 1}}\] . Tọa độ giao điểm của đồ thị và trục \[Oy\] là
\(\left( {2;0} \right)\).
\(\left( {0;2} \right)\).
\(\left( {4;0} \right)\).
\(\left( {0;4} \right)\).
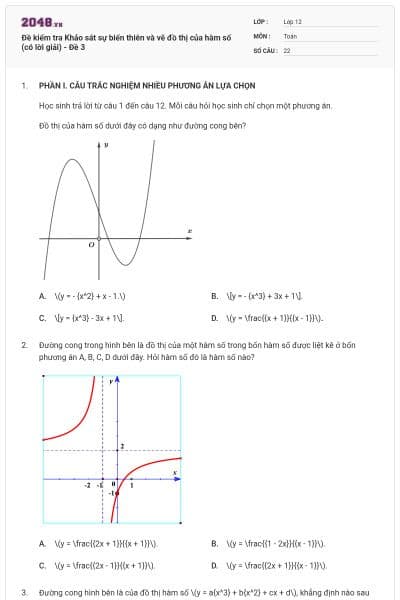
Đường cong trong hình bên là đồ thị của hàm số nào dưới đây?
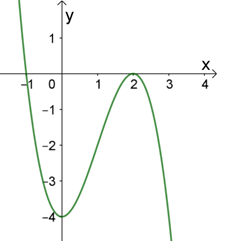
\(y = \frac{{x - 1}}{x}\).
\(y = {x^3} + 3{x^2} - 4\).
\(y = - {x^3} + 3x - 4\).
\(y = - {x^3} + 3{x^2} - 4\).
Cho hàm số \[y = \frac{{{x^2} + 2x - 1}}{{x - 1}}\] và \[y = 2x - 7\]. Hai đồ thị cắt nhau tại hai điểm thì tổng hoành độ hai giao điểm bằng
\(7\).
\(5\).
\(8\).
\(11\).
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ { - 1} \right\}\), liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình sau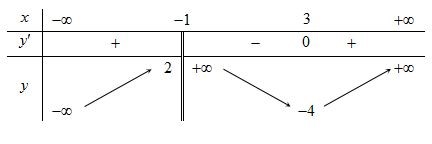
Số giao điểm của đường thẳng \(y = 1\) và đồ thị của hàm số \(y = f\left( x \right)\) là
\(3\).
\(2\).
\(1\).
\(0\).
Cho hàm số \(y = \frac{{\left( {a - 1} \right)x + b}}{{\left( {c - 1} \right)x + d}},\,\,d < 0\) có đồ thị như hình trên. Khẳng định nào dưới đây là đúng?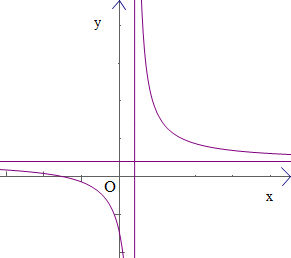
\(a > 1,\,b > 0,\,c < 1\).
\(a > 1,\,b < 0,\,c > 1\).
\(a < 1,\,b > 0,\,c < 1\).
\(a > 1,\,b > 0,\,c > 1\).
Một công ty chuyên sản xuất thùng phi nhận được đơn đặt hàng với yêu cầu là thùng phi phải có dạng hình trụ và chứa được \(16\pi \left( {{m^3}} \right)\) mỗi chiếc. Hỏi chiếc thùng phải có chiều cao \[h\] và bán kính đáy \[R\]bằng bao nhiêu để sản xuất ít tốn vật liệu nhất?
\(R = 4\left( m \right),h = 2\left( m \right)\).
\(R = 2\left( m \right),h = 4\left( m \right)\).
\(R = 2\left( m \right),h = 2\left( m \right)\).
\(R = 4\left( m \right),h = 4\left( m \right)\).
Gọi \(S\) là tập hợp các giá trị \(m\) để tiệm cận xiên của đồ thị hàm số \(y = \frac{{m{x^2} + x - 3}}{{x - 1}}\) tạo với hai trục hệ tọa độ \(Oxy\) một tam giác có diện tích bằng \(2\). Khi đó tổng các giá trị của \(S\) bằng
\(\frac{7}{2}\).
\( - \frac{3}{2}\).
\(\frac{5}{2}\).
Một bể ban đầu chứa \(150\) lít nước. Sau đó, cứ mỗi phút người ta bơm thêm \(50\) lít nước, đồng thời cho vào bể \(20\) gam chất khử trùng ( hòa tan ). Đặt \(f\left( t \right)\) gam/lít là nồng độ chất khử trùng trong bể sau \(t\) phút ( \(t \ge 0\)), biết rằng sau khi khảo sát sự biến thiên của hàm số \(f\left( t \right)\), ta thấy giá trị \(f\left( t \right)\) tăng theo \(t\) nhưng không vượt ngưỡng \(p\) gam/lít. Tìm số \(p\) ( kết quả thể hiện dưới dạng số thập phân ).
\(p = 0,4\).
\(p = 0,3\).
\(p = 0,2\).
\(p = 0,1\).
PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI
Học sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, học sinh chọn đúng hoặc sai.
Cho hàm số \[y = {x^3} - 3x + 2\]. Khi đó
a) Tập xác định của hàm số đã cho là \[\left( {0\,;\, + \infty } \right)\].
b) Đồ thị của hàm số đã cho đi qua điểm \[\left( {0\,;2} \right)\].
c) Hàm số đạt cực trị tại \[x = 0\].
d) Giá trị lớn nhất của hàm số đã cho trên đoạn \[\left[ {0;2} \right]\] bằng \[4\].
Cho đồ thị hàm số \[y = \frac{{bx - c}}{{x - a}}\] (\[a,b,c \in \mathbb{R}\]) có đồ thị như hình vẽ bên dưới.
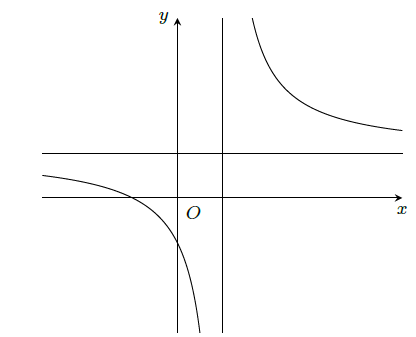
a) Hàm số nghịch biến trên từng khoảng xác định.
b) Giao điểm với trục tung là điểm có tung độ âm.
c) Giao điểm với trục hoành là điểm có hoành độ âm.
d) Trong các số \[a,b,c\] có hai số âm.
Cho hàm số \[y = \frac{{{x^2} - 2x + 4}}{{x - 2}}\] có đồ thị \[\left( C \right)\]. Khi đó
a) Tập xác định của hàm số đã cho là \[\mathbb{R}\].
b) Đồ thị hàm số có tiệm cận đứng là đường thẳng \[x = 2\] và có tiệm cận xiên là đường thẳng \[y = x\].
c) Tổng giá trị cực đại và giá trị cực tiểu của hàm số đã cho bằng \[4\].
d) Cho đường thẳng \[y = mx - 2\]. Khi đó có đúng 8 giá trị nguyên của tham số \[m\] không vượt quá 10 để đồ thị hàm số đã cho cắt đường thẳng \[y = mx - 2\] tại hai điểm phân biệt nằm về hai phía so với tiệm cận đứng của đồ thị \[\left( C \right)\].
Cho hàm số \[y = x - \frac{1}{{x + 1}}\] có đồ thị là \[\left( C \right)\].
a) Đồ thị hàm số có tiệm cận đứng là \[x = 1\].
b) Phương trình tiếp tuyến của đồ thị \[\left( C \right)\] tại điểm điểm có hoành độ \[M\left( {0; - 1} \right)\] là \[y = 2x - 1\].
c) Tồn tại tiếp tuyến của đồ thị vuông góc với nhau.
d) Để đường thẳng \[y = k\] cắt \[\left( C \right)\] tại hai điểm phân biệt \[A,B\] sao cho \[OA \bot OB\] thì \[k\] là nghiệm của phương trình \[{k^2} - k - 1 = 0\].
PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN
Học sinh trả lời từ câu 1 đến câu 6
Cho hàm số \(y = {x^3} - 3{x^2} + 2\). Giá trị cực tiểu của hàm số đã cho bằng bao nhiêu?
Cho hàm số \(y = \frac{{5x - 3}}{{2x + 6}}\). Đồ thị hàm số có đường tiệm cận đứng và ngang lần lượt là các đường thẳng \(x = a\) và \(y = b\). Tính \(a + 4b?\)
Cho đồ thị hàm số \(f(x) = \frac{{5{x^2} - 6x + 9}}{{x - 1}}\) có tâm đối xứng là \(I(a\,;\,b)\). Giá trị của biểu thức \(C = a + 3b\) là bao nhiêu?
Cho hàm số\[y = {x^3} - 3x + 2\] có đồ thị \[\left( C \right)\] và \(y = \frac{{x + 2}}{{x - 1}}\) có đồ thị \[\left( T \right)\]. Số giao điểm của \[\left( C \right)\] với \[\left( T \right)\] là?
Cho hàm số \(y = f(x) = {2024^x} - {2024^{ - x}} + x + \sin x\). Có bao nhiêu giá trị nguyên của tham số m để phương trình \(f(x + 3) + f\left( {{x^3} - 4x + m} \right) = 0\) có đúng ba nghiệm phân biệt?
Một cốc chứa \[25\]ml dung dịch \[NaOH\]với nồng độ \[100\] mg/ml. Một bình chứa dung dịch \[NaOH\] khác với nồng độ \[9\]mg/ml được trộn vào cốc. Gọi \[C\left( x \right)\] là nồng độ của \[NaOH\] sau khi trộn \[x\](ml) từ bình chứa, ta thấy nồng độ của \[NaOH\]trong cốc sẽ luôn giảm theo \[x\] nhưng luôn lớn hơn một số \[a\]. Tính \[a\]?