Đề kiểm tra Công thức lượng giác (có lời giải) - Đề 3

Gọi \(M = \tan x - \tan y\) thì:              

Nếu \({\mathop{\rm s}\nolimits} {\rm{inx}} + \cos x = \frac{1}{2}\) thì \(\sin 2x\) bằng             

Biểu thức \[\frac{{1 + \sin 4\alpha - cos4\alpha }}{{1 + \sin 4\alpha + cos4\alpha }}\] có kết quả rút gọn bằng:              

Biết \[\sin x = \frac{1}{3}\] và \({90^0} < x < {180^0}\)thì biểu thức \(\frac{{1 + \sin 2x + \cos 2x}}{{1 + \sin 2x - \cos 2x}}\) có giá trị bằng:              

Rút gọn biểu thức \(P = \cos \left( {120^\circ + x} \right) + \cos \left( {120^\circ - x} \right) - \cos x\) ta được kết quả là:              

Nếu \[\sin a - \cos a = \frac{1}{5}({135^0} < a < {180^0})\] thì giá trị đúng của \[\tan 2a\] là:

Nếu biết  $\mathrm{tan\alpha }=\frac{1}{2}(0<\mathrm{a}<90°),\mathrm{tanb}=-\frac{1}{3}({90}^{°}<\mathrm{b}<{180}^{°})$ thì\[{\rm{cos(2a - b)}}\]có giá trị đúng bằng:              

Giá trị lớn nhất của \(M = {\sin ^4}x + {\cos ^4}x\) bằng              

Giá trị nhỏ nhất của \(M = {\sin ^4}x + {\cos ^4}x\)là              

Một tam giác \(ABC\) có các góc \(A,\,B,\,C\) thỏa mãn \(\sin \frac{A}{2}{\cos ^3}\frac{B}{2} - \sin \frac{B}{2}{\cos ^3}\frac{A}{2} = 0\)                thì tam giác đó có gì đặc biệt?             

Trong các hệ thức sau, hệ thức nào sai?              

Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Biết \(\sin a = \frac{8}{{17}},\tan b = \frac{5}{{12}}\) và \(a\), \(b\) là các góc nhọn. Khi đó:

a) \(\tan a = \frac{8}{{15}}\)

b) \(\sin (a - b) = \frac{{21}}{{221}}\)

c) \(\cos (a + b) = \frac{{14}}{{22}}\)

d) \(\tan (a + b) = \frac{{17}}{{14}}.\)

Biết \(0 < a,b < \frac{\pi }{2},a + b = \frac{\pi }{4}\) và \(\tan a\tan b = 3 - 2\sqrt 2 \). Khi đó:

a) \(\tan a + \tan b = - 2 + 2\sqrt 2 {\rm{. }}\)

b) \(\tan a = - 1 + \sqrt 2 \)

c) \(\tan b = - 1 - \sqrt 2 \)

d) \(\tan a - \tan b = - 2 - 2\sqrt 2 {\rm{. }}\)

Biết: \(\sin \alpha = \frac{1}{3}\) và \(0 < \alpha < \frac{\pi }{2}\). Khi đó:

a) \(\sin 2\alpha = \frac{{\sqrt 2 }}{9}\)

b) \(\cos 2\alpha = \frac{7}{9}\)

c) \(\tan 2\alpha = \frac{{\sqrt 2 }}{7}\)

d) \(\cot 2\alpha = \frac{{7\sqrt 2 }}{2}\)

Biết: $\cos 2\alpha =\frac{5}{9},0^{°}<\alpha <{90}^{°}$. Khi đó:

a) \(\sin \alpha = \frac{{\sqrt {28} }}{9}\)

b) \(\cos \alpha = \frac{{\sqrt {53} }}{9}\)

c) \(\tan \alpha = \frac{{\sqrt {371} }}{{53}}\)

d) \(\cot \alpha = \frac{{\sqrt {371} }}{{14}}\)

Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.

Cho \(\sin \alpha = - \frac{1}{3}\), với $\left({180}^{°}<\alpha <{270}^{°}\right)$. Tính \(\cos \alpha \).

Cho hai góc nhọn \(a\) và \(b\) với \(\tan a = \frac{1}{7}\) và \(\tan b = \frac{3}{4}\). Tính \(a + b\).

Biến đổi thành tổng biểu thức \(\sin x\sin 2x\sin 3x\).

Rút gọn biểu thức sau: \(A = \frac{{\sin x + \sin 2x + \sin 3x + \sin 4x}}{{\cos x + \cos 2x + \cos 3x + \cos 4x}}\)

Một thiết bị trễ kĩ thuật số lặp lại tín hiệu đầu vào bằng cách lặp lại tín hiệu đó trong một khoảng thời gian cố định sau khi nhận được tín hiệu. Nếu một thiết bị như vậy nhận được nốt thuần \({f_1}(t) = 5\sin t\) và phát lại được nốt thuần \({f_2}(t) = 5\cos t\) thì âm kết hợp là \(f(t) = {f_1}(t) + {f_2}(t)\), trong đó \(t\) là biến thời gian. Chứng tỏ rằng âm kết hợp viết được dưới dạng \(f(t) = k\sin (t + \varphi )\), tức là âm kết hợp là một sóng âm hình sin. Hãy xác định biên độ âm \(k\) và pha ban đầu \(\varphi ( - \pi \le \varphi \le \pi )\) của sóng âm.

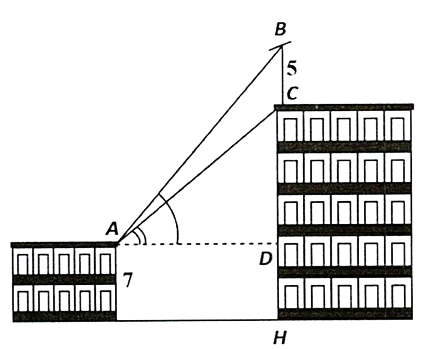
Trên nóc một tòa nhà có một cột ăng-ten cao \(5\;m\). Từ vị trí quan sát \(A\) cao \(7\;m\) so với mặt đất, có thể nhìn thấy đỉnh \(B\) và chân \(C\) của cột ăng-ten dưới góc \(\alpha \) và \(\beta \) so với phương nằm ngang. Biết chiều cao của toà nhà là \(18,9\;m\), hai toà nhà cách nhau \(10\;m\).

a) Tính \(\tan \alpha \);                             b) Tính góc \(\alpha \)