Đề kiểm tra Công thức lượng giác (có lời giải) - Đề 2
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Rút gọn biểu thức \(\cos (x + \frac{\pi }{4}) - \cos (x - \frac{\pi }{4})\) ta được
\(\sqrt 2 \sin x\).
\( - \sqrt 2 \sin x\).
\(\sqrt 2 \cos x\).
\( - \sqrt 2 \cos x\).
Giá trị của biểu thức \(\cos \frac{{37\pi }}{{12}}\) bằng
\(\frac{{\sqrt 6 + \sqrt 2 }}{4}\).
\(\frac{{\sqrt 6 - \sqrt 2 }}{4}\).
–\(\frac{{\sqrt 6 + \sqrt 2 }}{4}\).
\(\frac{{\sqrt 2 - \sqrt 6 }}{4}\).
Biểu thức \[M = \cos \left( { - 53^\circ } \right).\sin \left( { - 337^\circ } \right) + \sin \left( {307^\circ } \right).\sin \left( {113^\circ } \right)\] có giá trị bằng:
\( - \frac{1}{2}\).
\(\frac{1}{2}\).
\( - \frac{{\sqrt 3 }}{2}\).
\(\frac{{\sqrt 3 }}{2}\).
Gọi \(M = {\cos ^4}{15^{\rm{o}}} - {\sin ^4}{15^{\rm{o}}}\) thì:
\(M = 1.\)
\(M = \frac{{\sqrt 3 }}{2}.\)
\(M = \frac{1}{4}.\)
\(M = 0.\)
Giá trị đúng của \(\cos \frac{{2\pi }}{7} + \cos \frac{{4\pi }}{7} + \cos \frac{{6\pi }}{7}\) bằng
\(\frac{1}{2}\).
\( - \frac{1}{2}\).
\(\frac{1}{4}\).
–\(\frac{1}{4}\).
Biết \(\sin \alpha = \frac{{\sqrt 3 }}{2}\) và \(\frac{\pi }{2} < \alpha < \pi \). Giá trị của \(P = \cos \left( {2\alpha - \frac{\pi }{3}} \right)\) là
\(P = 0\).
\(P = - 1\).
\(P = \frac{1}{2}\).
\(P = - \frac{{\sqrt 3 }}{2}\).
Khi \[\alpha = \frac{\pi }{6}\] thì biểu thức \[\frac{{si{n^2}2\alpha + 4si{n^4}\alpha - 4{{\sin }^2}\alpha .{{\cos }^2}\alpha }}{{4 - {{\sin }^2}2\alpha - 4{{\sin }^2}\alpha }}\] có giá trị bằng.
\[\frac{1}{3}\].
\[\frac{1}{6}\].
\[\frac{1}{9}\].
\[\frac{1}{{12}}\].
Cho biểu thức Hãy chọn kết quả đúng
\[A = 2\cos a.\sin b.\sin \left( {a + b} \right).\]
\[A = 2\sin a.\cos b.\cos \left( {a + b} \right).\]
\[A = 2\cos a.\cos b.\cos \left( {a + b} \right).\]
\[A = 2\sin a.\sin b.\cos \left( {a + b} \right).\]
Biết \(\cot x = \frac{3}{4},\,\cot y = \frac{1}{7}\), \(x,\,y\) đều là góc dương, nhọn thì:
\(x + y = \frac{\pi }{4}\).
\(x + y = \frac{{2\pi }}{3}\).
\(x + y = \frac{{3\pi }}{4}\).
\(x + y = \frac{{5\pi }}{6}\)
Nếu biết \(\left\{ \begin{array}{l}\tan a + \tan b = 2\\\tan \left( {a + b} \right) = 4\end{array} \right.\) thì các giá trị của \(\tan a,\,\tan b\) bằng:
\(\frac{1}{3},\,\frac{5}{3}\) hoặc ngược lại.
\(\frac{1}{2},\,\frac{3}{2}\) hoặc ngược lại.
\(1 - \frac{{\sqrt 3 }}{2},\,1 + \frac{{\sqrt 3 }}{2}\) hoặc ngược lại.
\(1 - \frac{{\sqrt 2 }}{2},\,1 + \frac{{\sqrt 2 }}{2}\) hoặc ngược lại.
Hãy xác định hệ thức sai:
\(\sin x.{\cos ^3}x - \cos {\rm{ }}x{\sin ^3}x = \frac{{\sin 4x}}{4}\).
\({\sin ^4}x + {\cos ^4}x = \frac{{3 + \cos 4x}}{4}\).
\(\frac{{1 + \sin x}}{{{\rm{cos }}x}} = \cot \left( {\frac{\pi }{4} + \frac{x}{2}} \right)\).
\({\cot ^2}x + {\tan ^2}x = \frac{{2\cos 4x + 6}}{{1 - \cos 4x}}\).
Trong các hệ thức sau, hệ thức nào sai?
\(\sin \left( {x + \frac{\pi }{6}} \right).{\rm{cos}}\left( {x - \frac{\pi }{6}} \right) = \frac{{2{\mathop{\rm s}\nolimits} {\rm{in2x + }}\sqrt 3 }}{4}\).
\(\sin \frac{\pi }{5}.\sin \frac{{2\pi }}{5} = \frac{1}{2}\left( {{\rm{cos}}\frac{\pi }{5}{\rm{ + cos}}\frac{{2\pi }}{5}} \right)\).
\(\sin \left( {x + \frac{\pi }{6}} \right).\sin \left( {x - \frac{\pi }{6}} \right).\,{\rm{ }}\cos 2x = \frac{1}{4}{\rm{ }}\cos 2x - \frac{1}{8}{\rm{ }}\cos 4x\, - \frac{1}{8}\).
\(8\cos x.\sin 2x.\sin 3x = 2\left( {\cos 2x - \cos 4x - \cos 6x\, + \,1} \right)\).
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho biết \(\sin x = \frac{1}{{\sqrt 3 }}\) và \(0 < x < \frac{\pi }{2}\); khi đó:
a) \(\cos x > 0\)
b) \(\cos x = \frac{{\sqrt 6 }}{3}\)
c) \(\tan x = \frac{{\sqrt 3 }}{3}\)
d) \(\cos \left( {x + \frac{\pi }{3}} \right) = \frac{{\sqrt 6 - 3}}{8}{\rm{. }}\)
Cho biết \(\cos x = - \frac{{12}}{{13}}\) và \(\pi < x < \frac{{3\pi }}{2}\); khi đó:
a) \(\sin x > 0\)
b) \(\sin x = - \frac{5}{{13}}\)
c) \(\cot x = \frac{5}{{12}}\)
d) \(\sin \left( {\frac{\pi }{3} - x} \right) = \frac{{5 - 12\sqrt 3 }}{{26}}\)
Biết \(\sin 2\alpha = - \frac{4}{5},\frac{\pi }{2} < \alpha < \frac{{3\pi }}{2}\). Khi đó:
a) \(\cos \alpha < 0\)
b) \(2\sin \alpha \cos \alpha = - \frac{4}{5}\)
c) \(\cos \alpha = \frac{{ - 2}}{{\sqrt 5 }},\sin \alpha = \frac{1}{{\sqrt 5 }}\)
d) \(\cos \alpha = \frac{{ - 1}}{{\sqrt 5 }},\sin \alpha = - \frac{2}{{\sqrt 5 }}\)
Cho \(\sin \alpha = \frac{2}{3},\frac{\pi }{2} < \alpha < \pi \). Khi đó:
a) \(\cos \alpha = - \frac{{\sqrt 5 }}{3}\)
b) \(\tan \alpha = - \frac{{2\sqrt 5 }}{5}\)
c) \(\cos \left( {\frac{\pi }{3} + \alpha } \right) = \frac{{\sqrt 5 - 2\sqrt 3 }}{6}\)
d) \(\cos \left( {\frac{\pi }{4} - \alpha } \right) = \frac{{\sqrt {10} - 2\sqrt 2 }}{6}\)
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Cho \(\sin \alpha = \frac{3}{5}\) và . Tính \(\cos \alpha \).
Cho hai góc nhọn \(a\) và \(b\). Biết \(\cos a = \frac{1}{3};\cos b = \frac{1}{4}\). Tính giá trị của biểu thức:
\(P = \cos (a + b)\cos (a - b){\rm{. }}\)
Biến đổi thành tổng biểu thức sau: \(4\sin 3x\sin 2x\cos x\).
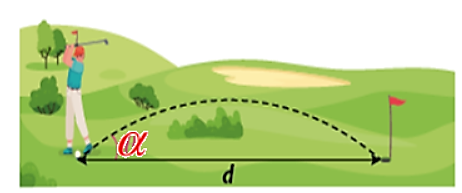
Một quả bóng golf kể từ lúc được đánh đến lúc chạm đất đã di chuyển được một khoảng cách \(d\left( m \right)\) theo phương nằm ngang. Biết rằng \(d = \frac{{{v_0}^2\sin 2\alpha }}{g}\) trong đó\({v_0}\left( {m/s} \right)\) là vận tốc ban đầu của quả bóng, \(g\left( {m/{s^2}} \right)\) là gia tốc trọng trường và \(\alpha \)là góc đánh quả bóng so với phương nằm ngang. Tính khoảng cách \(d\) biết rằng \({v_0} = 15\left( {m/s} \right);\)\(g = 10\left( {m/{s^2}} \right)\) và \[{\rm{cos}}\alpha = \frac{3}{5}\] với \[\left( {0 \le \alpha \le {{45}^0}} \right)\].
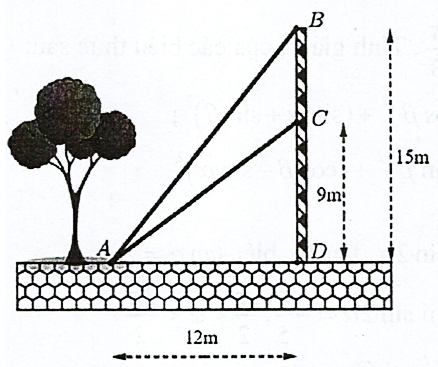
Từ một vị trí \(A\), người ta buộc hai sợi cáp \(AB\) và \(AC\) đến một cái trụ cao \(15\;m\), được dựng vuông góc với mặt đất, chân trụ ở vị trí \(D\). Biết \(CD = 9\;m\) và \(AD = 12\;m\). Tìm góc nhọn \(\alpha = \widehat {BAC}\) tạo bởi hai sợi dây cáp đó, đồng thời tính gần đúng \(\alpha \) (làm tròn đến hàng phần chục, đơn vị độ).
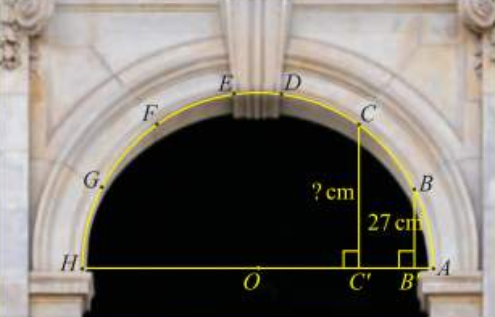
Trong kiến trúc, các vòm cổng bằng đá thường có hình nửa đường tròn để có thể chịu lực tốt. Trong hình bên, vòm cổng được ghép bởi sáu phiến đá hai bên tạo thành các cung AB,BC,CD,EF,FG,GH bằng nhau và một phiến đá chốt ở đỉnh. Biết chiều rộng cổng là \(120\,{\rm{cm}}\) và khoảng cách từ \(B\) đến đường kính \(AH\) bằng \(27\,{\rm{cm}}\). Tính khoảng cách từ \(C\)đến \(AH\).