22 câu trắc nghiệm Toán 11 Kết nối tri thức Bài 2: Công thức lượng giác có đáp án
22 câu hỏi
Khẳng định nào sau đây đúng?
\(\sin \left( {2018a} \right) = 2018\sin a.\cos a.\)
\(\sin \left( {2018a} \right) = 2018\sin \left( {1009a} \right).\cos \left( {1009a} \right).\)
\(\sin \left( {2018a} \right) = 2\sin a\cos a.\)
\(\sin \left( {2018a} \right) = 2\sin \left( {1009a} \right).\cos \left( {1009a} \right).\)
Khẳng định nào sai trong các khẳng định sau?
\({\sin ^2}x = \frac{{1 - \cos 2x}}{2}.\)
\({\cos ^2}x = \frac{{1 + \cos 2x}}{2}.\)
\(\sin x = 2\sin \frac{x}{2}\cos \frac{x}{2}.\)
\(\cos 3x = {\cos ^3}x - {\sin ^3}x.\)
Công thức nào sau đây đúng?
\[\cos 3a = 3\cos a - 4{\cos ^3}a.\]
\[\cos 3a = 4{\cos ^3}a - 3\cos a.\]
\[\cos 3a = 3{\cos ^3}a - 4\cos a.\]
\[\cos 3a = 4\cos a - 3{\cos ^3}a.\]
Cho \(0 < \alpha ,{\rm{ }}\beta < \frac{\pi }{2}\) và thỏa mãn \(\tan \alpha = \frac{1}{7}\), \(\tan \beta = \frac{3}{4}\). Góc có giá trị bằng
\(\frac{\pi }{3}.\)
\(\frac{\pi }{4}.\)
\(\frac{\pi }{6}.\)
\(\frac{\pi }{2}.\)
Nếu \(\tan \left( {a + b} \right) = 7,\,\,\,\tan \left( {a - b} \right) = 4\) thì giá trị đúng của \(\tan 2a\) là
\( - \frac{{11}}{{27}}.\)
\(\frac{{11}}{{27}}.\)
\( - \frac{{13}}{{27}}.\)
\(\frac{{13}}{{27}}.\)
Rút gọn biểu thức \(M = \tan x - \tan y\).
\(M = \tan \left( {x - y} \right).\)
\(M = \frac{{\sin \left( {x + y} \right)}}{{\cos x.\cos y}}.\)
\(M = \frac{{\sin \left( {x - y} \right)}}{{\cos x.\cos y}}.\)
\(M = \frac{{\tan x - \tan y}}{{1 + \tan x.\tan y}}.\)
Giá trị của biểu thức \[P = \frac{{\sin \frac{{5\pi }}{{18}}\cos \frac{\pi }{9} - \sin \frac{\pi }{9}\cos \frac{{5\pi }}{{18}}}}{{\cos \frac{\pi }{4}\cos \frac{\pi }{{12}} - \sin \frac{\pi }{4}\sin \frac{\pi }{{12}}}}\] là
\(1\).
\[\frac{1}{2}.\]
\[\frac{{\sqrt 2 }}{2}.\]
\[\frac{{\sqrt 3 }}{2}.\]
Trong \[\Delta ABC\], nếu \[\frac{{\sin B}}{{\sin C}} = 2\cos A\] thì \[\Delta ABC\] là tam giác có tính chất nào sau đây?
Cân tại \(B.\)
Cân tại \(A.\)
Cân tại \(C.\)
Vuông tại \(B.\)
Cho góc \[\alpha \] thỏa mãn \[\frac{\pi }{2} < \alpha < \pi \] và \[\sin \alpha = \frac{4}{5}\]. Tính \[P = \sin 2\left( {\alpha + \pi } \right).\]
\(P = - \frac{{24}}{{25}}.\)
\(P = \frac{{24}}{{25}}.\)
\(P = - \frac{{12}}{{25}}.\)
\(P = \frac{{12}}{{25}}.\)
Cho \[x,{\rm{ }}y\] là các góc nhọn và dương thỏa mãn \[\cot x = \frac{3}{4},\,\,\,\cot y = \frac{1}{7}.\] Tổng \[x + y\] bằng
\(\frac{\pi }{4}.\)
\(\frac{{3\pi }}{4}.\)
\(\frac{\pi }{3}.\)
\[\pi .\]
Nếu \(\tan \alpha \) và \(\tan \beta \) là hai nghiệm của phương trình \[{x^2} + px + q = 0{\rm{ }}\left( {q \ne 1} \right)\] thì \(\tan \left( {\alpha + \beta } \right)\) bằng
\[\frac{p}{{q - 1}}.\]
\[ - \frac{p}{{q - 1}}.\]
\[\frac{{2p}}{{1 - q}}.\]
\[ - \frac{{2p}}{{1 - q}}.\]
Nếu \(\alpha + \beta + \gamma = \frac{\pi }{2}\) và \(\cot \alpha + \cot \gamma = 2\cot \beta \) thì \(\cot \alpha .\cot \gamma \) bằng
\(\sqrt 3 .\)
\( - \,\sqrt 3 .\)
\(3.\)
\( - \,3.\)
Biết \(\sin a = \frac{8}{{17}},\tan b = \frac{5}{{12}}\) và \(a\), \(b\) là các góc nhọn.
a) \(\tan a = \frac{8}{{15}}\).
b) \(\sin \left( {a - b} \right) = \frac{{21}}{{221}}\).
c) \(\cos \left( {a + b} \right) = \frac{{14}}{{22}}\).
d) \(\tan \left( {a + b} \right) = \frac{{17}}{{14}}.\)
Biết \(\tan \alpha = 2\).
a) \(\cot \alpha = - \frac{1}{2}\).
b) \(\cos 2\alpha = - \frac{3}{5}\).
c) \(\sin 2\alpha = \frac{4}{5}\).
d) \(\tan 2\alpha = - \frac{4}{3}\).
Biết \(\sin 2\alpha = - \frac{4}{5},\frac{\pi }{2} < \alpha < \frac{{3\pi }}{2}\).
a) \(\cos \alpha < 0\).
b) \(2\sin \alpha \cos \alpha = - \frac{4}{5}\).
c) \(\cos \alpha = \frac{{ - 2}}{{\sqrt 5 }},\sin \alpha = \frac{1}{{\sqrt 5 }}\).
d) \(\cos \alpha = \frac{{ - 1}}{{\sqrt 5 }},\sin \alpha = - \frac{2}{{\sqrt 5 }}\).
Biết \(\cos 2\alpha = \frac{5}{9},0^\circ < \alpha < 90^\circ \).
a) \(\sin \alpha = \frac{{\sqrt {28} }}{9}\).
b) \(\cos \alpha = \frac{{\sqrt {53} }}{9}\).
c) \(\tan \alpha = \frac{{\sqrt {371} }}{{53}}\).
d) \(\cot \alpha = \frac{{\sqrt {371} }}{{14}}\).
Cho \(\cos x = \frac{1}{5},\frac{\pi }{2} < x < \pi \).
a) \[\sin \frac{x}{2} = \frac{{\sqrt {10} }}{4}\].
b) \(\cos \frac{x}{2} = \frac{{\sqrt {15} }}{4}\).
c) \(\tan \frac{x}{2} = \frac{{\sqrt 6 }}{3}\).
d) \(\cot \frac{x}{2} = \frac{{\sqrt 6 }}{2}\).
PHẦN III. TRẢ LỜI NGẮN
Cho các góc \(\alpha ,\beta \) thỏa mãn \(\frac{\pi }{2} < \alpha ,\beta < \pi ,\sin \alpha = \frac{1}{3},\cos \beta = - \frac{2}{3}\).
Biết \(\sin \left( {\alpha + \beta } \right) = - \frac{{a\left( {1 + \sqrt {10} } \right)}}{b}\) với \(\frac{a}{b}\) là phân số tối giản và \(b > 0\). Tính \(a + b\).
Cho hai góc nhọn \(a\) và \(b\) với \(\tan a = \frac{1}{7}\) và \(\tan b = \frac{3}{4}\). Biết \(a + b = n^\circ \). Giá trị \(n\) bằng bao nhiêu?
Biến đổi thành tổng biểu thức \(P = 4\sin 3x\sin 2x\cos x\) ta được
\(P = a\cos 2x + b\cos 4x + c\cos 6x + d\).
Tính \(a + b + c + d\).
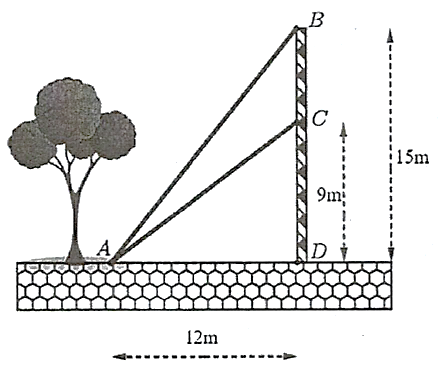
Từ một vị trí \(A\), người ta buộc hai sợi cáp \(AB\) và \(AC\) đến một cái trụ cao \(15\;\,{\rm{m}}\), được dựng vuông góc với mặt đất, chân trụ ở vị trí \(D\). Biết \(CD = 9{\rm{\;m}}\) và \(AD = 12\;\,{\rm{m}}\). Số đo góc nhọn \(\alpha = \widehat {BAC}\) tạo bởi hai sợi dây cáp đó bằng bao nhiêu độ (làm tròn kết quả đến hàng phần mười)?
Cho \[\cot \alpha = - 3\sqrt 2 \] với \[\frac{\pi }{2} < \alpha < \pi \]. Khi đó giá trị \[\tan \frac{\alpha }{2} + \cot \frac{\alpha }{2}\] bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?








