Đề kiểm tra Công thức lượng giác (có lời giải) - Đề 1
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
Tính \[\sin {105^0}\] ta được:
\[\frac{{\sqrt 6 - \sqrt 2 }}{4}\].
\[ - \frac{{\sqrt 6 - \sqrt 2 }}{4}\].
\[\frac{{\sqrt 6 + \sqrt 2 }}{4}\].
\[ - \frac{{\sqrt 6 + \sqrt 2 }}{4}\].
Tính \[\tan {105^0}\] ta được:
\[ - (2 + \sqrt 3 )\].
\[2 + \sqrt 3 \].
\[2 - \sqrt 3 \].
\[ - (2 - \sqrt 3 )\].
Rút gọn biểu thức: \[\cos {54^0}\cos {4^0} - \cos {36^0}\cos {86^0}\], ta được:
\[\cos {50^0}\].
\[\cos {58^0}\].
\[\sin {50^0}\].
\[\sin {58^0}\].
Giá trị của biểu thức \[\cos \frac{{37\pi }}{{12}}\] bằng
\[\frac{{\sqrt 6 + \sqrt 2 }}{4}.\]
\[\frac{{\sqrt 6 - \sqrt 2 }}{4}.\]
–\[\frac{{\sqrt 6 + \sqrt 2 }}{4}.\]
\[\frac{{\sqrt 2 - \sqrt 6 }}{4}.\]
Khẳng định nào dưới đây SAI?
\(2{\sin ^2}a = 1 - \cos 2a\).
\(\cos 2a = 2\cos a - 1\).
\(\sin 2a = 2\sin a\cos a\).
\(\sin \left( {a + b} \right) = \sin a\cos b + \sin b.\cos a\).
Cho hai góc nhọn \(a\) và \(b\). Biết \[\cos a = \frac{1}{3}\], \[\cos b = \frac{1}{4}\]. Giá trị \[\cos \left( {a + b} \right).\cos \left( {a - b} \right)\] bằng
\[ - \frac{{113}}{{144}}.\]
\[ - \frac{{115}}{{144}}.\]
\[ - \frac{{117}}{{144}}.\]
\[ - \frac{{119}}{{144}}.\]
Nếu biết \(\sin a = \frac{8}{{17}},\,\tan b = \frac{5}{{12}}\) và \(a,\,b\) đều là các góc nhọn và dương thì \(\sin \left( {a - b} \right)\) là:
\(\frac{{20}}{{220}}\).
\( - \frac{{20}}{{220}}\).
\(\frac{{21}}{{221}}\).
\(\frac{{22}}{{221}}\).
Nếu \(\tan x = 0.5;\,\,\sin y = \frac{3}{5}\,\,\left( {0 < y < {{90}^0}} \right)\) thì \(\tan \left( {x + y} \right)\) bằng:
\[2\].
\(3\).
\(4\).
\(5\).
Biểu thức \[\frac{{3 - 4\cos 2\alpha + cos4\alpha }}{{3 + 4\cos 2\alpha + cos4\alpha }}\] có kết quả rút gọn bằng:
\[ - {\tan ^4}\alpha \].
\[{\tan ^4}\alpha \].
\[ - {\cot ^4}\alpha \].
\[{\cot ^4}\alpha \].
Nếu \(\tan \frac{x}{2} = \frac{1}{2}\) thì giá trị của biểu thức \(\frac{{\sin x}}{{2 - 3\cos x}}\) bằng.
\(1\).
\[2\].
\(3\).
\[4\].
Tích số \[\cos 10^\circ .\cos 30^\circ .\cos 50^\circ .\cos 70^\circ \] bằng
\[\frac{1}{{16}}.\]
\[\frac{1}{8}.\]
\[\frac{3}{{16}}.\]
\[\frac{1}{4}.\]
Biết \[A,\,\,B,\,\,C\] là các góc của tam giác \[ABC,\] khi đó.
\[\sin C = - \sin \left( {A + B} \right).\]
\[\cos C = \cos \left( {A + B} \right).\]
\[\tan C = \tan \left( {A + B} \right).\]
\[\cot C = - \cot \left( {A + B} \right).\]
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho biết \(\cos 2\alpha = - \frac{1}{4}\) và \(\pi < \alpha < \frac{{3\pi }}{2}\). Khi đó:
a) \(\sin \alpha < 0,\cos \alpha < 0\)
b) \(\sin \alpha = \frac{{\sqrt {10} }}{4}\)
c) \(\cos \alpha = \frac{{\sqrt 6 }}{4}\)
d) \(\cot \alpha = \frac{{\sqrt {15} }}{5}\)
Biến đổi được các biểu thức sau về dạng tích số. Khi đó:
a) \(\cos 3x + \cos x = 2\cos 2x \cdot \cos 3x\)
b) \(\sin 3x + \sin 2x = 2\sin 2x\cos \frac{x}{2}\);
c) \(\cos 4x - \cos x = - 2\sin \frac{{5x}}{2}\sin \frac{{3x}}{2}\)
d) \(\sin 5x - \sin x = 2\cos 3x\sin 2x\)
Cho biết \(\sin \alpha = \frac{3}{5},\frac{\pi }{2} < \alpha < \pi \). Khi đó:
a) \(\cos \alpha < 0\)
b) \(\cos \alpha = - \frac{4}{5}\)
c) \(\tan \alpha = \frac{3}{4}\)
d) \(\tan \left( {\alpha + \frac{\pi }{3}} \right) = \frac{{48 - \sqrt 3 }}{{11}}\)
Cho \(\cos x = \frac{1}{5},\frac{\pi }{2} < x < \pi \). Khi đó:
a) \[\sin \frac{x}{2} = \frac{{\sqrt {10} }}{4}\]
b) \(\cos \frac{x}{2} = \frac{{\sqrt {15} }}{4}\)
c) \(\tan \frac{x}{2} = \frac{{\sqrt 6 }}{3}\)
d) \(\cot \frac{x}{2} = \frac{{\sqrt 6 }}{2}\)
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Cho \(\sin x = \frac{1}{5},\frac{\pi }{2} < x < \pi \). Tính \(\cot 2x\).
Cho các góc \(\alpha ,\beta \) thỏa mãn \(\frac{\pi }{2} < \alpha ,\beta < \pi ,\sin \alpha = \frac{1}{3},\cos \beta = - \frac{2}{3}\).
Tính \(\sin (\alpha + \beta )\).
Rút gọn \(C = \tan 3x - \tan x - \frac{{2\sin x}}{{\cos 3x}}\)
Có hai chung cư cao tầng xây cạnh nhau với khoảng cách giữa chúng là HK = 20 m. Để đảm bảo an ninh, trên nóc chung cư thứ hai người ta lắp camera ở vị trí C. Gọi A, B lần lượt là vị trí thấp nhất, cao nhất trên chung cư thứ nhất mà camera có thể quan sát được (Hình 18). Hãy tính số đo góc ACB (phạm vi camera có thể quan sát được ở chung cư thứ nhất). Biết rằng chiều cao của chung cư thứ hai là CK = 32 m, AH = 6 m, BH = 24 m (làm tròn kết quả đến hàng phần mười theo đơn vị độ).
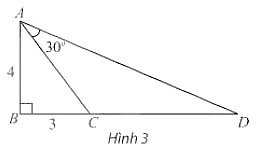
Trong Hình 3, tam giác ABC vuông tại \(B\) và có hai cạnh góc vuông là AB = 4,BC = 3. Vẽ điểm \(D\) nằm trên tia đối của tia \(CB\) thoả mãn \(\widehat {CAD} = {30^ \circ }\). Tính \({\rm{tan}}\widehat {{\rm{ }}BAD}\), từ đó tính độ dài cạnh \(CD\).
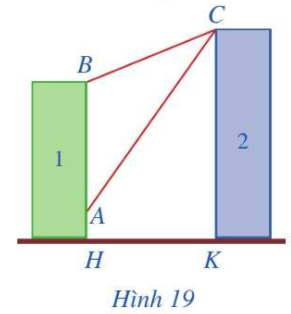
Trong Hình 4, pit-tông \(M\)của động cơ chuyển động tịnh tiến qua lại dọc theo xi-lanh làm quay trục khuỷu \(IA\). Ban đầu \(I,A,M\) thẳng hàng. Cho \(\alpha \)là góc quay của trục khuỷu, \(O\) là vị trí của pít-tông khi \(\alpha = \frac{\pi }{2}\) và là hình chiếu của \(A\) lên \(Ix\). Trục khuỷu \(IA\) rất ngắn so với độ dài thanh truyền \(AM\) nên có thể xem như độ dài \(MH\)không đổi và gần bằng \(MA\).
a) Biết \(LA = 8{\rm{\;cm}}\), viết công thức tính toạ độ \({x_M}\) của điểm \(M\) trên trục \(Ox\) theo \(\alpha \).
b) Ban đầu \(\alpha = 0\). Sau 1 phút chuyền động, \({x_M} = - 3{\rm{\;cm}}\). Xác định \({x_M}\) sau 2 phủt chuyển động. Làm tròn kết quả đến hàng phần mười.