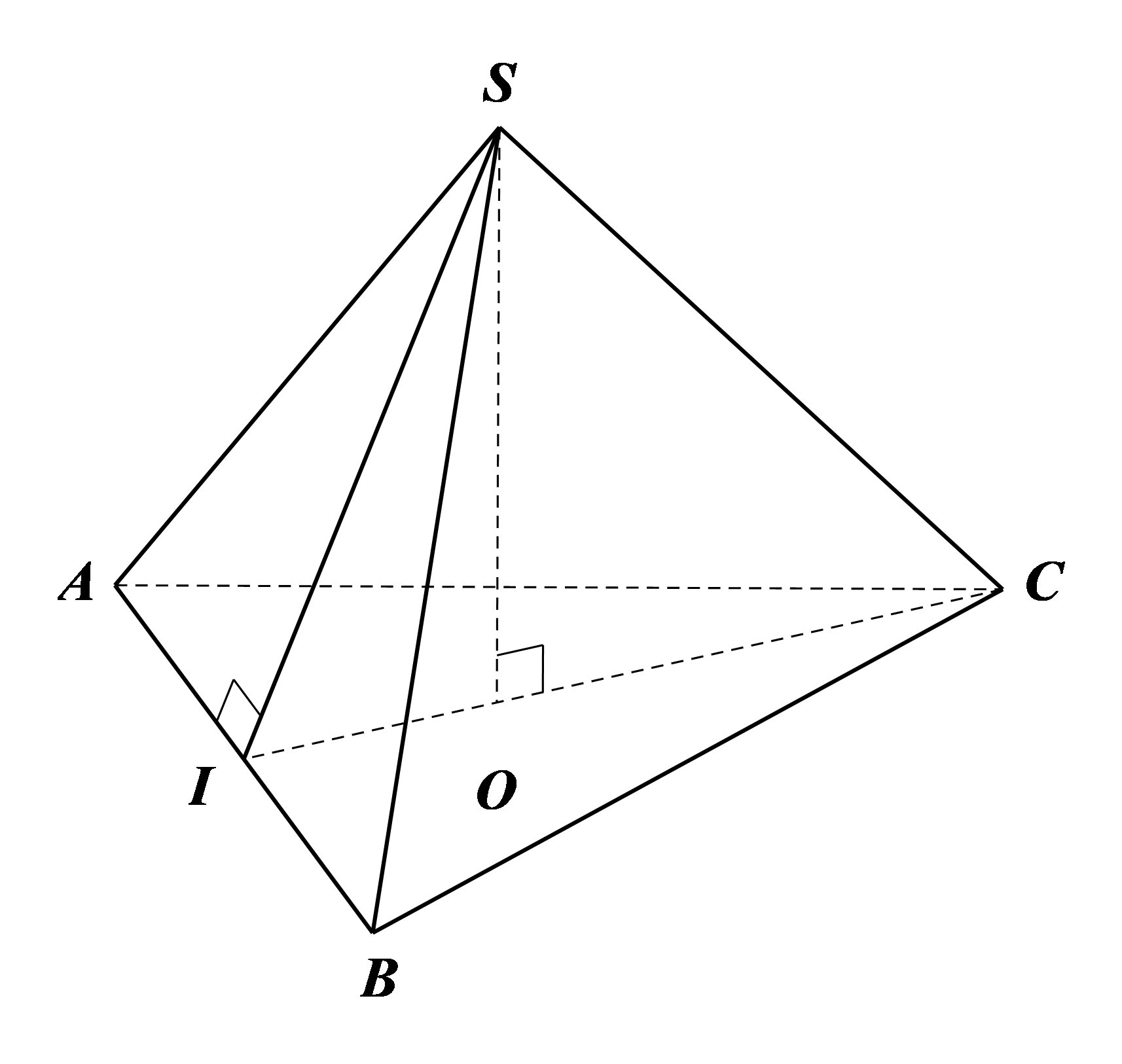Đề cương ôn tập giữa kì 1 Toán 8 Cánh diều cấu trúc mới (Tự luận) có đáp án - Phần 2

Một người làm vườn có hai khu vườn, khu vườn hình chữ nhật có chiều dài \(\left( {x + 2} \right)\,\,{\rm{m}}\,{\rm{,}}\) chiều rộng \(\left( {x - 1} \right)\,\,{\rm{m}}\,{\rm{,}}\) khu vườn hình vuông cạnh là \(\left( {x + 1} \right)\,\,{\rm{m}}\,{\rm{.}}\) Viết biểu thức đại số tính tổng diện tích của hai khu vườn trên.

Thầy Việt dự định mua \[x\] quyển vở để trao thưởng cho những học sinh tiến bộ cuối năm học, mỗi quyển vở giá \[y\] đồng. Nhưng khi đến cửa hàng thầy Việt thấy giá vở đã giảm 2000 đồng mỗi quyển nên quyết định mua thêm 30 quyển.

a) Tìm đa thức biểu thị số tiền thầy Việt phải trả cho cửa hàng.

b) Hãy cho biết bậc của đa thức vừa tìm được ở câu a và tính số tiền thầy Việt phải trả nếu thầy mua 50 quyển vở và giá 1 quyển vở khi chưa giảm là 7000 đồng.

Khu vườn của nhà bác Hoa có dạng hình vuông. Bác Hoa muốn dành một mảnh đất có dạng hình chữ nhật ở góc khu vườn làm nhà để dụng cụ làm vườn (hình vẽ).

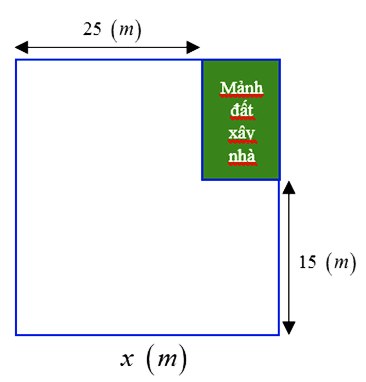
a) Viết đa thức biểu thị chu vi của mảnh đất làm nhà.

b) Biết chu vi của mảnh đất dành để làm nhà bằng \[40\,\,{\rm{m}}\]. Tính diện tích của khu vườn hình vuông ban đầu.

Một sân vận động hình chữ nhật có chiều dài \(5x + 3y\,\,(m)\) và chiều rộng \(5x - 3y\,\,(m).\) Mỗi cạnh được chừa ra 3 m làm lối đi, phần trong là phần sân trồng cỏ phục vụ cho các trận bóng đá. Tính diện tích mặt sân có trồng cỏ theo \(x\) và \(y.\) Tính số tiền trồng cỏ cho mặt sân trên khi \(x = 10\,;\,\,y = 2.\) Biết số tiền để trồng \(1\,\,{{\rm{m}}^{\rm{2}}}\) cỏ là \(50\,\,000\) đồng.

Cho biểu thức \[A = \frac{{{x^3} - 1}}{{{x^2} - 4}} \cdot \left( {\frac{1}{{x - 1}} - \frac{{x + 1}}{{{x^2} + x + 1}}} \right).\]

a) Tìm điều kiện xác định của biểu thức \(A.\)

b) Rút gọn biểu thức \(A.\)

c) Tính giá trị của biểu thức \(A\) biết \(\left| {x + 3} \right| = 1.\)

Cho biểu thức \(P = \left( {\frac{{5x + 2}}{{x - 10}} + \frac{{5x - 2}}{{x + 10}}} \right) \cdot \frac{{x - 10}}{{{x^2} + 4}}.\)

a) Tìm điều kiện xác định của \[P.\]

b) Rút gọn biểu thức \[P.\]

c) Tính giá trị của \[P\]khi\[x = \frac{2}{5}.\]

Cho biểu thức \(P = \left( {\frac{{x - 1}}{{{x^2} - 2x}} + \frac{{x + 1}}{{{x^2} + 2x}} - \frac{4}{{{x^3} - 4x}}} \right):\left( {1 - \frac{2}{x}} \right).\)

a) Tìm điều kiện xác định của biểu thức \[P\].

b) Rút gọn biểu thức \[P\].

c) Tính giá trị của biểu thức \[P\] biết \[x\] là số thực thỏa mãn điều kiện \[\left| {2x - 1} \right| = 5\].

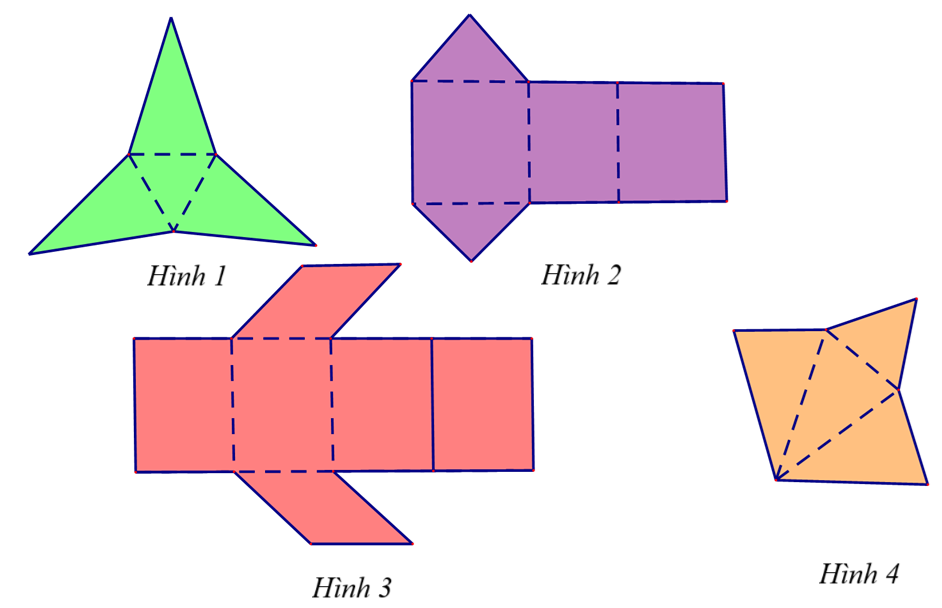
Trong các miếng bìa ở hình 1; hình 2; hình 3; hình 4; miếng bìa nào có thể gấp lại (theo các nét đứt) để được hình chóp tam giác đều?

Hình ảnh bên là khối rubik có bốn mặt , các mặt bên, mặt đáy là các tam giác đều.

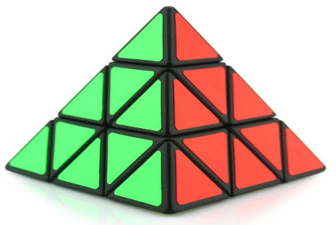
a) Khối rubik có dạng như hình bên thường được gọi là hình gì?

b) Cho biết số mặt, số cạnh, số đỉnh của hình khối bên ?

c) Hình vẽ bên là hình ảnh một chiếc rubik – 4 mặt , mỗi mặt đều được ghép bởi những tam giác đều nhỏ bằng nhau. Hãy cho biết có bao nhiêu tam giác đều có trên một mặt của chiếc rubik này?

Cho hình hộp chữ nhật có các kích thước như hình vẽ.

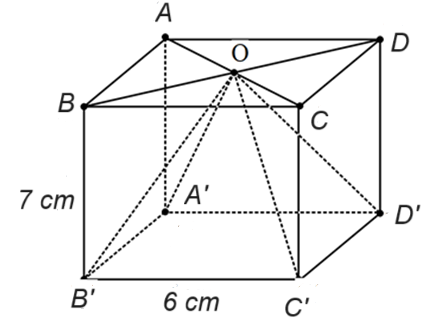
 Tính thể tích hình chóp tam giác đều\(O.A'B'C'D'\).

Bạn Hà làm một cái lòng đèn hình quả trám (như hình bên) là hình ghép từ hai hình chóp tứ giác đều có cạnh đáy \[20\,\,{\rm{cm}}\], cạnh bên \[32\,\,{\rm{cm}}\], khoảng cách giữa hai đỉnh của hai hình chóp là \[30\,\,{\rm{cm}}.\]

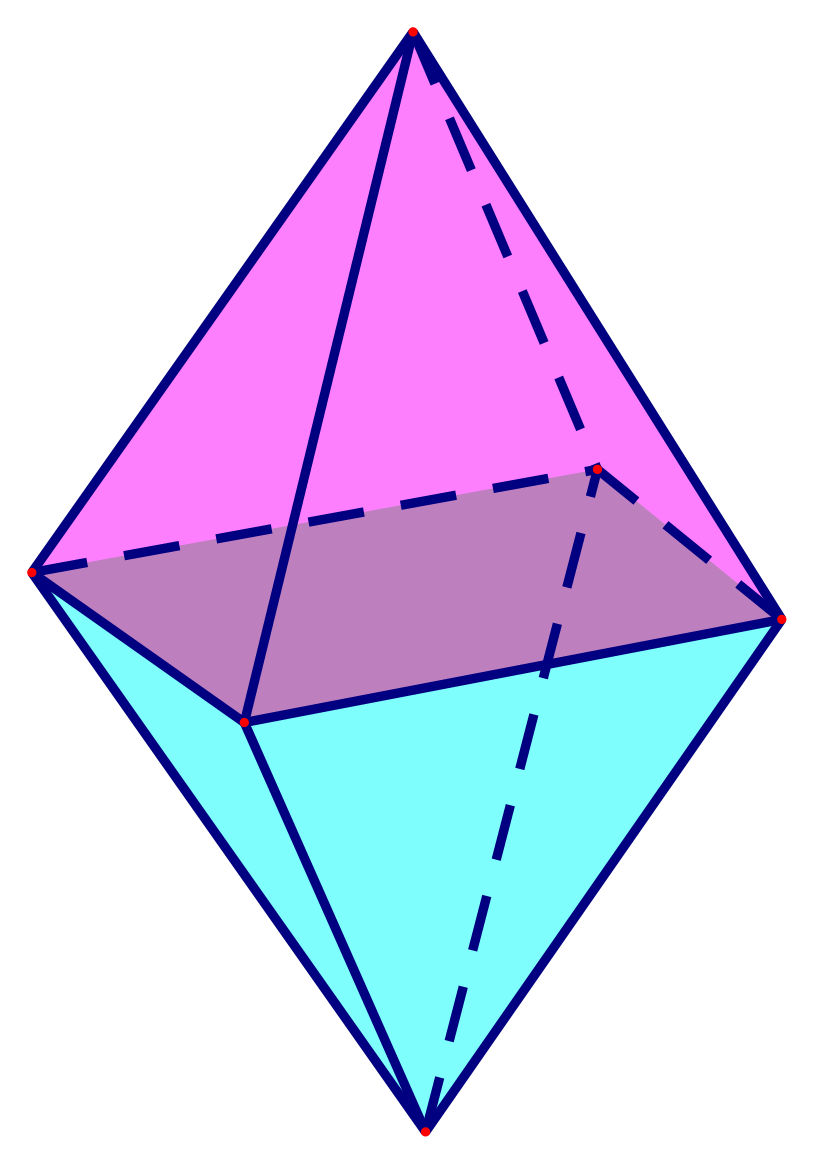
a) Tính thể tích của lòng đèn.

b) Bạn Hà muốn làm 50 cái lòng đèn hình quả trám này cần phải chuẩn bị bao nhiêu mét thanh tre? (mối nối giữa các que tre có độ dài không đáng kể).

a) Một chiếc đèn thả trần có dạng hình chóp tam giác đều có tất cả các cạnh đều khoảng \[20\,\,{\rm{cm}}.\] Độ dài trung đoạn khoảng \[17,32{\rm{ cm}}.\] Tính diện tích xung quanh của chiếc đèn thả trần đó.

b) Cho hình chóp tam giác đều \[S.ABC\] có cạnh đáy bằng \[4\,\,cm\] và chiều cao tam giác đáy là \[3,5\,\,{\rm{cm;}}\] trung đoạn bằng \[5\,\,{\rm{cm}}.\] Tính diện tích xung quanh và diện tích toàn phần (tức là tổng diện tích các mặt) của hình chóp.

Kim tự tháp Louvre là một công trình kiến trúc tuyệt đẹp bằng kính tọa lạc ngay lối vào của bảo tàng Louvre, Pari. Kim tự tháp có dạng là hình chóp tứ giác đều với chiều cao 21 m và độ dài cạnh đáy là 34 m. Các mặt bên của kim tự tháp là các tam giác đều (hình ảnh minh họa).

a) Tính thể tích của kim tự tháp Louvre.

b) Tổng diện tích thật sự của sàn kim tự tháp là \(1\,\,000\,\,{{\rm{m}}^{\rm{2}}}\). Hỏi nếu sử dụng loại gạch hình vuông có cạnh là \[60\,\,{\rm{cm}}\] để lót sàn thì cần bao nhiêu viên gạch?

c) Mỗi mặt của Kim tự tháp (trừ mặt có cổng ra vào) được tạo thành từ 18 tấm kính hình tam giác đều và 17 hàng kính hình thoi xếp chồng lên nhau. Hỏi có bao nhiêu tấm kính hình thoi trên mỗi mặt?

Một khối bê tông có dạng như hình dưới đây. Phần dưới của khối bê tông có dạng hình hộp chữ nhật, đáy là hình vuông có cạnh \(4{\rm{ dm,}}\) chiều cao \({\rm{2,5 dm}}{\rm{.}}\) Phần trên của khối bê tông có dạng hình chóp tứ giác đều, chiều cao \({\rm{10 dm}}{\rm{.}}\)

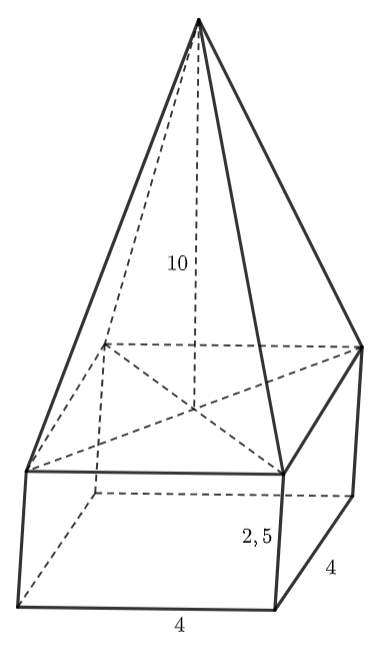
Tính thể tích của khối bê tông đó.

Một chiếc lều ở trại hè cho học sinh có dạng hình chóp tứ giác đều với chiều cao bằng \[2,8\,\,{\rm{m}};\] độ dài cạnh đáy bằng \[3\,{\rm{m}}\,{\rm{.}}\]

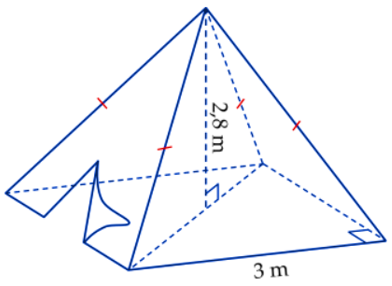
a) Tính thể tích không khí bên trong của chiếc lều.

b) Người ta muốn sơn phủ bên ngoài cả bốn mặt xung quanh của lều và không sơn phủ phần làm cửa có diện tích là \[5\,\,{{\rm{m}}^2}.\] Biết độ dài trung đoạn của lều là \[3,18\,\,{\rm{m}}\]và cứ mỗi mét vuông sơn cần trả \[35\,\,000\] đồng. Tính số tiền cần phải trả để hoàn thành việc sơn phủ cho lều.

Một chiếc thang có chiều dài \[AB = 3,7\,\,{\rm{m}}\] đặt cách một bức tường khoảng cách \[BH = 1,2\,\,{\rm{m}}.\] Biết rằng khoảng cách “an toàn” khi \(2,0 < \frac{{AH}}{{BH}} < 2,2\) (xem hình vẽ). Tính chiều cao \[AH.\] Từ đó kiểm tra xem khoảng cách đặt thang cách chân tường là \[BH\] có “an toàn” không?

Một viên bi lăn từ vị trí \(A\) đến vị trí \(D\) theo đường gấp khúc \(ABCD\) hết 21 giây, biết rằng \(AB = 10{\rm{\;cm}},\) \(BC = 12{\rm{\;cm}},\) \(CD = 6{\rm{\;cm}}\) (hình vẽ bên). Hỏi nếu viên bi đó lăn theo đoạn thẳng \(AD\) thì hết bao nhiêu giây? Giả sử vận tốc của viên bi không thay đổi.

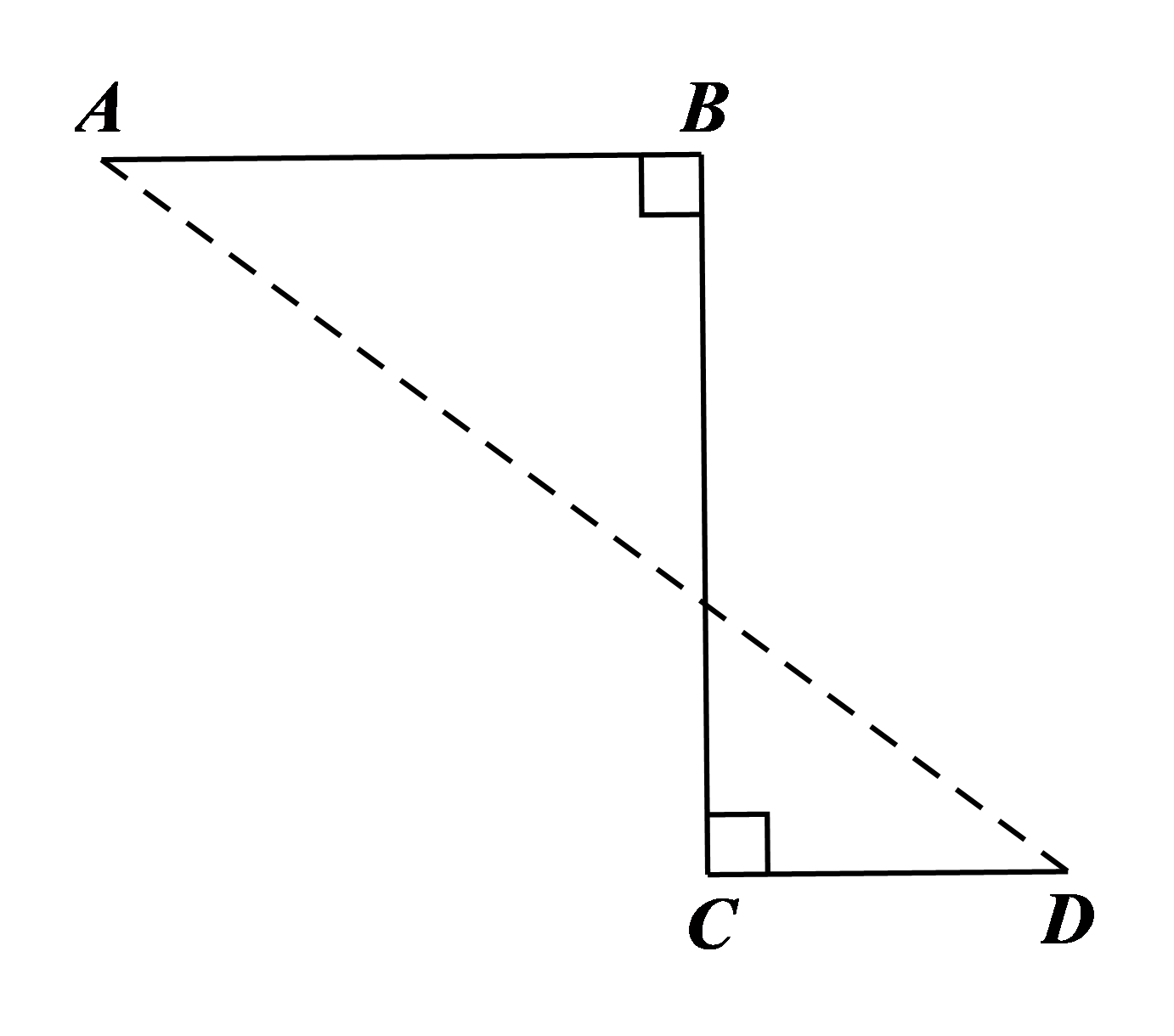
Khi xây móng nhà, để kiểm tra xem hai phần móng có vuông góc với nhau hay không, người thợ xây thường lấy \[AB = 3\,\,{\rm{cm}},{\rm{ }}AC = 4\,\,{\rm{cm}}\]\[(A\] là điểm chung của hai phần móng nhà hay còn gọi là góc nhà), rồi đo đoạn \[BC\] nếu \[BC = 5\,\,{\rm{cm}}\] thì hai phần móng đó vuông góc với nhau. Hãy giải thích vì sao?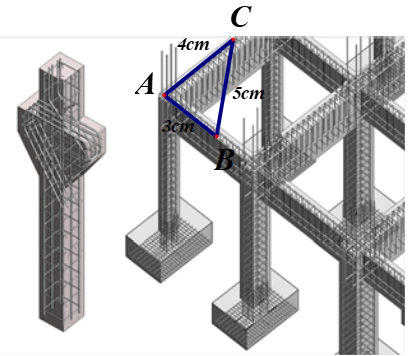

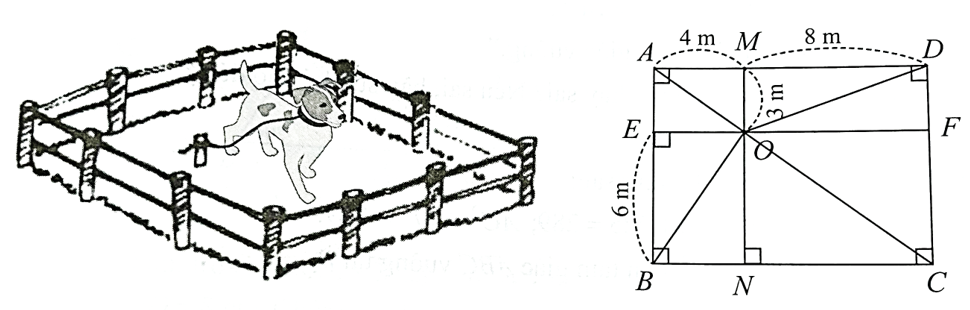
Người ta buộc chú cún bằng sợi dây có một đầu buộc cố định tại điểm \(O\) làm cho chú cún cách điểm \(O\) xa nhất là \(9{\rm{\;m}}.\) Hỏi với các kích thước đã cho như hình trên, chú cún có thể đến các vị trí \(A,\,\,B,\,\,C,\,\,D\) để canh giữ mảnh vườn hình chữ nhật \[ABCD\] hay không?

Chứng minh đẳng thức sau:

\(\left( {x + y} \right)\left( {{x^4} - {x^3}y + {x^2}{y^2} - x{y^3} + {y^4}} \right) = {x^5} + {y^5}\).

Cho các số \(x,y\) thỏa mãn đẳng thức: \(5{x^2} + 5{y^2} + 8xy - 2x + 2y + 2 = 0.\) Tính giá trị của biểu thức \(M = {\left( {x + y} \right)^{2023}} + {\left( {x - 2} \right)^{2024}} + {\left( {y + 1} \right)^{2025}}\).

Tính giá trị của biểu thức: \(A = 4\left( {{3^2} + 1} \right)\left( {{3^4} + 1} \right)\left( {{3^8} + 1} \right)\,\,...\,\,\left( {{3^{64}} + 1} \right)\).

Chứng minh rằng nếu \[{a^4} + {b^4} + {c^4} + {d^4} = 4abcd\] và\(a,\,\,b,\,\,c,\,\,d\) là các số dương thì \[a = b = c = d.\]

Tìm \(m,\,\,n \in \mathbb{N}\) để phép chia sau đây là phép chia hết:

\(\left( {4{x^6}{y^7} - 10{x^5}{y^6} + 8{x^4}{y^5}} \right):\left( { - 4{x^m}{y^n}} \right)\).

Cho các số x, y thoả mãn \({x^2} + {y^2} - 3x - 3y + xy + 3 = 0\). Tính giá trị của biểu thức \(Q = {\left( {x - y} \right)^{2023}} + {\left( {x - 2} \right)^{2024}} + {y^{2025}}\).

Tìm giá trị nhỏ nhất củabiểu thức \[M = 9{x^2} + 6{y^2} + 18x - 12xy - 12y - 27\].

Cho các số thực \(a,\,\,b,\,\,c\) thoả mãn \({a^2} + {b^2} + {c^2} = 3\) và \(a + b + c + ab + bc + ca = 6.\) Tính giá trị của biểu thức \[A = \frac{{{a^9} + {b^{11}} + {c^{2025}}}}{{{a^{2023}} + {b^{2024}} + {c^{2025}}}}.\]

a) Tìm giá trị lớn nhất của phân thức \(A = \frac{{35}}{{{x^2} - 2x + 6}}\).

b) Tìm giá trị nhỏ nhất của phân thức \[B = \frac{{12}}{{12 - 4x - {x^2}}}\].

Tìm \(a,\,\,b,\,\,c \in \mathbb{N}*\) sao cho \(\left( {a - \frac{1}{b}} \right)\left( {b - \frac{1}{c}} \right)\left( {c - \frac{1}{a}} \right) \in \mathbb{N}*\).

Cho \(\frac{a}{{b + c}} + \frac{b}{{c + a}} + \frac{c}{{a + b}} = 1.\) Chứng minh rằng \(\frac{{{a^2}}}{{b + c}} + \frac{{{b^2}}}{{c + a}} + \frac{{{c^2}}}{{a + b}} = 0.\)

Ao Bà Om, hay Ao Vuông là một thắng cảnh độc đáo và nổi tiếng ở tỉnh Vĩnh Long (trước đây là tỉnh Trà Vinh), Việt Nam. Mặt ao nước trong xanh và phẳng lặng được phủ bởi hoa sen, hoa súng. Ao được bao bọc xung quanh bởi các gò cát mấp mô với các hàng cây sao, cây dầu cổ thụ hàng trăm năm tuổi có rễ nổi lên khỏi mặt đất tạo nên những hình thù kì lạ. Ao có hình chữ nhật, rộng \[x\] mét, dài \(\left( {x + 200} \right)\) mét, được đào ở trung tâm miếng đất hình vuông có cạnh là \(\left( {x + 400} \right)\) mét. Hãy tính diện tích phần đất còn lại sau khi đào ao.

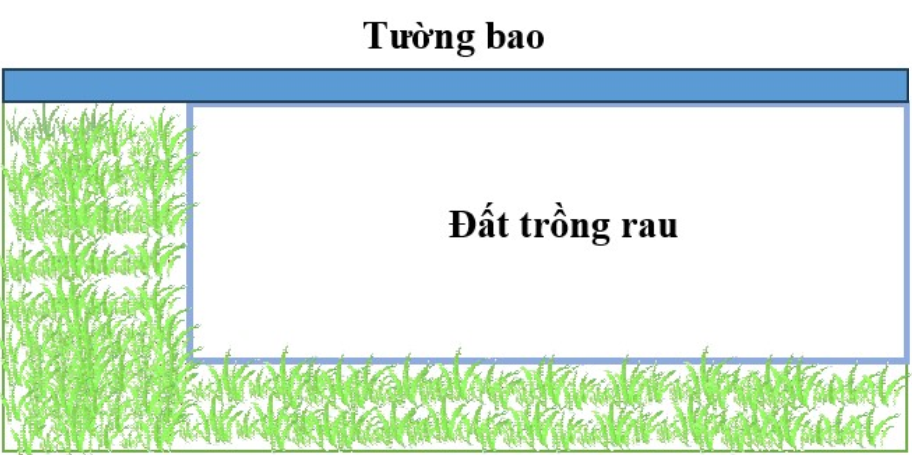
Gia đình bác Nam có một khu đất hình chữ nhật, một cạnh đã được xây tường bao (như hình vẽ). Trên khu đất này, bác Nam định cải tạo một phần đất để trồng rau có dạng hình chữ nhật. Tận dụng tường bao đã có và \(40\,\,{\rm{m}}\) lưới B40, bác muốn vây ba mặt còn lại của phần đất trồng rau. Hỏi bác có thể vây kín được phần đất trồng rau có diện tích lớn nhất là bao nhiêu mét vuông?

Một công ty muốn xây dựng một đường ống dẫn dầu từ điểm \[A\] trên bờ biển đến một điểm \[C\] trên một hòn đảo như hình vẽ. Giá để xây dựng đường ống trên bờ là \[40\,\,000{\rm{ USD}}\] mỗi km và \[130\,\,000{\rm{ USD}}\] mỗi km để xây dưới nước. Hỏi công ty nên xây đường ống theo phương án nào để tiết kiệm chi phí nhất? Biết rằng công ty đưa ra ba phương án:

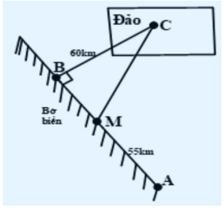
Phương án 1: Xây đường ống từ điểm \[A\] trên bờ đến điểm \[C\] trên đảo.Phương án 2: Xây đường ống từ điểm \[A\] đến điểm \(M\) trên bờ biển, rồi xây đường ống từ điểm \(M\) đến điểm \[C\] trên hòn đảo.Phương án 3: Xây đường ống từ điểm \[A\] đến điểm \(B\) trên bờ biển, rồi xây đường ống từ điểm \(B\) đến điểm \[C\] trên hòn đảo. Biết \(BC = 60\,\;{\rm{km}},\,\,AB = 100\,\;{\rm{km}},\,\,AM = 55\;\,{\rm{km}}{\rm{.}}\)

Cho hình chóp tam giác đều \(S.ABC,\) có cạnh đáy \(AB = 5{\rm{\;cm}}\) và độ dài trung đoạn \(SI = 6{\rm{\;cm}}\) (hình vẽ bên). Tính diện tích xung quanh và diện tích toàn phần của hình chóp \(S.ABC.\)(làm tròn các kết quả đến chữ số thập phân thứ hai)