Đề cương ôn tập giữa kì 1 Toán 8 Cánh diều cấu trúc mới (Đúng sai - Trả lời ngắn) có đáp án

Cho hai đa thức \(P = {x^2} - 4xy + 9\) và \(Q = - 6xy - 4{y^2} + 9.\)

Đa thức \(A\) và \(M\) thỏa mãn $P-A=Q;M=\left(x-2y\right)A-x^3+5.$

 a) Với \(x = 1\,;\,\,y = - 1\) thì giá trị của biểu thức \(P\) bằng 10.

 b) Đa thức \(Q\) có bậc là 2.

 c) \[A = {x^2} + xy + 4{y^2}.\]

 d) Giá trị của biểu thức \(M\) không phụ thuộc vào biến \(x.\)

Cho hai đa thức \(A = {x^2} - 4xy - 4\) và \(B = 2{x^2} - 3xy + {y^2} - 4.\)

Đa thức \(M\) và \(P\) thỏa mãn $B=A+M;P=\left(x-3\right)M-y-\left(x+y\right)\left(xy-3y\right).$

 a) Hạng tử tự do của đa thức \(A\) là \( - 4\).

 b) Với \(x = 1\,;\,\,y = 0\) thì giá trị của biểu thức \(B\) bằng \( - 2.\)

 c) \(M = {x^2} + 7xy + {y^2}.\)

 d) Giá trị của biểu thức \(P\) không phụ thuộc vào biến \(y\).

Cho hai biểu thức \(A\) và \(B\) thỏa mãn \(45{x^6}{y^3}:A = 5x{y^2}\) và \(\left( {B + 7{x^4}{y^2}} \right):A = 3x{y^2} + 2xy\).

 a) Biểu thức \(A\) là đơn thức bậc 3.

 b) Với \(x = - 1\,;\,\,y = 2\) thì giá trị của biểu thức \(A\) bằng \( - 18.\)

 c) \(B = 27{x^4}{y^4} + 11{x^4}{y^2}\).

 d) Tích của hai biểu thức \(A\) và \(B\) là \(36{x^7}{y^5} + 20{x^7}{y^3}.\)

Cho đa thức \(A = 3{x^2}y - 2x{y^2} - 4xy + 1.\)

Đa thức \(B\) và \(M\) thỏa mãn $B-A=-2x^{3}y+7x^{2}y+3xy;A+M=3x^2{y}^2-5x^{2}y+8xy.$

 a) Với \[x = - 1\,;\,\,y = 1\] thì giá trị của biểu thức \(A\) bằng 9.

 b) Đa thức \(B\) sau khi thu gọn có 5 hạng tử.

 c) Đa thức \(M\) có bậc là 2.

 d) Tổng của hai đa thức \(B\) và \(M\) có hạng tử tự do là 1.

Cho hai đa thức:

\(A = {x^2}y + 5xy - 1\) và \(B = 3y\left( {3y - x} \right) + \left( { - 2{x^2}{y^2} - 6x{y^3} + 4xy} \right):\frac{2}{3}xy\).

 a)Đa thức \(A\)có bậc là 2.

 b) Đa thức \(B\)không chia hết cho 6.

 c) Với \(x = \frac{1}{2};\) \(y = 4\) thì \(B = - 6\).

 d) Tổng của hai đa thức \(A\) và \(B\) có hạng tử tự do là 6.

Cho biểu thức \[K = \left( {\frac{{x + 1}}{{x - 1}} - \frac{{x - 1}}{{x + 1}} + \frac{{{x^2} - 4x - 1}}{{{x^2} - 1}}} \right) \cdot \frac{{x + 3}}{x}\].

 a) Điều kiện xác định của biểu thức \(K\) là \[x \ne 1\,;\,\,x \ne - \,1;\,\,x \ne 0\,;\,\,x \ne - \,3.\]

 b) Biểu thức \(K\) sau khi rút gọn là phân thức có tử thức là \(x + 3.\)

 c) Với \(x = - 1\) thì \(K = 2.\)

 d) Có 2 giá trị của \(x\) để biểu thức \(K\) nhận giá trị nguyên.

Cho biểu thức \[P = \frac{{{x^2} - 6x + 9}}{{9 - {x^2}}} + \frac{{4x + 8}}{{x + 3}}.\]

 a) Điều kiện xác định của biểu thức \(P\) là \[x \ne 3,\,\,x \ne - 3\].

 b) Biểu thức \(P\) sau khi rút gọn là phân thức có mẫu thức là \(9 - x.\)

 c) Biểu thức \(P\) có giá trị bằng 4 tại \(x = - 1\).

 d) Với \(\left| {x + 2} \right| = 1\) thì có 2 giá trị của biểu thức \(P\) .

Một bể kính hình hộp chữ nhật có hai cạnh đáy là \(60{\rm{ cm}}\) và \(30{\rm{ cm}}{\rm{.}}\) Trong bể có một khối đá hình chóp tam giác đều với diện tích đáy là \(270{\rm{ c}}{{\rm{m}}^2}\), chiều cao \(30{\rm{ cm}}{\rm{.}}\) Người ta đổ nước vào bể sao cho nước ngập khối đá và đo được mức nước là \(60{\rm{ cm}}{\rm{.}}\)

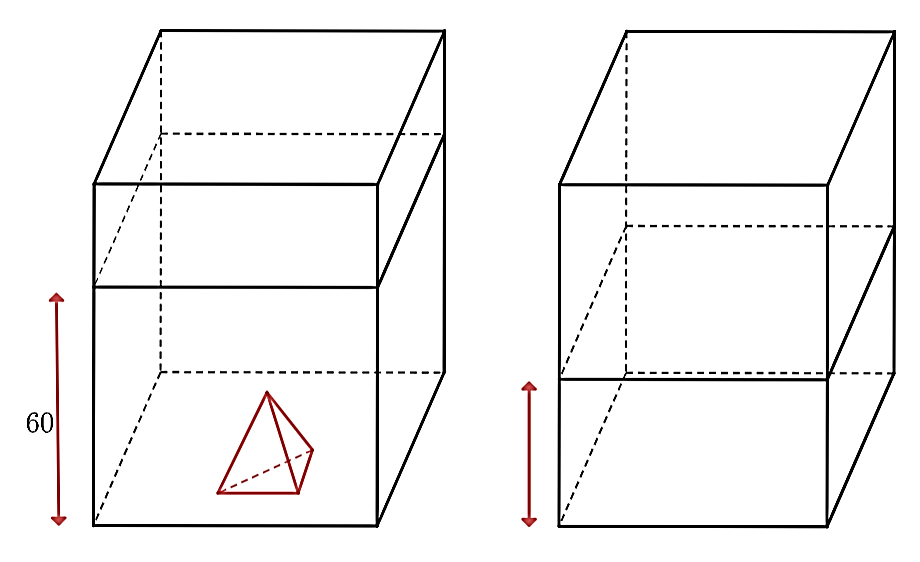
 a) Diện tích đáy của bể hình hộp chữ nhật là \(180{\rm{ c}}{{\rm{m}}^{\rm{2}}}\).

 b) Thể tích khối đá hình chóp tam giác đều là: \(2{\rm{ }}700{\rm{ c}}{{\rm{m}}^3}.\)

 c) Thể tích khối nước là\(108{\rm{ }}000{\rm{ c}}{{\rm{m}}^2}\).

 d) Khi lấy khối đá ra thì mực nước của bể cao 56 cm.

Đỉnh Fansipan (Lào Cai) cao \(3143{\rm{ m,}}\) là đỉnh núi cao nhất Đông Dương. Trên đỉnh núi, người ta đặt một chóp làm bằng inox có dạng hình chóp tam giác đều dài \(60{\rm{ cm,}}\)chiều cao \(90{\rm{ cm}}\) (như hình vẽ).

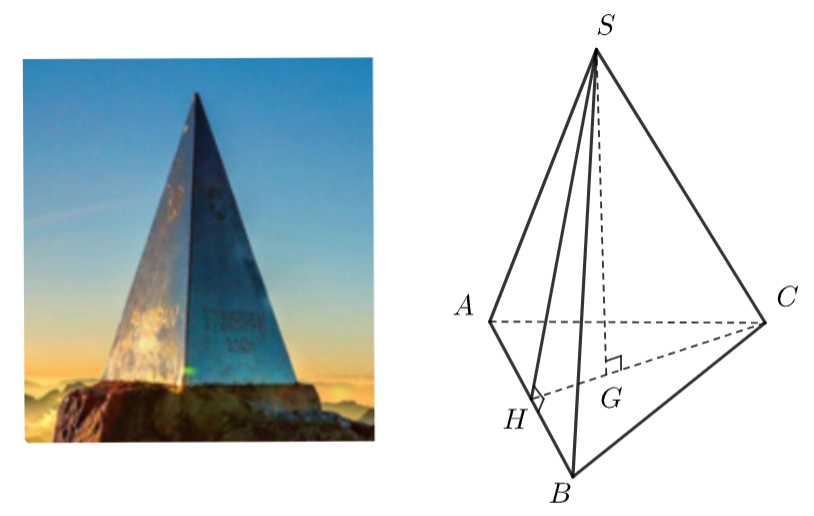
 a) Tam giác đều \(ABC\) có \(CH\) là đường trung tuyến.

 b) Độ dài đường trung tuyến \(CH\) bằng \(30\sqrt 3 {\rm{ cm}}\).

 c) Độ dài cạnh \(SH\) nhỏ hơn độ dài cạnh \(CH\).

 d) Diện tích xung quanh của hình chóp là \(8635{\rm{ c}}{{\rm{m}}^{\rm{2}}}.\)

Tính giá trị của đa thức \(A = 7{x^2}y - 4{x^6} + 3{y^2}z + 4{x^6}\)tại \[x = 2\,;{\rm{ }}y = 1.\]

Kết quả của phép chia \(\left( {5{x^5}{y^4}z + \frac{1}{2}{x^4}{y^2}{z^3} - 2x{y^3}{z^2}} \right):\frac{1}{4}x{y^2}z\) là đa thức bậc mấy?

Giá trị của biểu thức $\mathrm{A}={\left(3\mathrm{x}+1\right)}^2+{\left(3\mathrm{x}–1\right)}^2–2\left(3\mathrm{x}–1\right)\left(3\mathrm{x}+1\right)$ bằng

Cho biểu thức \[{x^3} + 6{x^2} + 12x + m\] là lập phương của một tổng. Tính giá trị của \(m\).

Sau khi rút gọn biểu thức \(\frac{{1 - x}}{{{x^3}}} \cdot \left( {{x^2} + x + 1 - \frac{{{x^3}}}{{x - 1}}} \right)\) (với \[x \ne 0,\,\,x \ne 1\]), ta được phân thức có tử thức là bao nhiêu?

Kết quả của phép tính \(\frac{{x + 1}}{{x - 2}} + \frac{{x - 2}}{{x + 2}} + \frac{{x - 14}}{{{x^2} - 4}}\) là bao nhiêu?

Bác Mai muốn may một cái lều cắm trại bằng vải bạt có dạng hình chóp tứ giác đều với độ dài cạnh đáy là 2,5 m, chiều cao của cái lều trại là 3 m. Tính thể tích khoảng không bên trong lều theo đơn vị \[{\rm{c}}{{\rm{m}}^3}.\]

Bộ nam châm xếp hình có dạng hình chóp tam giác đều (như hình ảnh) có độ dài cạnh đáy khoảng 6 cm và mặt bên có đường cao khoảng 7 cm. Tính diện tích xung quanh bộ nam châm xếp hình đó theo đơn vị \[{\rm{c}}{{\rm{m}}^{\rm{2}}}\].

Tứ giác \[ABCD\] có số đo các góc \[\widehat A\,;\,\,\widehat B\,;\,\,\widehat C\,;\,\,\widehat D\] tỉ lệ thuận với \[4\,;\,\,3\,;\,\,5\,;\,\,6\]. Tính số đo \[\widehat A\] (đơn vị: độ).

Cho hình vẽ, biết \[\widehat B + \widehat D = 135^\circ \,,\,\,\widehat {BAD} = \frac{{7x}}{2}\].

Tính số đo góc \[\widehat {{C_1}}\] (đơn vị: độ).