Đề cương ôn tập cuối kì 1 Toán 8 Cánh diều cấu trúc mới (Tự luận) có đáp án - Phần 3

Cho hình chóp tam giác đều \(S.ABC\) có các mặt bên cũng là các tam giác đều. Gọi \(SO\) là đường cao của hình chóp, \(OC = 2\sqrt 3 {\rm{\;cm}}.\) Tính (làm tròn các kết quả đến chữ số thập phân thứ hai):

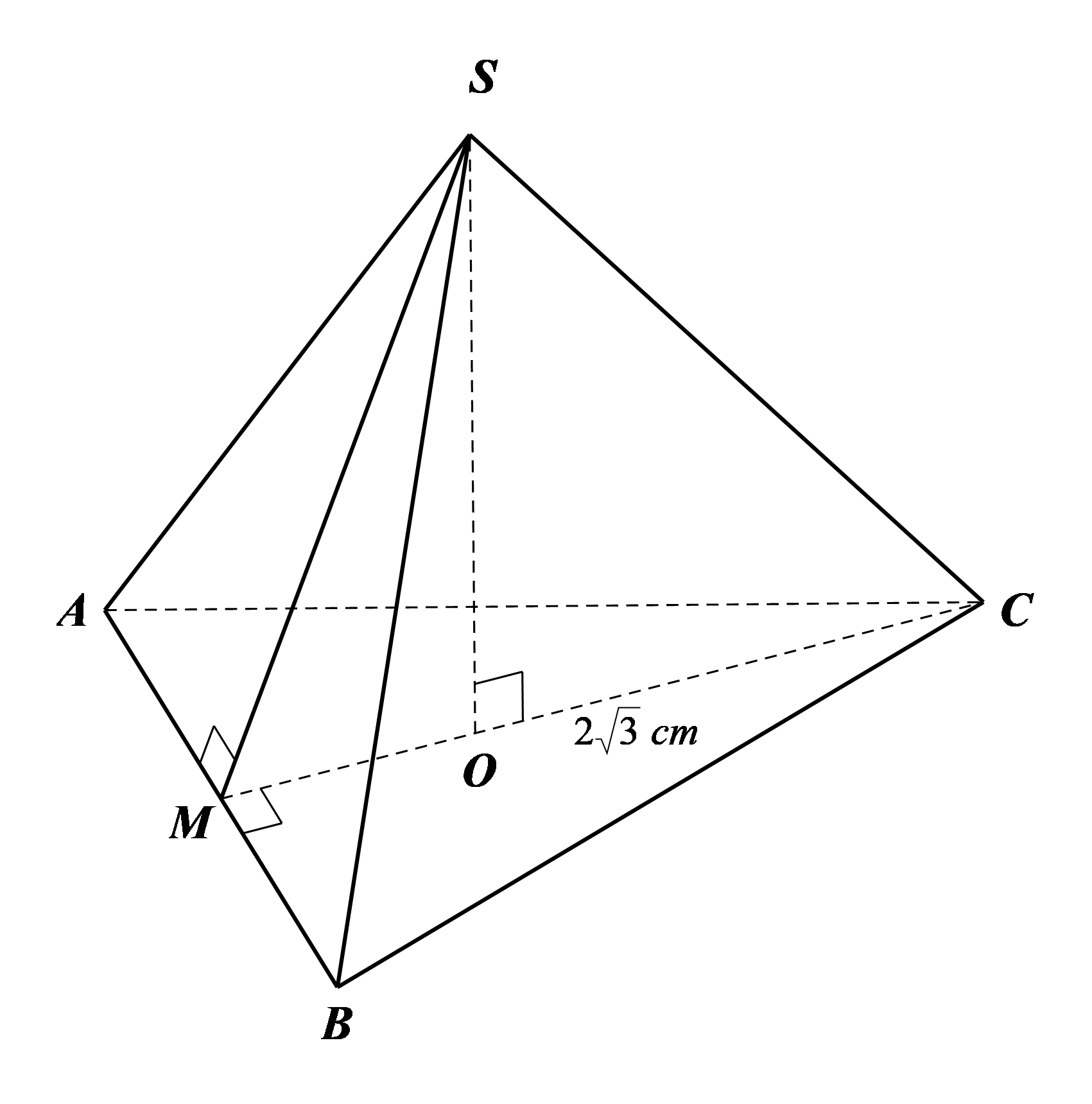
a) Độ dài các cạnh bên của hình chóp.

b) Diện tích xung quanh của hình chóp.

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\) và các mặt bên là những tam giác đều. Tính diện tích xung quanh và thể tích của hình chóp.

(1,5 điểm) Một chiếc lều có dạng hình chóp tứ giác đều ở trại hè của học sinh có kích thước như hình bên.

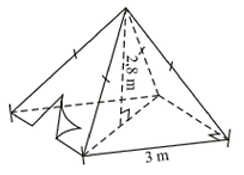
a) Tính thể tích không khí bên trong chiếc lều.

b) Tính số tiền mua vải phủ bốn phía và trải nền đất cho chiếc lều (coi các mép nối không đáng kể). Biết chiều cao của mặt bên xuất phát từ đỉnh của chiếc lều là \(3,18\;\;{\rm{m}}\) và giá vải là \(15\,\,000\) đồng/m². Ngoài ra, nếu mua vải với hóa đơn trên \(20\) m² thì được giảm giá \(5\% \) trên tổng hóa đơn.

Bạn Nam đo một chiếc đèn thả trang trí như hình vẽ bên thì nhận thấy các cạnh đều có cùng độ dài là 20 cm.

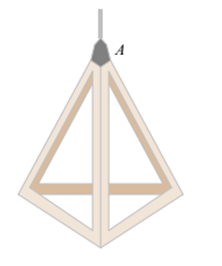
a) Tính độ dài trung đoạn của hình chóp.

b) Tính diện tích xung quanh của chiếc đèn.

c) Bạn Nam đọc và thấy rằng khi treo đèn thì khoảng cách từ đáy của đèn cách mặt trền là 1 m là tốt nhất. Vậy bạn Nam cần đưa đoạn dây điện từ đầu đèn (vị trí \(A)\) tới mặt trần là bao nhiêu (làm tròn kết quả đến hàng phần mười)?

Cho tam giác \(ABC\) vuông tại \(A,\) đường trung tuyến \(AM.\) Gọi \(D\) là trung điểm của \(AB.\) Trên tia đối của tia \(DM\) lấy điểm \(E\) sao cho \(DE = DM.\)

     a) Các tứ giác \(AEBM\) và \(ACME\) là hình gì? Tại sao?

     b) Tam giác vuông \(ABC\) có điều kiện gì thì \(AEBM\) là hình vuông?

Cho tam giác \[ABC\] vuông tại \[A\] có\[AB < AC,\] đường cao\[AH.\] Kẻ \[HD\] vuông góc với\[AB\] tại \(D,\)\[HE\] vuông góc với \[AC\] tại \(E.\)

     a) Tứ giác \[ADHE\] là hình gì? Vì sao?

     b) Tính diện tích của tứ giác \[ADHE\] nếu \[AD = 4\,\,{\rm{cm}};\,\,AH = 5\,\,{\rm{cm}}{\rm{.}}\]

     c)Lấy hai điểm \(I\) và \(K\) sao cho \(D\) là trung điểm của \(BI\) và \(D\) cũng là trung điểm của \(HK.\) Chứng minh tứ giác \[BKIH\]là hình bình hành và\[AK\] vuông góc với \[IH.\]

Cho tam giác \[ABC\] có các đường trung tuyến \[BD,{\rm{ }}CE\] cắt nhau tại \[G.\] Gọi \[F,{\rm{ }}H\] lần lượt là trung điểm của \[BG,{\rm{ }}CG.\]

     a) Tứ giác \[EFHD\] là hình gì? Vì sao?

     b) Tìm điều kiện của tam giác \[ABC\] để tứ giác \[EFHD\] là hình vuông.

Cho hình vuông \[ABCD.\] Lấy điểm \[M\] thuộc đường chéo \[BD.\] Kẻ \[ME\] vuông góc với \(AB\) tại \[E,{\rm{ }}MF\] vuông góc với \[AD\] tại \[F.\]

     a) Tứ giác \(AEMF\) là hình gì? Vì sao?

     b) Xác định vị trí của điểm \[M\] trên đường chéo \[BD\] để diện tích của tứ giác \[AEMF\] lớn nhất.

Cho \(\Delta ABC\) vuông tại \(A\,\,\left( {AB < AC} \right)\), \(E\) là trung điểm của \(BC\). Kẻ \(EF\) vuông góc với \(AB\) tại \(F\), \(ED\) vuông góc với \(AC\) tại \(D\). Gọi \(O\) là giao điểm của \(AE\) và \(DF\)

     a) Chứng minh rằng tứ giác \(ADEF\) là hình chữ nhật.

     b) Lấy điểm \(K\) sao cho \(D\) là trung điểm của \(EK\). Chứng minh tứ giác \(AECK\) là hình thoi.

     c) Chứng minh rằng ba điểm \(B,O,K\) thẳng hàng.

     d) Kẻ \(EM\) vuông góc với \(AK\) tại \(M\). Chứng minh \(\widehat {DMF} = 90^\circ \).

Cho hình bình hành \(ABCD\). Lấy điểm \(K\) và \(E\) trên đường chéo \(BD\) sao cho \(DK = BE\).

     a) Chứng minh \(\Delta ADK = \Delta CBE\).

     b) Chứng minh rằng tứ giác \(AKCE\) là hình bình hành.

     c) Đường thẳng \(AK\) cắt cạnh \(CD\) tại \(M,\) đường thẳng \(CE\) cắt cạnh \(AB\) tại \(N,\)\(AC\) cắt \(BD\) tại \(O.\) Chứng minh ba điểm \(M,O,N\) thẳng hàng.

     d) Hình bình hành \(ABCD\) cần thêm điều kiện gì để hình bình hành \(AKCE\) là hình thoi?

Cho hình chữ nhật \(ABCD\), kẻ \(AH,CK\) vuông góc với \(BD\) \(\left( {H,\,\,K \in BD} \right)\).

     a) Chứng minh \(DH = BK\).

     b) Chứng minh tứ giác \(AHCK\) là hình bình hành.

     c) Gọi \(E\) là điểm đối xứng với \(A\) qua \(H\). Chứng minh \(DECB\) là hình thang cân.

Tìm giá trị nhỏ nhất của các biểu thức sau:

            a) \(A = {\left( {y + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {y - 3} \right)^2} - {\left( {y + 4} \right)^2}\).

Tìm giá trị nhỏ nhất của các biểu thức sau:

b) \[B = {x^2} + 4xy + 5{y^2} - 6y + 11\].

Tìm giá trị nhỏ nhất của các biểu thức sau:

c) \[C = {x^2} - 2xy + 2{y^2} + 2x - 10y + 17\].

Tìm giá trị nhỏ nhất của các biểu thức sau:

d) \(D = \left( {x - 3} \right)\left( {x - 5} \right)\left( {{x^2} - 8x + 17} \right)\).

Tìm giá trị nhỏ nhất của các biểu thức sau:

e) \(E = \frac{{14}}{{{x^2} - 2x + 4}}.\)

Rút gọn các phân thức sau:

            a) \(A = \frac{{{x^3} + {y^3} + {z^3} - 3xyz}}{{{x^2} + {y^2} + {z^2} - xy - yz - xz}}.\)

Rút gọn các phân thức sau:

b) \(B = \frac{{{x^{24}} + {x^{20}} + {x^{16}} + ... + {x^4} + 1}}{{{x^{26}} + {x^{24}} + {x^{22}} + ... + {x^2} + 1}}.\)

Cho x và y thoả mãn: \({x^2} + 5{y^2} - 3xy - 3x - y + 5 = 0\). Tính giá trị của biểu thức:

\(A = \frac{{{{\left( {x + y - 4} \right)}^{2222}} - {y^{2222}}}}{x}.\)

Cho x và y thoả mãn: \[{x^2} + 2xy + 6x + 6y + 2{y^2} + 8 = 0\]. Tìm giá trị lớn nhất và nhỏ nhất của biểu thức \[M = x + y + 6\].

Chứng minh rằng

     a) Nếu \[x\] là số tự nhiên không chia hết cho \[3\] thì \(M = 2{x^2} - 5\) chia hết cho \[3\] .

     b) Nếu \(x\) là số tự nhiên lẻ thì \(N = {x^3} + 3{x^2} - x - 3\) chia hết cho \[8\] .

     c) Đa thức \[M = x\left( {x + 1} \right)\left( {x + 2} \right)\left( {x + 3} \right) + 1\] (với \(x \in \mathbb{Z}\)) là bình phương của một số nguyên.

Cho ba số thực \(a,\,\,b,\,\,c\) khác \(2\) và thỏa mãn \(a + b + c = 6.\) Tính giá trị của biểu thức:

\(M = \frac{{{{\left( {a - 2} \right)}^2}}}{{\left( {b - 2} \right)\left( {c - 2} \right)}} + \frac{{{{\left( {b - 2} \right)}^2}}}{{\left( {a - 2} \right)\left( {c - 2} \right)}} + \frac{{{{\left( {c - 2} \right)}^2}}}{{\left( {a - 2} \right)\left( {b - 2} \right)}}.\)

Cho ba số thực \(x,y,z \ne 0\) và \(x + y + z = 0\). Tính giá trị của biểu thức

\(T = \frac{{xy}}{{{x^2} + {y^2} - {z^2}}} + \frac{{yz}}{{{y^2} + {z^2} - {x^2}}} + \frac{{xz}}{{{z^2} + {x^2} - {y^2}}}\).

Bác Bảy có một trang trại lớn để trồng rau và chăn nuôi gia cầm. Bác dự định mua một tấm lưới thép B40 để rào bao quanh khu vực nuôi gia cầm của trang trại với thiết kế có dạng hình chữ nhật \(ABCD\)(như hình mô tả ở bên). Biết rằng, bác Bảy không rào xung quanh khu vực nhà kho và vị trí nhà kho cố định. Với số tiền của mình, bác Bảy chỉ mua được tấm lưới có chiều dài \(500\,\,{\rm{m}}\). Hỏi bác Bảy sẽ dựng rào chắn như thế nào để diện tích khu nuôi gia cầm là lớn nhất?

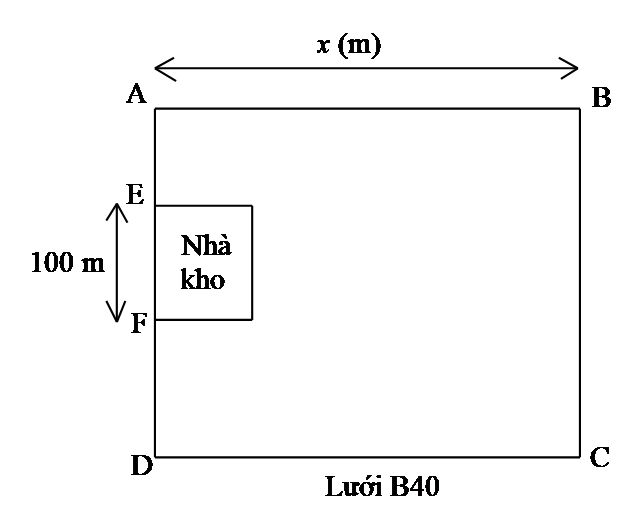
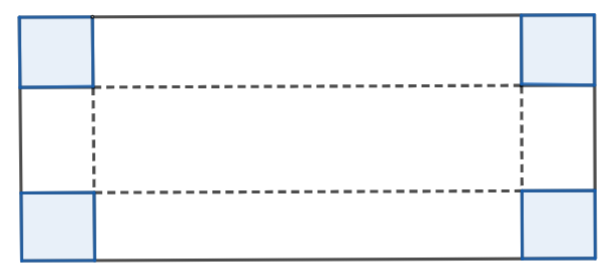
Một tấm bìa cứng hình chữ nhật có chiều dài là \({\rm{50 cm}}\) và chiều rộng là \({\rm{30 cm}}\). Bạn Linh cắt ở mỗi góc một tấm bìa hình vuông cạnh \(x{\rm{\;(cm)}}\) và xếp phần còn lại thành một hình hộp không nắp. Tìm \(x\) để diện tích xung quanh của hình hộp chữ nhật sau khi cắt là lớn nhất.