Bộ 3 đề thi giữa kì 1 Toán 7 Kết nối tri thức có đáp án - Đề 3
23 câu hỏi
A. TRẮC NGHIỆM (7,0 điểm)
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Cách viết nào sau đây biểu diễn một số hữu tỉ?
\(\frac{{6,5}}{{14}}.\)
\(\frac{3}{7}.\)
\(\frac{{21}}{0}.\)
\(\frac{{15}}{{0,2}}.\)
Trong các khẳng định sau, khẳng đính nào sai?
\({x^1} = x.\)
\({x^0} = 1{\rm{ }}\left( {x \ne 0} \right)\).
\({x^1} = 1.\)
\({x^{a + 1}} = {x^a}.x\).
Chọn phát biểu đúng. Với \(a,b,c \ne 0\)
Nếu \(a + b = c\) thì \(a = c - b.\)
Nếu \(a + b = c\) thì \(a = c + b.\)
Nếu \(a + b = c\) thì \(a = b - c.\)
Nếu \(a + b = c\) thì \(a = - c - b.\)
Số thập phân \(0,36363636.....\) được viết dưới dạng thu gọn (có chu kì trong dấu ngoặc) là
\(0,\left( {363} \right).\)
\(0,\left( {36} \right).\)
\(0,\left( 3 \right).\)
\(0,3\left( {63} \right)\).
Trong các số sau, đâu là số vô tỉ?
\(\sqrt {121} .\)
\(0,\left( {12} \right).\)
\(0,010010001...\)
\( - 3,12\left( {345} \right).\)
Căn bậc hai số học của \(81\) là
\(9\) và \( - 9\).
\(\frac{1}{{81}}.\)
\(9.\)
\(\frac{{81}}{2}.\)
Tập hợp các số thực có kí hiệu là
\(\mathbb{R}.\)
\(\mathbb{Q}.\)
\(\mathbb{Z}.\)
\(\mathbb{N}.\)
Trong các mệnh đề sau, mệnh đề nào đúng?
Nếu \(x \in \mathbb{Z}\) thì \(x \in \mathbb{R}\).
Nếu \(x \in \mathbb{R}\) thì \(x \in \mathbb{Q}\).
Nếu \(x \in \mathbb{Q}\) thì \(x \in \mathbb{Z}\).
Nếu \(x \in \mathbb{Z}\) thì \(x \in \mathbb{N}.\)
Quan sát hình vẽ. Góc kề bù với \(\widehat {xEn}\) là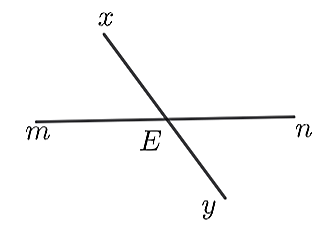
\(\widehat {mEy}.\)
\(\widehat {mEx}.\)
\(\widehat {nEy}.\)
\(\widehat {mEx}\) và \(\widehat {nEy}.\)
Chọn phát biểu đúng trong các phát biểu dưới đây:
\(\widehat {{H_1}}\) và \(\widehat {{K_1}}\) là hai góc so le trong.
\(\widehat {{H_4}}\) và \(\widehat {{K_4}}\) là hai góc đồng vị.
\(\widehat {{H_3}}\) và \(\widehat {{K_4}}\) là hai góc so le trong.
\(\widehat {{H_4}}\) và \(\widehat {{K_2}}\) là hai góc so le trong.
Cho đường thẳng \(c\) cắt hai đường thẳng \(a\) và \(b\) phân biệt và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì
\(a\) song song với \(b.\)
\(a\) cắt \(b.\)
\(a\) vuông góc với \(b\).
\(a\) trùng với \(b\).
Phát biểu đúng về tiên đề Euclid là
Qua một điểm ở ngoài một đường thẳng, chỉ có một đường thẳng song song với đường thẳng đó.
Qua một điểm ở ngoài một đường thẳng, có vô số đường thẳng song song với đường thẳng đó.
Qua một điểm ở ngoài một đường thẳng, không kẻ được đường thẳng song song với đường thẳng đó.
Qua một điểm ở ngoài một đường thẳng, kẻ được ít nhất một đường thẳng song song với đường thẳng đó.
Phần 2. (2,0 điểm) Câu trắc nghiệm đúng sai
Trong câu 13, 14, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d).
Vào dịp Tết Nguyên Đán, bà và Thảo cùng nhau gói bánh chưng. Nguyên liệu để gói bánh chưng gồm bột nếp, đậu xanh, thịt lợn và lá dong. Mỗi chiếc bánh sau khi gói nặng khoảng \(0,8\) kg gồm: \(0,5\) kg gạo; \(0,125\) kg đậu xanh; \(0,04\) kg lá dong và còn lại là thịt.
a) Khối lượng thịt trong mỗi cái bánh chưng là \(125\) g.
b) Khối lượng gạo trong bánh chưng là nhiều nhất.
c) Trong mỗi cái bánh chưng, tổng khối lượng đậu xanh, gạo và thịt gấp \(19\) lần khối lượng lá dong.
d) Nếu khối lượng bánh sau khi gói là \(6,4\)kg thì có nghĩa là bà và Thảo đã gói được \(80\) cái bánh chưng.
Cho hình vẽ, biết \(\widehat {xAB} = 70^\circ ,\widehat {ACB} = 55^\circ \), tia \(AC\) là tia phân giác của \(\widehat {yAB}\).
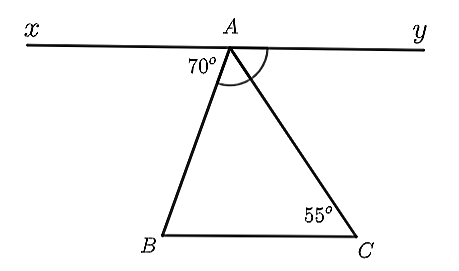
Xét tính đúng sai của các khẳng định dưới đây:
a) \(\widehat {xAB}\) và \(\widehat {CAB}\) là hai góc kề bù.
b) \(\widehat {yAB} = 2\widehat {BAC}\).
c) \(\widehat {yAC} = 60^\circ \).
d) \(xy\parallel BC\).
Phần 3. (2,0 điểm) Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Tính giá trị của \(x\), biết: \(\frac{2}{3}x + \frac{7}{{10}} = \frac{3}{{10}}\).
(Kết quả ghi dưới dạng số thập phân)
Cho các phân số \(\frac{5}{8};{\rm{ }} - \frac{3}{{20}};{\rm{ }}\frac{4}{{11}};{\rm{ }}\frac{{15}}{{22}};{\rm{ }} - \frac{7}{{12}};{\rm{ }}\frac{{14}}{{35}}\). Hỏi có bao nhiêu phân số viết được dưới dạng số thập phân vô hạn tuần hoàn?
Tìm giá trị của \(x\), biết: \(\sqrt {0,81} .\left( {x + \sqrt {\frac{{16}}{{25}}} } \right) = \frac{9}{{10}}\).
(Kết quả ghi dưới dạng số thập phân)
Cho hình vẽ, biết \(\widehat {aBE} = 60^\circ \), \(\widehat {BED} = 60^\circ \); \(\widehat {BCD} = 135^\circ \).
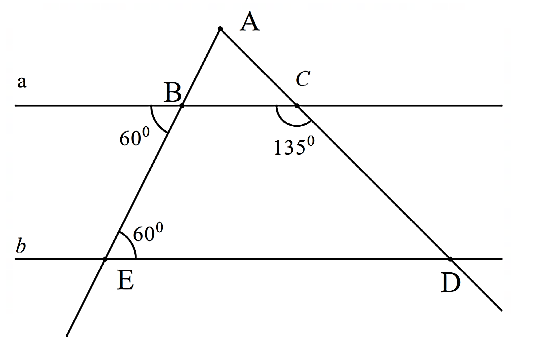
Hỏi số đo \(\widehat {CDE}\) bằng bao nhiêu độ?
B. TỰ LUẬN (3,0 điểm)
(1,0 điểm). Thực hiện phép tính:
a) \(\frac{{13}}{{25}} - \frac{{11}}{4} - \frac{{38}}{{25}} + \frac{{15}}{4} + \frac{1}{2}\); b) \({\left( {\frac{1}{2} - \frac{2}{3}} \right)^2} + 1\frac{2}{3}:\left| { - 0,75} \right| - \sqrt {\frac{1}{{16}}} \).
a) Tính \(\widehat {zOy}\).
b) Trên nửa mặt phẳng bờ \(Ox\) chứa \(Oz\), vẽ tia \(Ot\) sao cho \(\widehat {xOt} = 140^\circ \). Chứng minh \(Oz\) là tia phân giác của \(\widehat {xOt}\).
c) Vẽ tia \(Om\) là tia đối của tia \(Oz\), tia \(On\) là tia đối của tia \(Ot\). Tính \(\widehat {yOm}\) và so sánh với \(\widehat {xOn}\).
(0,5 điểm). Bình đọc một cuốn sách trong 4 ngày. Ngày thứ nhất đọc được \(\frac{1}{6}\) cuốn sách, ngày thứ hai đọc được \(\frac{1}{4}\) cuốn sách, ngày thứ ba đọc được \(\frac{1}{5}\) cuốn sách. Hỏi hai ngày đầu Bình đọc nhiều hơn hay ít hơn hai ngày sau? Tìm phân số thể hiện sự chênh lệch đó.








