Bộ 10 đề thi giữa kì 1 Toán 7 Kết nối tri thức có đáp án - Đề 8
13 câu hỏi
Cách viết nào sau đây là đúng?
\[2,\left( 1 \right) \notin \mathbb{Q}\]
\(\frac{1}{2} \in \mathbb{Z}\)
\( - 8 \in \mathbb{N}\)
\(\frac{{ - 3}}{5} \notin \mathbb{Q}\).
Cho trục số như hình vẽ
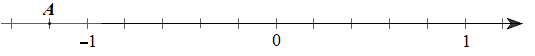
Điểm \(A\) biểu diễn số hữu tỉ:
\(\frac{{ - 4}}{5}\)
\(\frac{{ - 5}}{4}\)
\(\frac{{ - 6}}{5}\)
\(\frac{{ - 1}}{5}\).
Phân số nào sau đây viết được dưới dạng số thập phân hữu hạn?
\(\frac{3}{7}\)
\(\frac{6}{{15}}\)
\(\frac{{ - 1}}{6}\)
\(\frac{7}{{12}}\).
Cho \(a = 0,\left( {53} \right)\) và \(b = 0,53\). Khẳng định nào sau đây là đúng?
\(a = b\)
\(a \approx b\)
\(a > b\)
\(a < b\).
Khẳng định nào sau đây là đúng?
Hai góc có chung đỉnh thì bằng nhau;
Hai góc bằng nhau và có một cạnh của góc này là tia đối của một cạnh của góc kia là hai góc đối đỉnh
Hai góc bằng nhau có đỉnh chung là hai góc đối đỉnh
Hai góc đối đỉnh thì bằng nhau.
Cho hình vẽ bên.
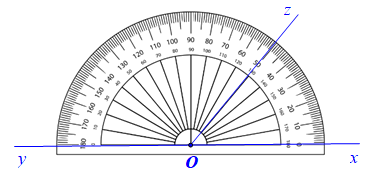
Số đo của góc bù với góc \(yOz\) trong hình là
\(25^\circ \)
\(50^\circ \)
\(65^\circ \)
\(130^\circ \).
Đường thẳng \(a\) cắt hai đường thẳng \(b\), \(c\) và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì
\(b \bot c\)
\(b\,{\rm{//}}\,c\)
\(b\) trùng \(c\)
\(b\) cắt \(c\).
Cho các đường thẳng phân biệt \(a\,{\rm{//}}\,b,\,\,b\,{\rm{//}}\,c\) và \(d \bot a\). Lập luận nào sau đây là sai?
\(a\,{\rm{//}}\,c\) vì cùng vuông góc với \(b\)
\(a\,{\rm{//}}\,c\) vì cùng song song với \(b\)
\(d \bot b\) vì \(d \bot a\) và \(a\,{\rm{//}}\,b\)
\(d \bot c\) vì \(d \bot b\) và \(b\,{\rm{//}}\,c\).
(2,0 điểm) Tính giá trị của các biểu thức sau (tính hợp lí nếu có thể):
(a) \(\frac{4}{5} + \frac{3}{5}.\left( { - \frac{2}{{15}}} \right)\)
(b) \(\frac{{{9^3}{{.3}^2}}}{{{3^6}}}\)
(c) \(\sqrt {\frac{{196}}{{121}}} :\frac{7}{{11}} - \left| {\frac{{ - 5}}{4}} \right|\)
(d) \(\frac{{ - 5}}{{17}}.\frac{{31}}{{33}} - \frac{5}{{17}}.\frac{2}{{33}} + 1\frac{5}{{17}}\).
(2,0 điểm) Tìm x, biết:
(a) \(\frac{3}{7} + \frac{4}{7}x = \frac{1}{3}\)
(b) \({\left( {\frac{{ - 2}}{3}} \right)^x} = \frac{{ - 32}}{{243}}\)
(c) \(10\sqrt x - 5 = 25\)
(d) \({\left( {\frac{1}{2}x - \frac{3}{4}} \right)^2} - 1 = \frac{{ - 3}}{4}\).
(1,5 điểm) Một người có 150 triệu đồng muốn đi gửi tiết kiệm.
(a) Nếu người đó gửi tiền ở ngân hàng \(A\) thì được nhận lãi suất \[7\% \] một năm. Hỏi sau một năm thì người đó nhận về được bao nhiêu tiền? (cả số tiền gốc và số tiền lãi)
(b) Nếu người đó gửi tiền ở ngân hàng \[B\] thì được nhận lãi suất \[6\% \] một năm và được nhận ngay 2 triệu đồng. Hỏi người đó nên gửi tiền ở ngân hàng nào để có số tiền nhận được sau một năm nhiều hơn?
(2,0 điểm) Cho hình vẽ biết \(xx' \bot tt'\), \[yy' \bot tt'\], \(\widehat {zCx'} = 110^\circ \), \(\widehat {CAO} = 50^\circ \), \(\widehat {OBy'} = 140^\circ \).
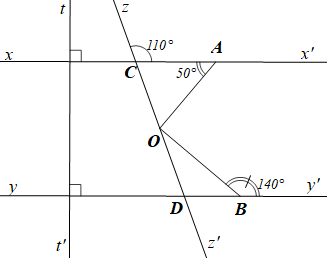
(a) Vẽ lại hình (đúng số đo của các góc) và viết giả thiết, kết luận của bài toán.
(b) Giải thích tại sao \(xx'\,{\rm{//}}\,yy'\).
(c) Tìm số đo của \(\widehat {CDy}\).
(d) Tìm số đo của \(\widehat {AOB}\).
(0,5 điểm) Tìm \(a,\,b\) thỏa mãn \({\left( {2a - b} \right)^{2022}} + {\left| {b + 1} \right|^{2023}} = 0\).








