Bộ 10 đề thi giữa kì 1 Toán 7 Kết nối tri thức có đáp án - Đề 2
18 câu hỏi
Số nào sau đây là số hữu tỉ dương?
\[\frac{{ - 2}}{5}\]
\(\frac{{ - 5}}{{ - 14}}\)
\[ - \frac{3}{{11}}\]
\(\frac{7}{{ - 4}}\).
Khẳng định nào sau đây sai?
Số đối của 18 là −18
Số đối của \(\frac{4}{{15}}\) là \(\frac{{ - 4}}{{15}}\)
Số đối của \(\frac{{11}}{5}\) là \(\frac{{ - 11}}{{ - 5}}\)
Số đối của \(\frac{{ - 23}}{7}\) là \(\frac{{23}}{7}\).
Trong các câu sau đây, câu nào là đúng?
A. \(\frac{{ - 4}}{5} < \frac{{ - 1}}{3} < 0 < 4 < 2,25\)
B. \(\frac{{ - 1}}{3} < \frac{{ - 4}}{5} < 0 < 2,25 < 4\)
C. \[0 < \frac{{ - 1}}{3} < \frac{{ - 4}}{5} < 2,25 < 4\]
D. \(\frac{{ - 4}}{5} < \frac{{ - 1}}{3} < 0 < 2,25 < 4\).
Quan sát trục số và cho biết điểm \(T\) biểu diễn số hữu tỉ nào?

\(\frac{{ - 3}}{5}\)
3
−3
\(\frac{3}{5}\).
Số nào sau đây viết được dưới dạng số thập phân hữu hạn?
1,3(45)
\(\sqrt 3 \)
\(\frac{{ - 5}}{4}\)
\(\frac{{10}}{3}\).
Số \(\sqrt {2022} \) thuộc tập hợp số nào?
\(\mathbb{R}\)
\(\mathbb{N}\)
\(\mathbb{Z}\)
\(\mathbb{Q}\).
Khẳng định đúng là
\(\left| { - 4,25} \right| = - 4,25\)
\(\left| { - 4,25} \right| = 4,25\)
\(\left| { - 4,25} \right| = \pm 4,25\)
\(\left| { - 4,25} \right| > 4,25\).
Giá trị \(x\) thỏa mãn \(\sqrt x = - 9\) là
\(x = 81\)
\(x = - 81\)
\(x = 3\)
Không có giá trị \(x\) thỏa mãn.
Khẳng định nào dưới đây là đúng?
Hai góc đối đỉnh thì bù nhau
Hai góc bằng nhau thì đối đỉnh;
Hai góc đối đỉnh thì bằng nhau
Hai góc đối đỉnh thì phụ nhau.
Trong các cặp góc sau đây, cặp góc bù nhau là
130° và 50°
140° và 70°
50° và 150°
40° và 40°.
Cho \(\widehat {xAy} = 60^\circ \). Trên tia \(Ox,\,\,Oy\) lần lượt lấy hai điểm \(B,\,\,C\) khác điểm \(O\). Từ điểm \(B\) vẽ đường thẳng song song với \(Ax\), từ điểm \(C\) vẽ đường thẳng song song với \(Ay\), chúng cắt nhau tại điểm \(D\). Khi đó, số đo của \(\widehat {BCD}\) là:
120°
60°
50°
Không xác định được.
Trong các câu sau, hãy chọn đáp án đúng:
Định lí là một tính chất được khẳng định là đúng bằng tính toán;
Chứng minh định lí là dùng tính toán để khẳng định kết luận;
Điều cho biết là kết luận, điều suy ra là giả thiết;
Giả thiết của định lý là điều cho biết, kết luận của định lí là điều suy ra.
(0,5 điểm) Viết các số \(\frac{4}{9};\,\,\frac{8}{{27}};\,\,\frac{{32}}{{243}}\) dưới dạng lũy thừa cơ số \(\frac{2}{3}\).
(1,0 điểm) Biết rằng bình phương độ dài đường chéo của một hình chữ nhật bằng tổng bình phương độ dài hai cạnh của nó. Một hình chữ nhật có chiều dài là 10 cm và chiều rộng là 6 cm. Hỏi độ dài đường chéo của hình chữ nhật đó bằng bao nhiêu centimet (làm tròn kết quả đến hàng phần trăm)?
(1,5 điểm) Thực hiện phép tính (tính hợp lí nếu có thể).
(a) \(2\frac{1}{5} + 0,25\,\,.\,\,{\left( {\frac{2}{5}} \right)^2}\);
(b) \(\frac{{ - 3}}{{22}} + \frac{1}{9} + \frac{5}{{22}}\, + \frac{{ - 10}}{9}\);
(c) \(\sqrt {\frac{9}{{64}}} :\frac{5}{4} + \sqrt {\frac{9}{{64}}} \,:\frac{5}{6}\).
(1,5 điểm) Tìm \(x\), biết:
(a) \(\frac{3}{4} - \frac{2}{3}:x = \frac{{ - 1}}{{20}}\)
(b) \(\left| {2x - \frac{5}{6}} \right| - \frac{7}{3} = \frac{{ - 11}}{{18}}\)
(c) \(2{(5 - 4x)^2} - 17 = \frac{{ - 55}}{9}\).
(1,5 điểm) Đường thẳng \(c\) cắt hai đường thẳng \(a\) và \(b\) lần lượt tại hai điểm \(M\) và \(N\). Đường thẳng \(d\) cắt hai đường thẳng \(a\) và \(b\) lần lượt tại hai điểm \(P\) và \(Q\) (như hình vẽ). Biết \({\widehat M_1} = 55^\circ ;\,\,{\widehat N_1} = 55^\circ ;\,\,{\widehat Q_1} = 125^\circ \).
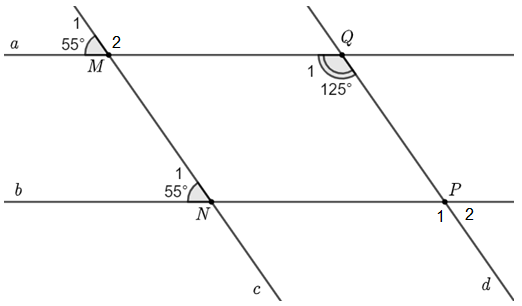
(a) Vẽ lại hình và viết giả thiết, kết luận của bài toán.
(b) Chứng minh \[MQ\parallel NP & ;\,\,MN\parallel PQ\].
(c) Tìm số đo \({\widehat P_2}\).
(1,0 điểm) So sánh \(A = \frac{{1 + {{2022}^{2022}}}}{{1 + {{2022}^{2023}}}}\) và \(B = \frac{{1 + {{2022}^{2023}}}}{{1 + {{2022}^{2024}}}}\).








