Bộ 10 đề thi giữa kì 1 Toán 7 Kết nối tri thức có đáp án - Đề 5
18 câu hỏi
Khẳng định nào sau đây là đúng?
\(0,125 \in \mathbb{Q}\)
\( - 10 \in \mathbb{N}\)
\(5\frac{1}{3} \notin \mathbb{Q}\)
\(3 \notin \mathbb{Z}\).
Số đối của số \( - \frac{{ - 3}}{5}\) là
\(\frac{5}{3}\)
\( - \frac{5}{3}\)
\( - \frac{3}{5}\)
\(\frac{3}{5}\).
Điền dấu thích hợp vào chỗ chấm \(3,25.... - 3\frac{4}{7}\) là
\( \le \)
=
<
>
Các số \( - 2,15;\,\,\frac{5}{4};\,\, - 3\frac{1}{5};\,\,2;\,\,0\) được sắp xếp theo thứ tự giảm dần là
\[2;\,\,\frac{5}{4};\,\,0;\,\, - 2,15;\,\, - 3\frac{1}{5}\]
\[0;\,\,\frac{5}{4};\,\,2;\,\, - 2,15;\,\, - 3\frac{1}{5}\]
\( - 3\frac{1}{5};\,\, - 2,15;\,\,0;\,\,\frac{5}{4};\,\,2\)
\( - 3\frac{1}{5};\,\, - 2,15;\,\,0;\,\,2;\,\,\frac{5}{4}\).
Phân số nào dưới dây được viết dưới dạng số thập phân vô hạn tuần hoàn?
\( - \frac{3}{8}\)
\(\frac{2}{5}\)
\(\frac{{11}}{{45}}\)
\(\frac{{1356}}{{100}}\).
Trong các số dưới đây, số nào là số vô tỉ?
\(\sqrt {25} \)
0,(36)
0,01200001011…
\( - \frac{3}{5}\).
So sánh \(\sqrt {{{( - 5)}^2}} \) và \(\sqrt {27} \):
A. \(\sqrt {{{( - 5)}^2}} < \sqrt {27} \)
B.\(\sqrt {{{( - 5)}^2}} > \sqrt {27} \)
C. \(\sqrt {{{( - 5)}^2}} = \sqrt {27} \)
D. Không so sánh được.
Có bao nhiêu giá trị \(x\) thỏa mãn \(\left( {5x + 3} \right)\left( {7 - \sqrt x } \right) = 0\)?
1
3
4
2.
Hai đường thẳng \(xx'\) và \(yy'\) cắt nhau tại \(O\). Góc đối đỉnh với \[\widehat {yOx'}\] là
\[\widehat {y'Ox'}\]
\[\widehat {y'Ox}\]
\[\widehat {yOx'}\]
\[\widehat {yOx}\].
Cho hai đường thẳng \(ab\) và \(cd\) cắt nhau tại \(O\) sao cho \(\widehat {aOc} = 120^\circ \). Khẳng định nào dưới đây là đúng?
\[\widehat {bOd} = 60^\circ \]
\[\widehat {bOc} = 60^\circ \]
\[\widehat {aOd} = 120^\circ \]
\[\widehat {bOc} = 120^\circ \].
Cho hình vẽ dưới đây biết \[a\,\parallel b\]và \[\widehat {{M_1}} = 45^\circ .\] Khi đó, số đo \[\widehat {{N_1}}\] là
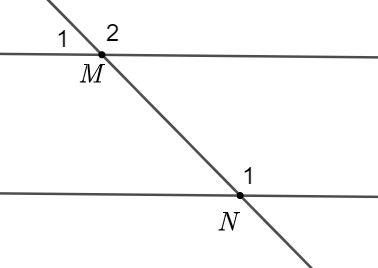
\[45^\circ \]
\[35^\circ \]
\[115^\circ \]
\[135^\circ \].
Trong những câu dưới đây, câu nào không phải là định lí?
Hai góc đối đỉnh thì bằng nhau;
Hai góc kề nhau thì có tổng số đo là \[180^\circ \]
Nếu hai đường thẳng song song cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau
Đường thẳng vuông góc với một trong hai đường thẳng song song thì đường thẳng đó vuông góc với đường thẳng còn lại.
(1,5 điểm)
1. Tìm số đối của các số\( - 1;\,\,\frac{{11}}{3};\,\, - 0,5;\,\,1\frac{2}{3}\).
2. Tính diện tích của mảnh vườn hình chữ nhật có chiều dài là 12,34 m và chiều rộng là 5,67 m (làm tròn đến hàng phần mười).
(2,0 điểm) Thực hiện các phép tính (tính hợp lí nếu có thể).
(a) \[\frac{2}{3} - \frac{{ - 3}}{7}\];
(b) \[\frac{2}{3} + \frac{4}{5}:\frac{{ - 3}}{5}\];
(c) \[3\frac{1}{2} + \frac{7}{3}:\frac{{ - 5}}{3} - 0,4\];
(d) \(9,125 + \left[ {0,25 - \left( {8,125 - 5,25} \right)} \right]\).
(1,0 điểm) Tìm \(x\), biết:
(a) \(\frac{1}{4}x - \frac{1}{3} = - \frac{5}{9}\) ;
(b) \({2^{x + 3}} - {3.2^x} = 320\).
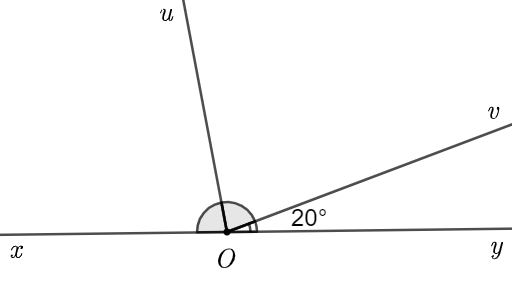
(1,0 điểm) Cho hình vẽ sau. Biết \(\widehat {xOy}\) là góc bẹt và \(Ou\) là tia phân giác của \(\widehat {xOv}\). Tính số đo \(\widehat {uOv}\).
(2,5 điểm) Cho tam giác \(ABC\) vuông tại \(A\). Qua đỉnh \(B\) của tam giác kẻ đường thẳng \(ab\) vuông góc với cạnh \(AB\) (\(AC,\,\,Bb\) thuộc cùng một nửa mặt phẳng có bờ là đường thẳng chứa cạnh \(AB\)).
(a) Chứng minh \[a\,b\parallel AC\].
(b) Biết \[\widehat {CBb} = 35^\circ \]. Tính số đo các góc trong tam giác \(ABC\).
(1,0 điểm) Cho biểu thức \[A = 2 + {2^2} + {2^3} + ...... + {2^{2022}}\].
Tìm \(x\) biết: \(2\left( {A + 2} \right) = {2^{2x}}\).








