Bộ 10 đề thi giữa kì 1 Toán 7 Kết nối tri thức có đáp án - Đề 3
18 câu hỏi
Trong các số sau đây, số không phải là số hữu tỉ?
\[3\frac{1}{5}\]
\(\frac{{ - 8}}{{13}}\)
\[\frac{7}{0}\]
2,5.
Giá trị tuyệt đối của \(\frac{{ - 25}}{8}\) là
\(\frac{{25}}{8}\)
\(\frac{8}{{25}}\)
\(\frac{{25}}{{ - 8}}\)
\(\frac{{ - 8}}{{25}}\).
Dấu cần điền vào chỗ chấm \(\frac{{ - 32}}{5}..... - 6,5\) là
A. <
B. >
C. =
D. \( \le \).
Cách biểu diễn số \(\frac{5}{3}\) trên trục số nào dưới đây là đúng?

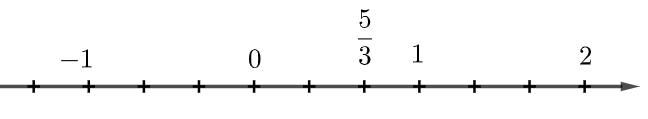

 .
.
Số nào sau đây viết được dưới dạng số thập phân vô hạn tuần hoàn?
3,25
\(\frac{7}{6}\)
\(\sqrt {11} \)
\(3\frac{2}{5}\).
Giá trị của biểu thức \(M = - \sqrt {114} \) là
−12
−12 hoặc 12
\( \pm 12\)
12.
Số đối của số \[ - \sqrt {15} \] là
\[\frac{{ - 1}}{{\sqrt {15} }}\]
\[\frac{1}{{\sqrt {15} }}\]
\[\frac{1}{{ - \sqrt {15} }}\]
\[\sqrt {15} \].
Dãy số sau đây được sắp xếp theo thứ tự tăng dần?
\( - 4;\,\,\sqrt 3 ;\,\,0;\,\,2,(45);\,\,\frac{3}{8}\)
\( - 4;\,\,0;\,\,2,(45);\,\,\sqrt 3 ;\,\,\frac{3}{8}\)
\( - 4;\,\,0;\,\,\frac{3}{8};\,\,\sqrt 3 ;\,\,2,(45)\)
\[2,(45);\,\,\sqrt 3 ;\,\,\frac{3}{8};\,\,0;\,\, - 4\].
Cho \(\widehat {aOb}\) đối đỉnh với \(\widehat {a'Ob'}\) và \(\widehat {aOb} = 40^\circ \). Khi đó, số đo \(\widehat {a'Ob'}\) là
40°
140°
60°
Một giá trị khác.
Cho hai đường thẳng \(xx'\) và \(yy'\) cắt nhau tại điểm \(O\). Góc kề bù với \(\widehat {xOy}\) là
\(\widehat {x'Oy'}\)
\(\widehat {xOx'}\)
\(\widehat {yOy'}\)
\(\widehat {xOy'}\).
Tìm số đo góc \(x\) trong hình vẽ bên là
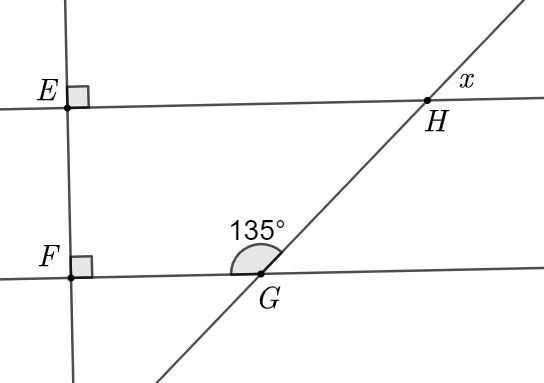
135°
45°
90°
Không xác định được.
Chứng minh định lí là
Dùng hình vẽ để từ giả thiết suy ra kết luận
Dùng đo đạc thực tế để suy ra kết luận từ giả thiết
Dùng lập luận để từ giả thiết suy ra kết luận
Cả A, B, C đều sai.
(1,5 điểm)
1. Tìm số đối của các số \(2;\,\,\frac{{ - 1}}{5};\,\, - 4,5;\,\,4\frac{2}{3}\).
2. Một chiếc ti vi có đường chéo dài 43 inch. Độ dài đường chéo của máy ti vi này theo đơn vị cm với độ chính xác \(d = 0,05\) (cho biết 1 inch \( \approx \) 2,54 cm) là bao nhiêu?
(2,0 điểm) Thực hiện phép tính (tính hợp lí nếu có thể).
(a) \(\frac{{ - 8}}{{15}} + \frac{1}{{25}} - \frac{7}{{15}}\);
(b) \[\frac{2}{{11}}\,\,.\,\,\frac{{ - 3}}{{17}} - \frac{{14}}{{17}}\,\,.\,\,\frac{2}{{11}} + 3\frac{2}{{11}}\];
(c) \[{\left( {\frac{1}{3}} \right)^{14}}:{\left( {\frac{1}{3}} \right)^{12}} - \left[ {\frac{5}{4} - \left( {\sqrt {16} - \frac{2}{3}} \right)} \right]\];
(d) \(24\,\,.\,\,{\left( {\frac{1}{4}} \right)^2} + \left| {\frac{{ - 2}}{3}} \right|\,\,.\,\,\sqrt {\frac{{81}}{{64}}} - {\left( {\frac{{31}}{{19}}} \right)^0}\).
(1,0 điểm) Tính giá trị biểu thức biết:
(a) \(A = 5{x^3} - \frac{1}{2}{x^2} - 4\left| x \right| + 1\) với \(x = \frac{{ - 1}}{5}\);
(b) \(B = 2\left| x \right| - \frac{{{y^2}}}{3} - 12\) với \(x = 5;\,\,y = \frac{1}{3}\).
(0,5 điểm) Cho góc bẹt \(\widehat {xOy}\). Vẽ tia \(Oz\) sao cho \(\widehat {xOz} = 80^\circ \). Trên mặt phẳng bờ \(Ox\) chứa tia \(Oz\) vẽ tia \(Ot\) sao cho \[\widehat {xOt} = 160^\circ \]. Chứng tỏ \(Oz\) là tia phân giác của \(\widehat {xOt}\).
(1,0 điểm) Cho hai đường thẳng \(a\) và \(b\) song song với nhau. Trên đường thẳng \(a\) lấy hai điểm \(A\) và \(E\) (điểm \(A\) không trùng với điểm \(E\)). Kẻ \(AB\) vuông góc với đường thẳng \(b\) tại \(B\). Lấy điểm \(D\) thuộc đường thẳng \(b\) sao cho \(\widehat {AED} = 65^\circ .\)
(a) Vẽ hình và viết giả thiết, kết luận của bài toán.
(b) Tính số đo của \(\widehat {BAE}\) và \(\widehat {BDE}\).
(1,0 điểm) Một cửa hàng nhập về 100 cái áo với giá gốc 200 000 đồng/cái. Cửa hàng đã bán 80 cái áo với giá mỗi cái áo lãi 20% so với giá gốc; 20 cái áo còn lại mỗi cái bán lỗ 10% so với giá gốc. Hỏi sau khi bán hết 100 cái áo cửa hàng đó lãi hay lỗ bao nhiêu tiền?








