Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án (Đề 11)
22 câu hỏi
Tập xác định của hàm số \(y = \sqrt[3]{{\sin 2{\rm{x}} - \tan x}}\) là:
\(D = \left\{ {x \in \mathbb{R},\,x \ne \frac{\pi }{2} + k\pi ,\,\,k \in \mathbb{Z}} \right\}\).
\(D = \left\{ {x \in \mathbb{R},\,x \ne k\frac{\pi }{2},\,\,k \in \mathbb{Z}} \right\}\).
\(D = \left\{ {x \in \mathbb{R},\,x \ne \frac{\pi }{2} + k2\pi ,\,\,k \in \mathbb{Z}} \right\}\).
\(D = \left\{ {x \in \mathbb{R},\,x \ne k\pi ,\,\,k \in \mathbb{Z}} \right\}\).
Có bao nhiêu cách chọn 6 học sinh đổi trực nhật từ một lớp 50 học sinh?
\({6^{50}}\).
\({50^6}\).
\(C_{50}^6\).
\(A_{50}^6\).
Một đa giác lồi có 35 đường chéo. Hỏi đa giác đó có bao nhiêu đỉnh?
8.
9.
11.
10.
Trong hệ trục tọa độ Oxy, cho đường thẳng d có phương trình \(2{\rm{x}} - y + 1 = 0\), phép tịnh tiến theo vectơ \(\overrightarrow \nu \) biến d thành chính nó thì \(\overrightarrow \nu \) phải là vectơ nào trong các vectơ sau:
\(\overrightarrow \nu= \left( {2;\,\,4} \right)\).
\(\overrightarrow \nu= \left( {2;\,\, - 1} \right)\).
\(\overrightarrow \nu= \left( {4;\,\,2} \right)\).
\(\overrightarrow \nu= \left( { - 1;\,\,2} \right)\).
Hệ số của \({x^5}\) trong khai triển của biểu thức \(x{\left( {2{\rm{x}} - 1} \right)^6} + {\left( {3{\rm{x}} - 1} \right)^8}\) bằng
-13368.
13368.
-13848.
13848.
Trong hệ trục tọa độ Oxy, cho đường tròn (C) có phương trình \({\left( {x - 2} \right)^2} + {\left( {y - 2} \right)^2} = 4\). Hỏi phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số \(k = \frac{1}{2}\) và phép quay tâm O góc quay \(180^\circ \) sẽ biến đường tròn (C) thành đường tròn nào trong các đường tròn có phương trình sau:
\({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 1\).
\({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 4\).
\({\left( {x + 1} \right)^2} + {\left( {y + 1} \right)^2} = 1\).
\({\left( {x + 1} \right)^2} + {\left( {y + 1} \right)^2} = 4\).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AD và BC. Giao tuyến của hai mặt phẳng (SMN) và (SAC) là đường thẳng nào:
SD.
SO (O là tâm hình bình hành ABCD).
SG (G là trung điểm của AB).
SF (F là trung điểm của CD).
Tổng \(C_{2019}^1 + C_{2019}^2 + C_{2019}^3 + ... + C_{2019}^{1009}\) bằng:
\({2^{2018}}\).
\({2^{2018}} + 1\).
\({2^{2018}} - 1\).
\({2^{2019}}\).
Có hai xạ thủ cùng bắn vào bia. Xác suất người thứ nhất bắn trúng bia là 0,8; người thứ hai bắn trúng bia là 0,6. Xác suất để có ít nhất một người bắn trúng là:
0,95.
0,92.
0,48.
0,96.
Tìm các giá trị của tham số m để phương trình \({\sin ^6}x + {\cos ^6}x = {\cos ^2}2x + m\) có nghiệm \(x \in \left[ {0;\,\,\frac{\pi }{8}} \right]\).
\(0 \le m \le \frac{1}{8}\).
\( - \frac{1}{8} \le m \le \frac{1}{8}\).
\( - \frac{1}{8} \le m \le 0\).
Một lớp học có 30 học sinh được xếp thành một hàng dọc. Tính xác suất để hai bạn An và Hà đứng cạnh nhau?
\(\frac{1}{{30}}\).
\(\frac{1}{{28}}\).
\(\frac{2}{{15}}\).
\(\frac{1}{{15}}\).
Cho tứ diện ABCD đều cạnh a. Gọi G là trọng tâm tam giác ABC, mặt phẳng (CGD) cắt tứ diện theo một thiết diện có diện tích là:
\(\frac{{{a^2}\sqrt 2 }}{6}\).
\(\frac{{{a^2}\sqrt 3 }}{4}\).
\(\frac{{{a^2}\sqrt 2 }}{4}\).
\(\frac{{{a^2}\sqrt 3 }}{2}\).
Tập giá trị của hàm số \(y = \frac{{2\sin 2{\rm{x}} + \cos 2x}}{{\sin 2x - \cos 2x + 3}}\) có tất cả bao nhiêu giá trị nguyên?
4.
2.
3.
1.
Từ một hộp chứa 16 thẻ được đánh số từ 1 đến 16, chọn ngẫu nhiên 4 thẻ. Tính xác suất để 4 thẻ được chọn đều là số chẵn.
\(\frac{1}{{26}}\).
\(\frac{1}{{25}}\).
\(\frac{1}{{21}}\).
\(\frac{1}{{27}}\).
Cho tứ diện ABCD. Gọi M, N, P lần lượt là trung điểm của AB, BC, CD. Thiết diện của tứ diện cắt bởi mp(MNP) là hình gì trong các hình sau?
Hình thoi.
Hình vuông.
Hình chữ nhật.
Hình bình hành.
Cho hình chóp S.ABCD. Gọi M, N lần lượt là trọng tâm tam giác SAB, SAD. Gọi P là trung điểm của BC. Mệnh đề nào sau đây đúng?
\(MN//\left( {SC{\rm{D}}} \right)\).
\(MN//\left( {SB{\rm{D}}} \right)\).
\(MN//\left( {SAP} \right)\).
\(MN//\left( {S{\rm{D}}P} \right)\).
Giải các phương trình sau:
a) \(\frac{3}{{{{\sin }^2}x}} - 2\sqrt 3 \cot x - 6 = 0\)
b) \(\frac{{\cos \left( {\frac{{7\pi }}{2} - 2x} \right) - \sqrt 3 \cos \left( {2x - 3\pi } \right) + 2\cos x}}{{1 - 2\sin x}} = 0\)
a) Gọi a, b, c lần lượt là hệ số của các số hạng chứa \[{x^2}\], số hạng chứa \[{x^4}\], số hạng chứa \[{x^6}\] trong khai triển biểu thức \[{\left( {\frac{x}{2} - 4m} \right)^{12}}\] thành đa thức. Tìm m để \[a = bc\].
b) Lớp 11A có 10 học sinh nữ và một số học sinh nam. Cần chọn 5 học sinh tham gia đội văn nghệ của trường. Biết xác suất cả 5 học sinh được chọn toàn nam bằng \[\frac{7}{{15}}\] xác suất để trong 5 học sinh được chọn 2 nữ. Hỏi lớp 11A có bao nhiêu học sinh?
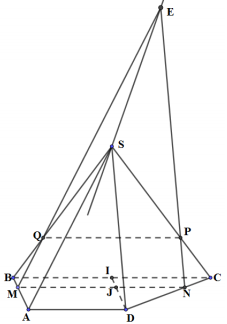
Cho hình chóp S.ABCD có đáy là hình thang ABCD với đáy lớn \(BC = 2{\rm{a}}\) và \(A{\rm{D}} = AB = a\). Mặt bên SAD là tam giác đều. Gọi M là điểm bất kì thuộc cạnh AB. Mặt phẳng \(\left( \alpha \right)\) đi qua M và song song với SA, BC, cắt CD, SC, SB lần lượt tại N, P, Q.
a) Chứng minh: \(PN//\left( {SA{\rm{D}}} \right)\).
b) Gọi E là giao điểm của MQ và NP. Chứng minh rằng E luôn nằm trên một đường thẳng cố định.
c) Giả sử \(AM = x\,\left( {0 < x < a} \right)\). Tính diện tích thiết diện tạo bởi mặt phẳng \(\left( \alpha \right)\) với hình chóp S.ABCD theo a và x. Tìm vị trí của M để thiết diện đạt giá trị lớn nhất?
Cho \(n \in {\rm N},\,\,n \ge 2\). Chứng minh rằng \(C_n^0C_n^1C_n^2...C_n^n \le {\left( {\frac{{{2^n} - 2}}{{n - 1}}} \right)^{n - 1}}\).








