Bộ 20 đề thi học kì 1 Toán 11 năm 2022 - 2023 có đáp án (Đề 10)
50 câu hỏi
Tìm dãy số là một cấp số nhân trong các dãy số dưới đây.
\(1,\,2,\, - 4,\,8\)
\( - \sqrt 2 ,\,2,\, - 2\sqrt 2 ,\,4\)
\(3,\, - \sqrt 3 ,\, - 1,\,\frac{{\sqrt 3 }}{3}\).
\(10,\,5,\,1,\,\frac{1}{5}\)
Khai triển biểu thức \(P\left( x \right) = {\left( {2x + 1} \right)^{17}}\) thu được bao nhiêu số hạng?
16
17
15
18
Tìm tập xác định \(D\) của hàm số \(y = \cot \frac{x}{2}\).
\(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,\,k \in \mathbb{Z}} \right\}\)
\(D = \mathbb{R}\backslash \left\{ {\pi + k2\pi ,\,k \in \mathbb{Z}} \right\}\)
\(D = \mathbb{R}\backslash \left\{ {k\pi ,\,k \in \mathbb{Z}} \right\}\)
\(D = \mathbb{R}\backslash \left\{ {k2\pi ,\,k \in \mathbb{Z}} \right\}\)
Xét trên tập xác định của mỗi hàm số thì khẳng định nào sau đây là đúng?
Hàm số \(y = \tan x\) là hàm số chẵn
Hàm số \(y = \sin 2x\) là hàm số lẻ
Hàm số \(y = \cot 2x\) là hàm số chẵn
Hàm số \(y = \cos x\) là hàm số lẻ
Cho dãy số \(\left( {{u_n}} \right)\) biết \({u_n} = {2^n}\). Mệnh đề nào sau đây là mệnh đề đúng?
\({u_{n + 2}} = {2^2}\)
\({u_{n + 2}} = {2.2^n}\)
\({u_{n + 2}} = {2^n} + 2\)
\({u_{n + 2}} = {4.2^n}\)
Mệnh đề nào sau đây đúng?
\(C_n^0 = n\)
\(C_n^k = C_n^{n - k}\)
\(0! = 0\)
\(1! = 1\)
Trong không gian, hai mặt phẳng tùy ý có thể có bao nhiêu vị trí tương đối nhau?
4
3
2
1
Cho 2019 điểm phân biệt nằm trên một đường tròn. Hỏi có thể lập được bao nhiêu tam giác có đỉnh là các điểm đã cho ở trên?
\({2019^3}\)
\(C_{2019}^3\)
6057
\(A_{2019}^3\)
Trong không gian cho các đường thẳng \(a,\,b\) và các mặt phẳng \(\left( \alpha \right),\,\left( \beta \right)\). Trong các khẳng định sau đây, đâu là khẳng định đúng?
Nếu \(a \cap \left( \alpha \right) = \emptyset \) thì \(a//\left( \alpha \right)\)
Nếu \(a//b\) và \(b//\left( \alpha \right)\) thì \(a//\left( \alpha \right)\)
Nếu \(a//b\) và \(b \subset \left( \alpha \right)\) thì \(a//\left( \alpha \right)\)
Nếu \(a//\left( \beta \right)\) và \(\left( \beta \right)//b\) thì \(a//b\)
Cho hàm số \(f\left( x \right) = \sin 3x\). Mệnh đề nào dưới đây sai?
Hàm số là một hàm lẻ
Hàm số có tập giá trị là \(\left[ { - 3;3} \right]\)
Hàm số có tập xác định là \(\mathbb{R}\)
Đồ thị hàm số đi qua gốc tọa độ
Gieo đồng thời hai con súc sắc (khác nhau, cân đối, đồng chất). Xác suất tổng số chấm xuất hiện trên hai súc sắc bằng 7 là
\(\frac{7}{{36}}\)
\(\frac{1}{6}\)
\(\frac{1}{4}\)
\(\frac{1}{{12}}\)
Trong không gian, đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\) nếu
\(\left\{ \begin{array}{l}a//b\\b \not\subset \left( P \right)\end{array} \right.\)
\(a \not\subset \left( P \right)\)
\(\left\{ \begin{array}{l}a//b\\b \subset \left( P \right)\\a \not\subset \left( P \right)\end{array} \right.\)
\(\left\{ \begin{array}{l}a//b\\b \subset \left( P \right)\end{array} \right.\)
Trong hệ tọa độ \(Oxy\), phép quay tâm O, góc quay \( - 90^\circ \) biến điểm \(A\left( {2;0} \right)\) thành điểm
\(Q\left( {2; - 2} \right)\)
\(T\left( {0; - 2} \right)\)
\(K\left( {0;2} \right)\)
\(H\left( { - 2;0} \right)\)
Cho lục giác đều \(ABCDEF\) có tâm \(O\). Phép tịnh tiến theo véc tơ \(\overrightarrow {BO} \) biến điểm \(O\) thành điểm nào?
Điểm \(F\)
Điểm \(D\)
Điểm \(E\)
Điểm \(B\)
Họ nghiệm của phương trình \(\sqrt 3 \sin x + \cos x = 0\) là
\(x = \frac{\pi }{6} + k\pi ,\,k \in \mathbb{Z}\)
\(x = - \frac{\pi }{3} + k\pi ,\,k \in \mathbb{Z}\)
\(x = - \frac{\pi }{6} + k\pi ,\,k \in \mathbb{Z}\)
\(x = \frac{\pi }{3} + k2\pi ,\,k \in \mathbb{Z}\)
Tìm cung lượng giác \(x\) biết rằng ba tỉ số \(1,\,2\sin x,\,\sin x + 2\) theo thứ tự lập thành một cấp số cộng.
\(x = \frac{\pi }{2} + k2\pi ,\,k \in \mathbb{Z}\)
\(x \in \emptyset \)
\(x = k\pi ,\,k \in \mathbb{Z}\)
\(x = \frac{\pi }{2} + k\pi ,\,k \in \mathbb{Z}\)
Trong một cấp số nhân gồm các số hạng dương, hiệu của số hạng thứ năm và số hạng thứ tư là 576, hiệu của số hạng thứ hai và số hạng đầu tiên là 9. Tìm tổng \({S_3}\) của 3 số hạng đầu của cấp số nhân này.
\({S_3} = 21\)
\({S_3} = - 63\)
\({S_3} = - 21\)
\({S_3} = 63\)
Khai triển biểu thức \(P\left( x \right) = {\left( {5x - 7} \right)^{99}}\) thu được \(P\left( x \right) = {a_{99}}{x^{99}} + {a_{98}}{x^{98}} + ... + {a_1}x + {a_0}\). Tính tổng \(S = {a_{99}} + {a_{98}} + ... + {a_1} + {a_0}\).
\(S = 1\)
\(S = - 1\)
\(S = {2^{99}}\)
\(S = - {2^{99}}\)
Tìm tất cả các giá trị của số thực \(m\) để phương trình \(\sin 7x = cos2m\) có nghiệm.
\(m \in \left[ { - 1;1} \right]\)
\(m \in \mathbb{R}\)
\(m \in \left[ { - \frac{1}{2};\frac{1}{2}} \right]\)
\(m \in \left[ { - \frac{1}{7};\frac{1}{7}} \right]\)
Một đội công nhân trồng cây xanh trên đoạn đường dài 5,27 kilomet. Cứ 50 mét trồng một cây. Hỏi có bao nhiêu cây được đội công nhân trồng trên đoạn đó (cây đầu tiên được trồng ở ngay đầu đoạn đường)?
107
105
106
108
Cho dãy số \(\left( {{u_n}} \right)\) có \({u_1} = 1;\,{u_{n + 1}} = {u_n} + \frac{1}{{{n^2}}},\,\forall n \in \mathbb{N}\). Trong các phát biểu sau, có bao nhiêu phát biểu đúng?
(I) \(\left( {{u_n}} \right)\) là dãy số tăng (II) \(\left( {{u_n}} \right)\) là dãy số bị chặn dưới (III) \({u_2} = 2{u_1}\)
0
1
2
3
Cho dãy số \(\left( {{u_n}} \right)\) có \({u_1} = 2,\,{u_2} = 3\) và \({u_{n + 1}} = 2{u_n} + {u_{n - 1}}\) với mọi \(n \ge 2,\,n \in \mathbb{N}\). Tìm số hạng thứ tư của dãy số đó.
\({u_4} = 19\)
\({u_4} = 13\)
\({u_4} = 14\)
\({u_4} = 17\)
Tìm tập nghiệm của phương trình \(2{\sin ^2}x + 3\sin x\cos x + 5{\cos ^2}x = 2\)
\(\left\{ { - \frac{\pi }{4} + k\pi ,\,k \in \mathbb{Z}} \right\}\)
\(\left\{ { - \frac{\pi }{4} + k2\pi ,\,k \in \mathbb{Z}} \right\}\)
\(\left\{ { - \frac{\pi }{4} + k\pi ;\,\frac{\pi }{2} + k\pi ,\,k \in \mathbb{Z}} \right\}\)
\(\left\{ { - \frac{\pi }{4} + k2\pi ;\,\frac{\pi }{2} + k\pi ,\,k \in \mathbb{Z}} \right\}\)
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành (tham khảo hình vẽ). Một mặt phẳng đồng thời song song với AC và SB lần lượt cắt các đoạn thẳng SA, AB, BC, SC, SD, BD tương ứng tại M, N, E, F, I, J. Có bao nhiêu khẳng định sai trong các khẳng định sau?
I)\(IJ//SB\)
II) \(MF//AC\)
III) Tứ giác \(MNEF\) là hình bình hành.
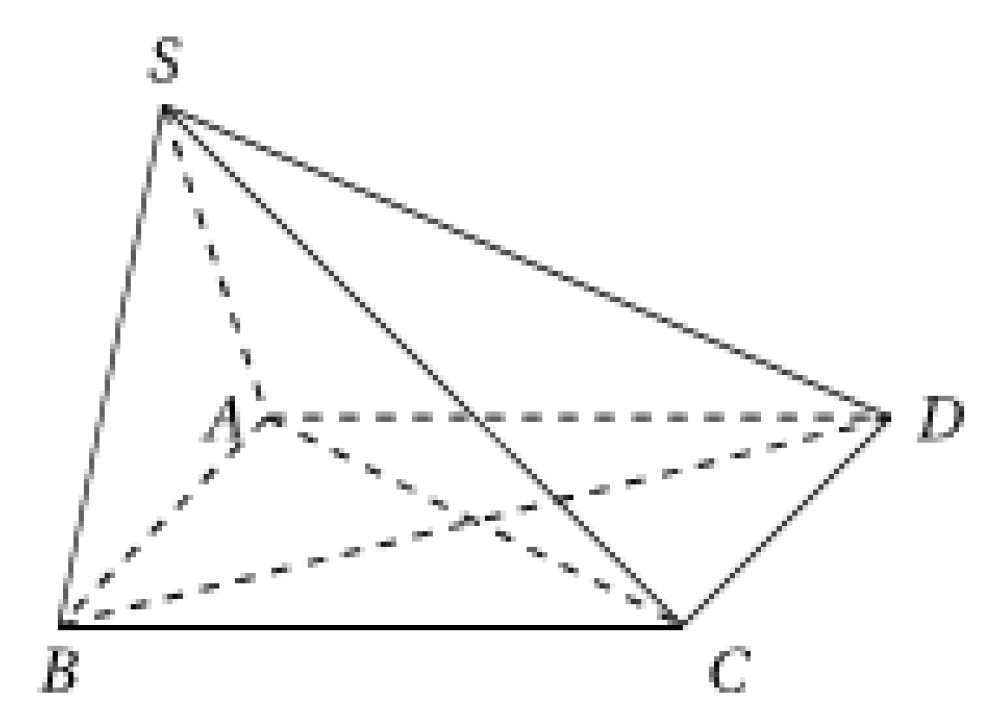
2
0
3
1
Cho cấp số cộng \(\left( {{u_n}} \right)\) thỏa mãn \(\left\{ \begin{array}{l}{u_4} = 7{u_1}\\{S_5} = 75\end{array} \right.\). Tìm số hạng thứ hai của cấp số cộng này.
\({u_2} = 12\)
\({u_2} = 9\)
\({u_2} = 6\)
\({u_2} = 3\)
Trong không gian, điều kiện nào sau đây không đủ để kết luận rằng mặt phẳng \(\left( P \right)\) song song với mặt phẳng \(\left( Q \right)\)? (giả thiết rằng các mặt phẳng đều phân biệt).
\(\left( P \right)\) và \(\left( Q \right)\) không có điểm chung
\(\left( P \right)\) chứa vô số đường thẳng song song với \(\left( Q \right)\).
\(\left( P \right)\) chứa hai đường thẳng cắt nhau và chúng cùng song song với \(\left( Q \right)\).
\(\left( P \right)\) và \(\left( Q \right)\) cùng song song với mặt phẳng \(\left( R \right)\).
Ba số thực \(a,\,b,\,c\) theo thứ tự lập thành một cấp số nhân. Tính giá trị biểu thức \(D = ac - 5b\) biết rằng \(abc = - 27\).
\(D = 24\)
\(D = - 24\)
\(D = 6\)
\(D = - 6\)
Hệ số của số hạng thứ 12 trong khai triển nhị thức \({\left( {3 - x} \right)^{15}}\) theo lũy thừa tăng dần của \(x\) là
\( - 110565\)
\( - 12285\)
\(110565\)
\(12285\)
Cho tam giác ABC có trọng tâm G. Gọi M, N, P lần lượt là trung điểm các cạnh BC, CA, AB. Phép vị tự nào sau đây biến tam giác ABC thành tam giác MNP?
Phép vị tự tâm A, tỉ số \(k = \frac{1}{2}\)
Phép vị tự tâm \(G\), tỉ số \(k = - \frac{1}{2}\)
Không có phép vị tự nào
Phép vị tự tâm \(G\), tỉ số \(k = \frac{1}{2}\)
Cho hình chóp \(S.ABCD\). Gọi G, E lần lượt là trọng tâm các tam giác SAD và SCD. Lấy M, N lần lượt là trung điểm AB, BC. Khẳng định nào sau đây đúng?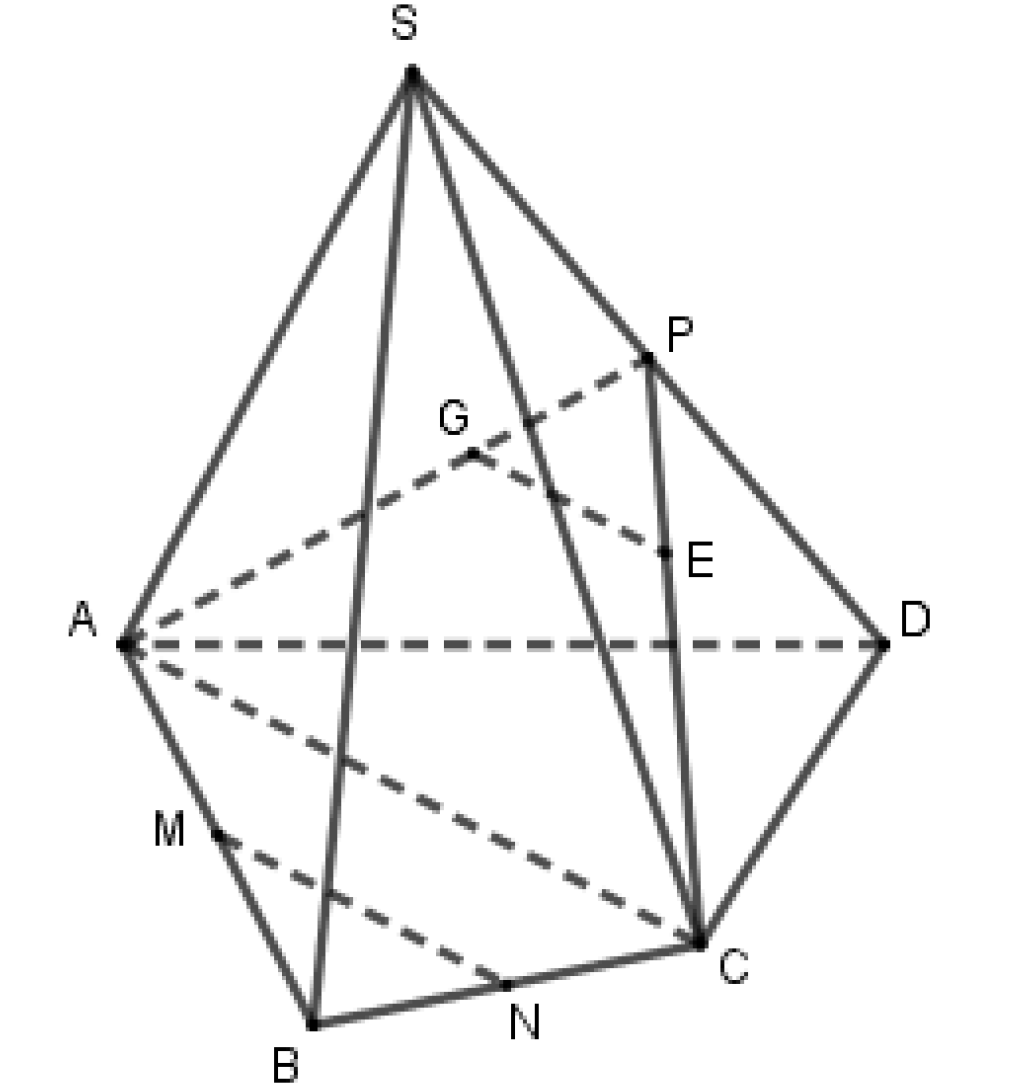
\(GE\) cắt \(BC\)
\(GE\) và \(MN\)chéo nhau
\(DE//MN\)
\(MN//SD\)
Cấp số nhân \(\left( {{u_n}} \right)\)với công bội \(q\)và số hạng đầu tiên \({u_1} > 0\)là dãy số giảm. Khẳng định nào sau đây đúng?
\(0 < q < 1\)
\(q \le 0\)
\(q > 1\)
\(\left| q \right| \le 1\)
Cho lăng trụ \(ABC.A'B'C'\) có tất cả các cạnh bằng nhau. Khi cắt lăng trụ này bởi một mặt phẳng song song với mặt phẳng (ABC) thì được thiết diện là hình gì?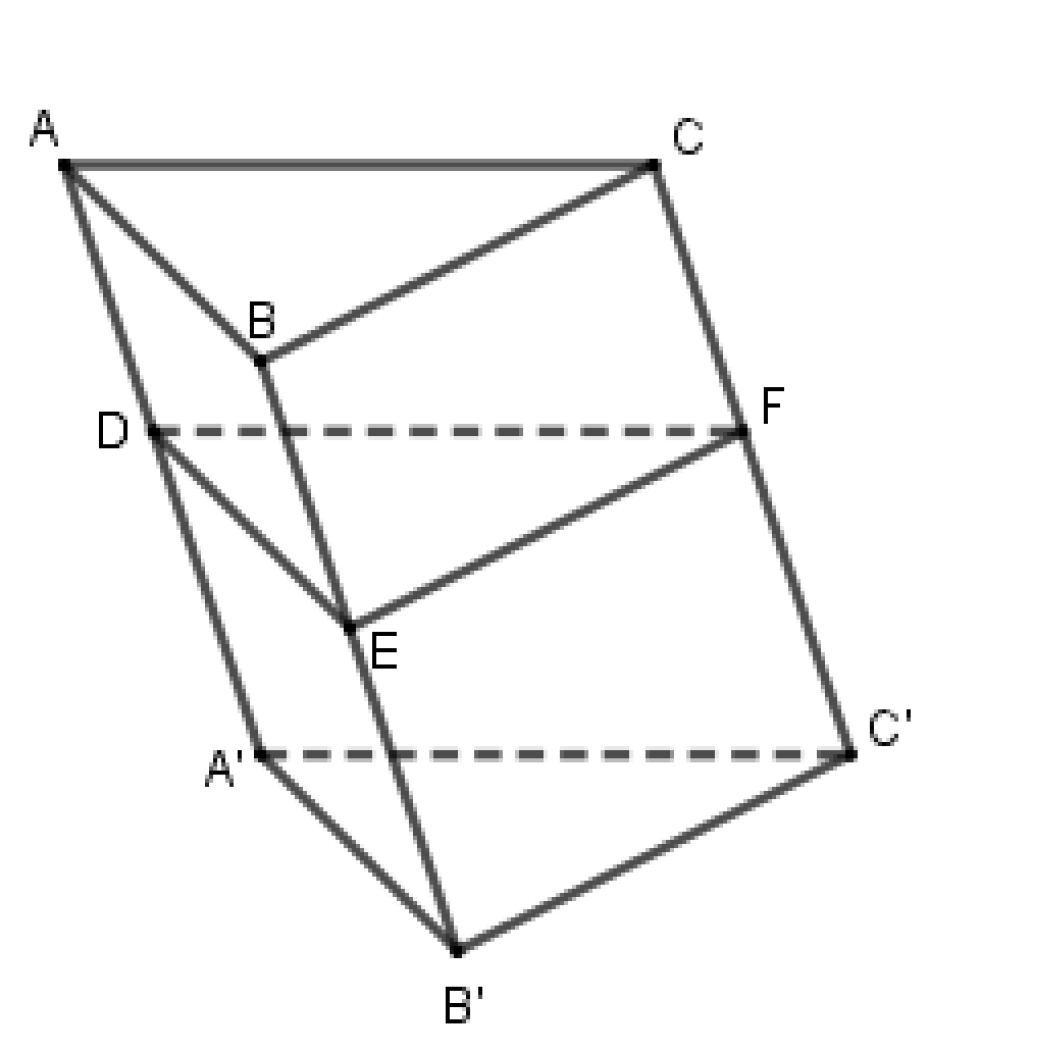
Tứ giác thường
Tam giác thường
Hình bình hành
Tam giác đều
Cho lăng trụ \(ABCD.A'B'C'D'\) có hai đáy là các hình bình hành. Các điểm M, N, P lần lượt là trung điểm của cạnh AD, BC, CC' (tham khảo hình vẽ). Xét các khẳng định sau:
I)Mặt phẳng \(\left( {MNP} \right)\) cắt cạnh \(A'D'\)
II) Mặt phẳng \(\left( {MNP} \right)\) cắt cạnh \(DD'\) tại trung điểm của \(DD'\)
III) Mặt phẳng \(\left( {MNP} \right)\) song song với mặt phẳng \(\left( {ABC'D'} \right)\)
Trong các khẳng định trên, số khẳng định đúng là
3
1
4
2
Có bao nhiêu số tự nhiên có ba chữ số được lập thành từ các chữ số 0, 2, 4, 6, 8, 9?
120
180
100
256
Trong các mệnh đề sau, có bao nhiêu mệnh đề đúng?
I) Hàm số \(y = x + {\mathop{\rm sinx}\nolimits} \) tuần hoàn với chu kì \(T = 2\pi \)
II) Hàm số \(y = x\cos x\) là hàm số lẻ
III) Hàm số \(y = \tan x\) đồng biến trên từng khoảng xác định
2
1
3
0
Cho cấp số nhân \(\left( {{u_n}} \right)\) có \({u_5} = 15\) và \({u_{18}} = - 1875\). Công bội của cấp số nhân là
\(q = 3\)
\(q = 5\)
\(q = - 5\)
\(q = - 3\)
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành, M là điểm bất kì năm trong đoạn thẳng \(SC\). Mặt phẳng \(\left( \alpha \right)\) đi qua \(M\) và song song với mặt phẳng \(\left( {SAB} \right)\). Thiết diện của hình chóp \(S.ABCD\)cắt bởi mặt phẳng \(\left( \alpha \right)\) là hình gì?
Hình bình hành
Hình thang
Hình tam giác cân
Hình ngũ giác
Giải bóng đá Vô địch quốc gia Việt Nam 2018 (Nuti Café V.League 2018) có 14 đội bóng tham dự theo thể thức vòng tròn tính điểm lượt đi - lượt về (nghĩa là 2 đội bất kì sẽ đấu với nhau đúng 2 trận). Hỏi có tất cả bao nhiêu trận đấu diễn ra trong cả giải đấu đó?
196 trận
182 trận
98 trận
91 trận
Cho chóp tứ giác \(S.ABCD\) có đáy là hình bình hành (tham khảo hình vẽ). Gọi I, J, K lần lượt là trung điểm các cạnh SA, SB, SC. Mệnh đề nào sau đây là mệnh đề sai?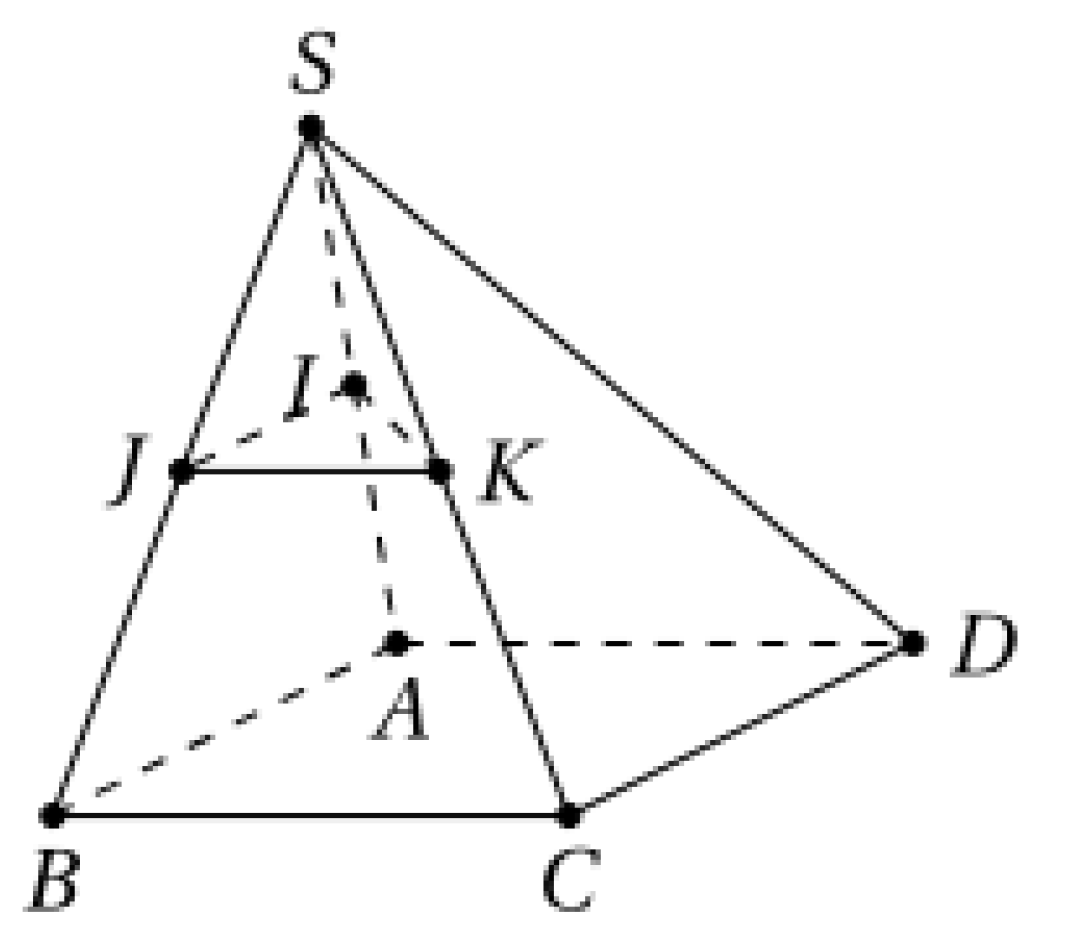
\(IJ//CD\)
\(SD \cap \left( {IJK} \right) = \emptyset \)
\(\left( {IJK} \right) \cap \left( {ACD} \right) = \emptyset \)
\(IK//AC\)
Có bao nhiêu cách xếp ba bạn nam và hai bạn nữ thành một hàng ngang sao cho hai bạn nữ không đứng cạnh nhau?
36
24
72
120
Trong một hộp có 9 tấm thẻ được đánh số từ 1 đến 9. Lấy ngẫu nhiên ra bốn thẻ và xếp cạnh nhau theo thứ tự từ trái sang phải. Tính xác suất để bốn thẻ đó xếp thành một số tự nhiên chẵn.
\(\frac{2}{3}\)
\(\frac{4}{9}\)
\(\frac{5}{9}\)
\(\frac{1}{3}\)
Cho hình hộp \(ABCD.A'B'C'D'\) (tham khảo hình vẽ). Hai điểm \(M,\,N\) lần lượt nằm trên hai cạnh \(AD,\,CC'\) sao cho \(AM = \frac{1}{2}AD,\,CN = \frac{1}{4}CC'\). Thiết diện của hình hộp cắt bởi mặt phẳng chứa đường thẳng \(MN\) và song song với mặt phẳng \(\left( {ACB'} \right)\) là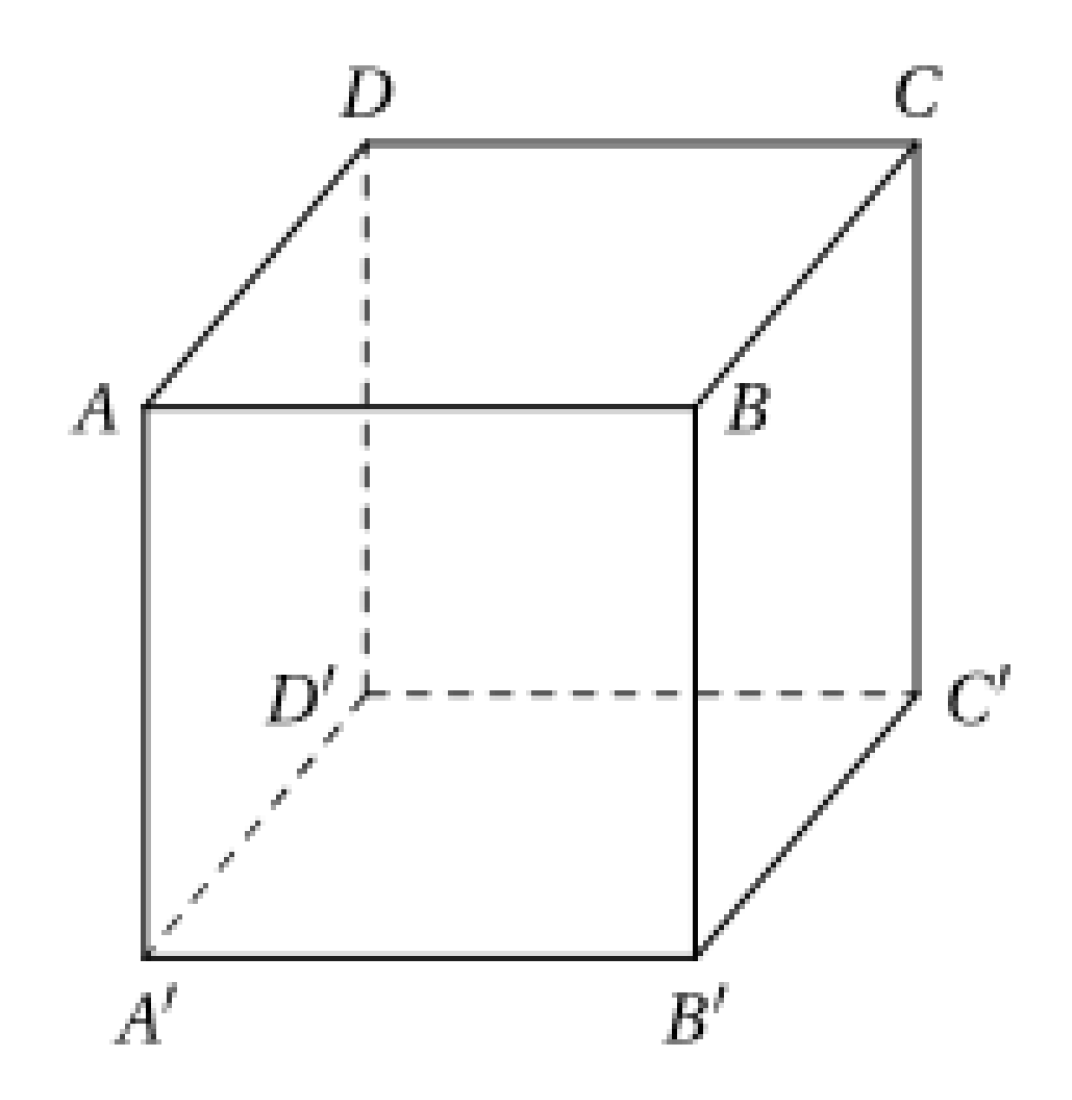
hình lục giác
hình ngũ giác
hình tam giác
không có thiết diện
Cho hình hộp \(ABCD.A'B'C'D'\) (tham khảo hình vẽ). Gọi \(M\) là trung điểm cạnh \(A'D'\) và \(\left( \alpha \right)\) là mặt phẳng đi qua \(M\), song song với các đường thẳng \(BB',\,AC\). Gọi \(T\) là giao điểm của đường thẳng \(BC\) và mặt phẳng \(\left( \alpha \right)\). Tính tỉ số \(\frac{{TB}}{{TC}}\).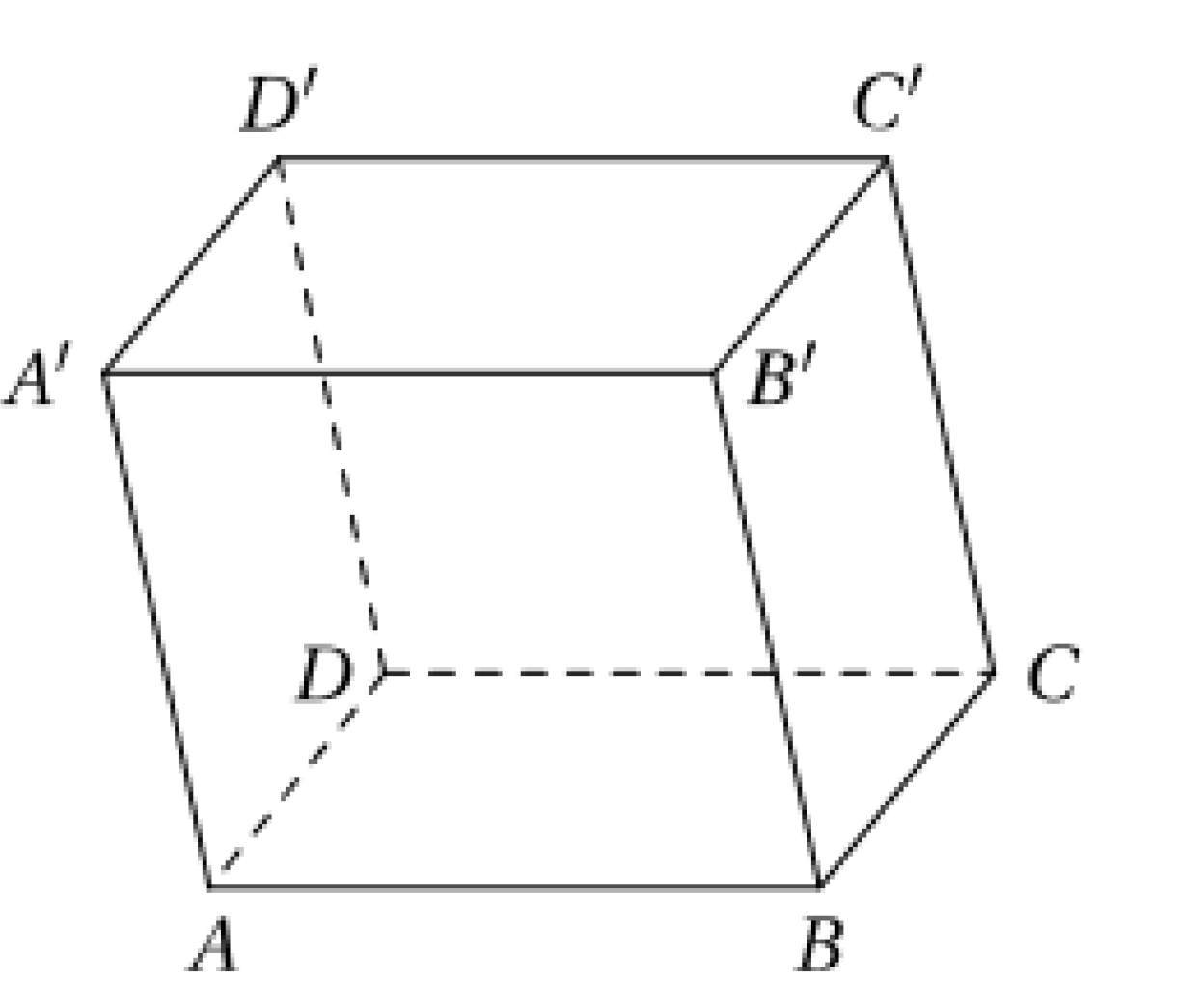
2
\(\frac{2}{3}\)
3
\(\frac{3}{2}\)
Một túi đựng 9 quả cầu màu xanh, 3 quả cầu màu đỏ, 7 quả cầu màu vàng. Lấy ngẫu nhiên 6 quả cầu trong túi. Tính xác suất sao cho lấy được cả ba loại cầu, đồng thời số quả cầu màu xanh bằng số quả cầu màu đỏ.
\(\frac{{165}}{{1292}}\)
\(\frac{9}{{76}}\)
\(\frac{{118}}{{969}}\)
\(\frac{{157}}{{1292}}\)
Cho tứ diện \(ABCD\) có \(BC = 9,\,AC = 6\) và \(BD = 3\) (tham khảo hình vẽ). Điểm \(M\) di chuyển trên cạnh \(BC\). Mặt phẳng \(\left( \alpha \right)\) qua \(M\), song song với \(AC\) và \(BD\) cắt tứ diện theo thiết diện là một tứ giác. Khi \(M\) di chuyển đến vị trí \({M_0}\) để thiết diện đó là một hình thoi, hãy tính tích \({M_0}B.{M_0}C\)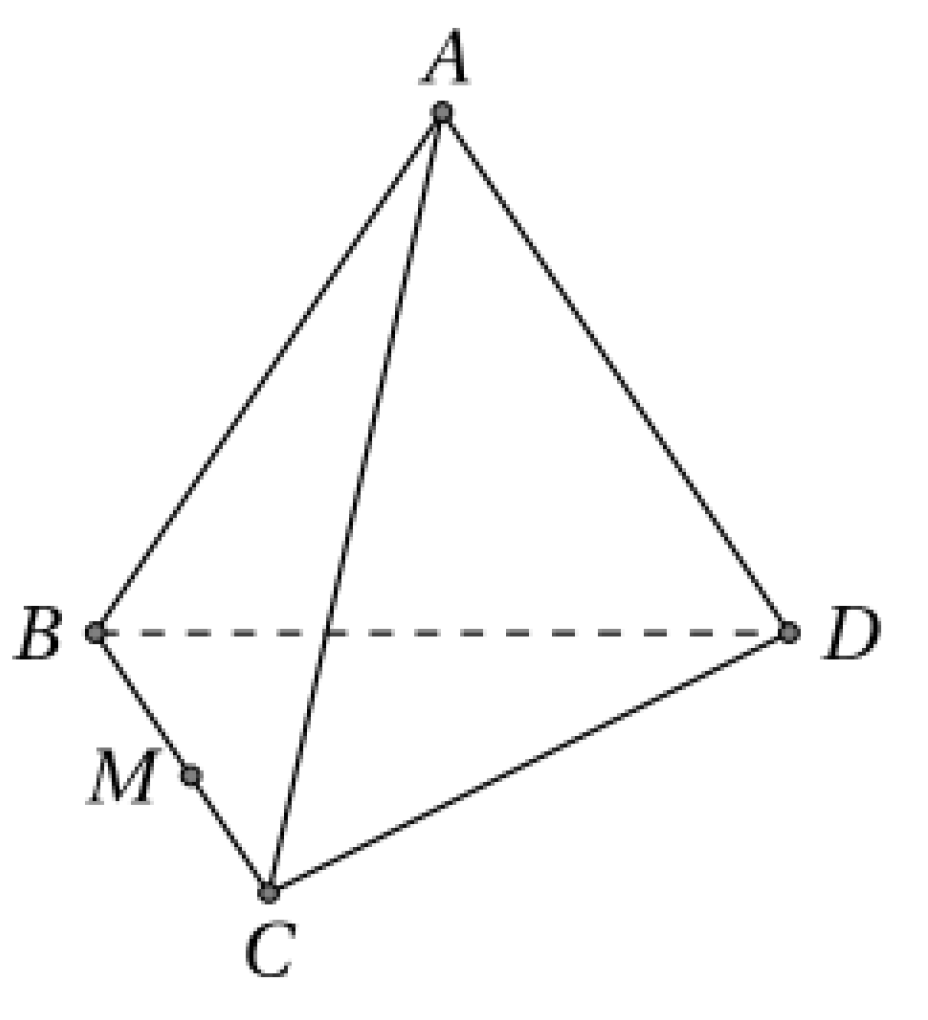
\(\frac{{81}}{4}\)
14
18
20
Cho dãy số \(\left( {{u_n}} \right)\) thỏa mãn \({u_1} = 6\) và \({u_{n + 1}} = \frac{1}{9}\left( {u_n^2 - {u_n} + 25} \right)\) với mọi số tự nhiên \(n \ge 1\). Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
I) \(\left( {{u_n}} \right)\) là dãy số không tăng, không giảm.
II) \(\frac{1}{{{u_1} + 4}} = \frac{1}{{{u_1} - 5}} - \frac{1}{{{u_2} - 5}}\)
III) \(\frac{1}{{{u_1} + 4}} + \frac{1}{{{u_2} + 4}} + ... + \frac{1}{{{u_{2018}} + 4}} = 1 - \frac{1}{{{u_{2019}} - 5}}\)
3
2
1
0
Số tự nhiên \(n\) thỏa mãn đẳng thức \(1 + 4 + 7 + ... + \left( {3n + 1} \right) = 4187\) là
52
51
50
49
Một lớp học có 3 tổ. Tổ I gồm có 3 học sinh nam và 7 học sinh nữ; tổ II gồm có 5 học sinh nam và 5 học sinh nữ; tổ III gồm 6 học sinh nam và 4 học sinh nữ. Cô giáo chủ nhiệm cần chọn ra một học sinh nam và một học sinh nữ để tham gia hoạt động tình nguyện. Hỏi cô giáo có bao nhiêu cách chọn, nếu cô muốn chọn hai em học sinh ở hai tổ khác nhau?
154
145
242
224
Trong một trò chơi, người chơi cần gieo cùng lúc ba con súc sắc cân đối, đồng chất; nếu được ít nhất hai con súc sắc xuất hiện mặt có số chấm lớn hơn 4 thì người chơi đó thắng. Tính xác suất để trong ba lần chơi, người chơi thắng ít nhất một lần.
\(\frac{{11683}}{{19683}}\)
\(\frac{2}{9}\)
\(\frac{{386}}{{729}}\)
\(\frac{7}{{27}}\)
Tập nghiệm của phương trình \(\cos 2x - \sin x = 0\) được biểu diễn bởi tất cả bao nhiêu điểm trên đường tròn lượng giác?
3 điểm
4 điểm
2 điểm
1 điểm








