12 câu hỏi
A. TRẮC NGHIỆM (7,0 điểm)
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Số hữu tỉ là số được viết dưới dạng phân số \(\frac{a}{b}\) với
\(a,b \in \mathbb{N},a \ne 0.\)
\(a,b \in \mathbb{Z},b \ne 0.\)
\(a,b \in \mathbb{N},b \ne 0.\)
\(a = 0,b \ne 0.\)
Cho trục số sau.

Điểm \(B\) biểu diễn số hữu tỉ nào?
\(\frac{7}{5}.\)
\( - \frac{2}{5}.\)
\(\frac{9}{5}.\)
\(\frac{3}{5}.\)
Ta có \({x^{14}}\) là kết quả của phép toán
\({x^{14}}.x.\)
\({x^7}.{x^2}\).
\({x^{10}}.{x^4}.\)
\({x^{13}}:x.\)
Tính \({\left( { - \frac{1}{2}} \right)^4}\) bằng
\(\frac{1}{{16}}.\)
\( - \frac{1}{{16}}.\)
\(\frac{1}{8}.\)
\( - \frac{1}{8}.\)
Đối với biểu thức có chứa dấu ngoặc thì thứ tự thực hiện phép tính trên tập số hữu tỉ nào dưới đây là đúng?
\(\left( {} \right) \to \left[ {} \right] \to \left\{ {} \right\}.\)
\(\left[ {} \right] \to \left( {} \right) \to \left\{ {} \right\}.\)
\(\left\{ {} \right\} \to \left[ {} \right] \to \left( {} \right).\)
\(\left( {} \right) \to \left\{ {} \right\} \to \left[ {} \right].\)
Số thập phân \(0,15\) biểu diễn số hữu tỉ nào dưới đây?
\(\frac{3}{{20}}.\)
\(\frac{1}{{15}}.\)
\(\frac{2}{{15}}.\)
\(\frac{4}{{15}}.\)
Trong các khẳng định sau, khẳng định nào đúng?
Số vô tỉ không phải là số thập phân vô hạn tuần hoàn.
Số vô tỉ là số được viết dưới dạng số thập phân vô hạn không tuần hoàn.
Số vô tỉ cũng là số thập phân hữu hạn.
Số vô tỉ là số thập phân vô hạn tuần hoàn.
Cho số \(a \ge 0\), đẳng thức nào sau đây là đúng?
\({\left( {\sqrt a } \right)^2} = {a^2}.\)
\({\left( {\sqrt a } \right)^2} = a.\)
\({\left( {\sqrt a } \right)^2} = 2a.\)
\({\left( {\sqrt a } \right)^2} = 2\sqrt a .\)
Số đỉnh của hình hộp chữ nhật là
\(10.\)
\(12.\)
\(8.\)
\(4.\)
Trong các hình sau, hình nào là lăng trụ đứng tam giác?
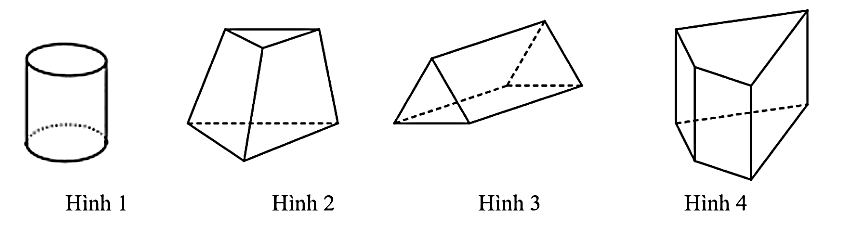
Hình 1.
Hình 2.
Hình 3.
Hình 4.
Hai góc được đánh dấu trong hình nào dưới đây là hai góc kề bù?

Hình 1.
Hình 2.
Hình 3.
Hình 4.
Cho tia \(At\) là tia phân giác của góc \(xAy\) thì ta có
\(\widehat {xAt} = 2\widehat {yAt}.\)
\(\widehat {xAt} + \widehat {yAt} = 180^\circ .\)
\(\widehat {xAt} - \widehat {yAt} = 180^\circ .\)
\(\widehat {xAt} = \widehat {yAt}.\)
