12 câu hỏi
Khẳng định nào sau đây là đúng?
\(\frac{5}{9} \in \mathbb{Q}.\)
\(\frac{1}{3} \in \mathbb{Z}.\)
\(\frac{{ - 8}}{5} \notin \mathbb{Q}.\)
\( - 11 \in \mathbb{N}.\)
Cho hai số hữu tỉ \(a\) và \(b\) được biểu diễn trên trục số như sau.
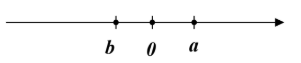
Chọn khẳng định đúng.
\(b > 0 > a.\)
\(b > a.\)
\(b < a < 0.\)
\(b < 0 < a.\)
Biểu thức \({\left( { - \frac{2}{5}} \right)^3}\) bằng
\(\frac{4}{{25}}.\)
\(\frac{{ - 4}}{{25}}.\)
\(\frac{8}{{125}}.\)
\(\frac{{ - 8}}{{125}}.\)
Thực hiện bỏ ngoặc biểu thức \(a - \left( {a + c} \right) + \left( {b + c} \right)\) ta được
\(b - c.\)
\(b + c.\)
\(b + 2c.\)
\(b.\)
Tập hợp các số vô tỉ được kí hiệu là
\(\mathbb{N}.\)
\(\mathbb{Z}.\)
𝕀.
\(\mathbb{Q}.\)
Số 9 là căn bậc hai số học của số
\(81.\)
\( - 81.\)
\(3.\)
\( - 3.\)
Công thức tính diện tích xung quanh của hình hộp chữ nhật có chiều dài là \(a,\) chiều rộng là \(b,\) chiều cao là \(h\) (\(a,b,h\) cùng đơn vị đo) là
\({S_{xq}} = 2\left( {a + b} \right).h.\)
\({S_{xq}} = 2a.b.h.\)
\({S_{xq}} = \left( {a + b} \right).h.\)
\({S_{xq}} = a.b.h.\)
Trong các hình triển khai dưới đây, có bao nhiêu hình gấp lại được thành một hình lăng trụ đứng tam giác?
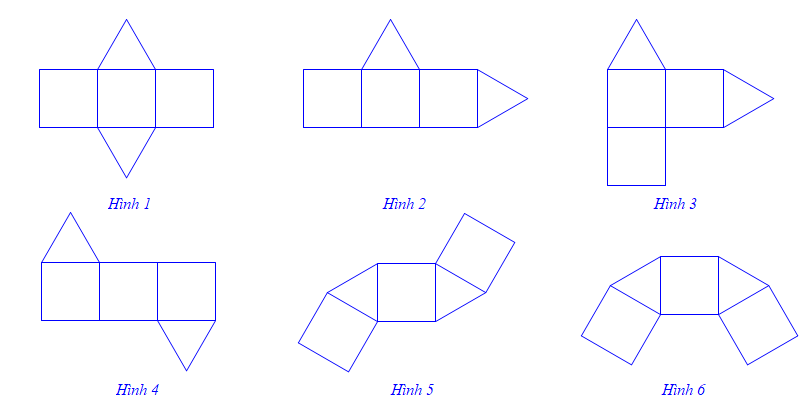
2.
3.
4.
5.
Trong các hình sau, hình nào có dạng hình lập phương?

Hình 1.
Hình 2.
Hình 3.
Hình 4.
Chọn phát biểu sai. Hình lăng trụ đứng tứ giác có
Các mặt đáy song song với nhau.
Các mặt đáy đều là hình tam giác.
Các mặt bên đều là hình chữ nhật.
Các mặt đáy đều là hình tứ giác.
Hai đường thẳng \(zz'\) và \(tt'\) cắt nhau tại \(A\). Góc đối đỉnh của \(\widehat {zAt'}\) là
\(\widehat {z'At'}.\)
\(\widehat {z'At}.\)
\(\widehat {zAt'}.\)
\(\widehat {zAt}.\)
Khẳng định nào sau đây là đúng?
Hai góc kề bù có tổng số đo bằng \(180^\circ .\)
Hai góc có tổng bằng \(180^\circ \) thì kề bù.
Hai góc kề bù có tổng bằng \(90^\circ .\)
Hai góc có tổng bằng \(180^\circ \) thì kề nhau.
