12 bài tập Sử dụng dấu của đạo hàm để tìm điểm cực trị của hàm số có lời giải
12 câu hỏi
Cho hàm số y = f(x) liên tục trên ℝ và có bảng xét dấu đạo hàm dưới đây
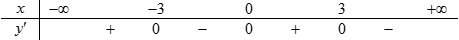 .
.
Số điểm cực trị của hàm số là
1;
2;
3;
4.
Cho hàm số y = f(x) liên tục trên ℝ và có bảng xét dấu f'(x) như sau:

Kết luận nào sau đây đúng
Hàm số có 4 điểm cực trị;
Hàm số có 2 điểm cực đại;
Hàm số có 1 điểm cực trị;
Hàm số có 2 điểm cực tiểu.
Hàm số \[y = \frac{{2x + 3}}{{x + 1}}\] có bao nhiêu điểm cực trị?
3;
2;
0;
1.
Cho hàm số y = f(x) liên tục trên ℝ và có f'(x) = (x – 1)2(x2 – 5x + 6). Số điểm cực trị của hàm số đã cho là
5;
3;
2;
4.
Cho hàm số f(x) có đạo hàm f'(x) = x – 1, ∀x ∈ ℝ . Hỏi f(x) có bao nhiêu điểm cực trị?
0;
1;
2;
3.
Cho hàm số y = f(x) có bảng xét dấu của đạo hàm như hình bên. Số điểm cực tiểu của hàm số y = f(x) là
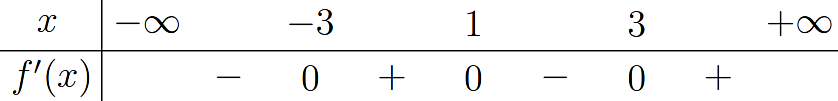
3;
4;
2;
1.
Cho hàm số y = f(x) liên tục trên ℝ và có bảng xét dấu của đạo hàm như hình vẽ.
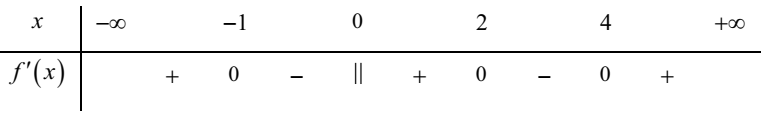
Hàm số y = f(x) có bao nhiêu điểm cực trị?
1;
2;
3;
4.
Cho hàm số y = f(x) có đạo hàm f'(x) = (1 - x)2(x + 1)3(3 – x), ∀x ∈ ℝ. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
(−∞; 1);
(−∞; −1);
(−1; 3);
(3; +∞).
Cho hàm số y = f(x) liên tục trên ℝ và có bảng xét dấu của f'(x) như sau:
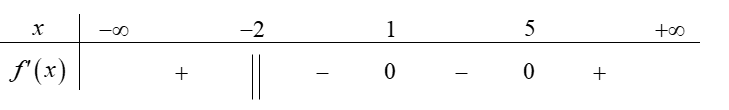
Tìm số điểm cực trị của hàm số đã cho.
1;
2;
3;
0.
Cho hàm số f(x) có bảng xét dấu đạo hàm như sau:
![]()
Hàm số y = f(x) có bao nhiêu điểm cực trị.
Cho hàm số f(x) có bảng xét dấu của f'(x) như hình vẽ
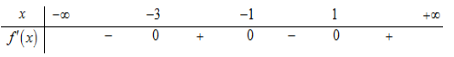
Tìm điểm cực đại của hàm số.
Hàm số nào trong bốn hàm số được liệt kê dưới đây không có cực trị?
y = −x3 + x;
y = x4;
\(y = \frac{{2x - 1}}{{x + 1}}\);
y = |x|.