10 bài tập Xác định vectơ, chỉ ra các yếu tố của vectơ có lời giải
10 câu hỏi
Trong các vectơ sau, vectơ nào sau đây có điểm đầu là A, điểm cuối là B?
\(\overrightarrow {AA} \);
\(\overrightarrow {BA} \);
\(\overrightarrow {AB} \);
\(\overrightarrow {BB} \).
Trong không gian cho 3 điểm phân biệt A, B, C. Vectơ nào trong các vectơ sau đây là vectơ – không?
\(\overrightarrow {BB} \);
\(\overrightarrow {BA} \);
\(\overrightarrow {BC} \);
\(\overrightarrow {CA} \).
Cho hình hộp chữ nhật ABCD.A'B'C'D'.
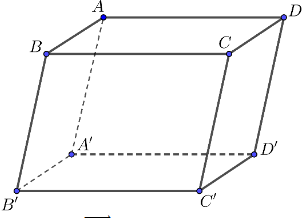
Vectơ nào sau đây cùng phương với \(\overrightarrow {BC} \).
\(\overrightarrow {DC} \);
\(\overrightarrow {DA} \);
\(\overrightarrow {BB'} \);
\(\overrightarrow {C'C} \).
Cho hình hộp chữ nhật ABCD.A'B'C'D'.

Vectơ \(\overrightarrow {BA} \) bằng với vectơ nào sau đây?
\(\overrightarrow {A'B'} \);
\(\overrightarrow {CD} \);
\(\overrightarrow {BC} \);
\(\overrightarrow {AB} \).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, vectơ nào sau đây bằng vectơ \(\overrightarrow {AB} \)?
\(\overrightarrow {DC} \);
\(\overrightarrow {CD} \);
\(\overrightarrow {AD} \);
\(\overrightarrow {BC} \).
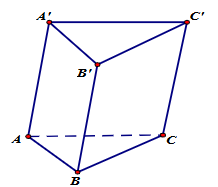
Cho hình lăng trụ ABC.A'B'C'. Số vectơ khác vectơ – không bằng vectơ \(\overrightarrow {AA'} \) có điểm đầu và điểm cuối là các đỉnh của hình lăng trụ là
1;
2;
3;
4.
Cho tứ diện ABCD, gọi I là trung điểm của đoạn thẳng AB. Vectơ \(\overrightarrow {AI} \) cùng hướng với vectơ nào sau đây?
\(\overrightarrow {BI} \);
\(\overrightarrow {CD} \);
\(\overrightarrow {CI} \);
\(\overrightarrow {AB} \).
Cho tứ diện ABCD. Hỏi có bao nhiêu vectơ khác vectơ \(\overrightarrow 0 \) mà mỗi vectơ có điểm đầu, điểm cuối là hai đỉnh của tứ diện ABCD?
12;
4;
10;
8.
Trong không gian, cho hình hộp ABCD.A'B'C'D'. Vectơ đối của vectơ \(\overrightarrow {AA'} \) là:
\(\overrightarrow {A'C'} \);
\(\overrightarrow {BA'} \);
\(\overrightarrow {BB'} \);
\(\overrightarrow {C'C} \).
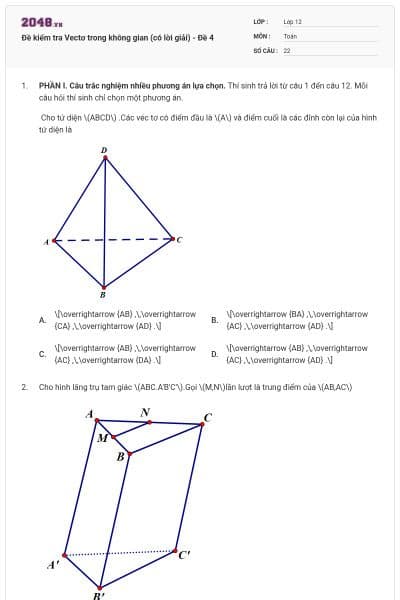
Cho tứ diện ABCD. Các vectơ có điểm đầu là A và điểm cuối là các đỉnh còn lại của hình tứ diện là
\(\overrightarrow {AB} ;\overrightarrow {CA} ;\overrightarrow {AD} \);
\(\overrightarrow {BA} ;\overrightarrow {AC} ;\overrightarrow {AD} \);
\(\overrightarrow {AB} ;\overrightarrow {AC} ;\overrightarrow {DA} \);
\(\overrightarrow {AB} ;\overrightarrow {AC} ;\overrightarrow {AD} \).