(Trả lời ngắn) 30 bài tập Vectơ và các phép toán trong không gian (có lời giải)

Cho hình lâp phương \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) có cạnh bằng \(a\). Gọi \(M,N\) lần lượt là trung điểm của  \({A^\prime }{D^\prime }\) và \({C^\prime }{D^\prime }\). Tích vô hướng \(\overrightarrow {MN}  \cdot \overrightarrow {{C^\prime }B}  = n{a^2}\) ( \(n\) là số thập phân). Giá trị của \(n\) bằng bao nhiêu?

Cho hình lập phương \(ABCD \cdot A'B'C'D'\left( {H.2.6} \right)\). Trong các vectơ \(\overrightarrow {AC} ,\overrightarrow {AD} ,\overrightarrow {AD'} \) :a) Hai vectơ nào có giá cùng nằm trong mặt phẳng \(\left( {{\rm{ABCD}}} \right)\) ?b) Hai vectơ nào có cùng độ dài?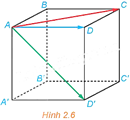

Cho hình lăng trụ tam giác đều \(ABC \cdot A'B'C'\left( {H.2.25} \right)\). Tính các góc \(\left( {\overrightarrow {AA'} ,\overrightarrow {BC} } \right)\) và \(\left( {\overrightarrow {AB} ,\overrightarrow {A'C'} } \right)\).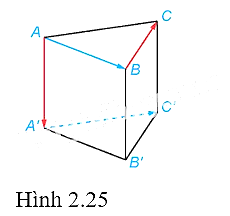

Cho hình lập phương ABCD.A'B'C'D'. Tính $\underset{A\text{'}C}{\to }.\underset{B\text{'}D\text{'}}{\to }$

Như đã biết, nếu có một lực \(\vec F\) tác động vào một vật tại điểm \(M\) và làm cho vật đó di chuyển một quãng đường \({\rm{MN}}\) thì công \({\rm{A}}\) sinh ra được tính theo công thức \(A = \vec F \cdot \overrightarrow {MN} \), trong đó lực \({\rm{F}}\) có độ lớn tính bằng Newton, quãng đường \(MN\) tính bằng mét và công \(A\) tính bằng Jun (H.2.28). Do đó, nếu dùng một lực \(\vec F\) có độ lớn không đổi để lâm một vật di chuyển một quãng đường không đối thì công sinh ra sê lớn nhất khi lực tác đônng cưng hướng với chuyển động của vật. Hây giải thích vì sao. Kết quả trên có thể được áp dụng như thể nảo khi kêo (hoặc đầy) các vật nặng?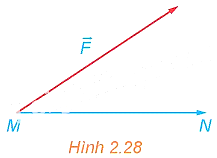

Cho tứ diện \(ABCD\). Tính  \(\overrightarrow {AB}  \cdot \overrightarrow {CD}  + \overrightarrow {AC}  \cdot \overrightarrow {DB}  + \overrightarrow {AD}  \cdot \overrightarrow {BC} \)

Trong không gian, cho hai vectơ \(\vec a\) và \(\vec b\) có cùng độ dài bằng 1. Biết rằng góc giữa hai vectơ đó là \({45^ \circ }\), hãy tính:

a) \(\vec a \cdot \vec b\)

b) \(\left( {\vec a + 3\vec b} \right) \cdot \left( {\vec a - 2\vec b} \right)\)

c) \({(\vec a + \vec b)^2}\).

Cho hình lăng trụ tứ giác đều \(ABCD \cdot A'B'C'D'\) có độ dài mỗi cạnh đáy bằng 1 và độ dài mỗi cạnh bên bằng 2 . Hãy tính góc giữa các cặp vectơ sau đây và tính tích vố hướng của mối cập vectơ đó:
a) \(\overrightarrow {AA'} \) và \(\overrightarrow {C'C} \)b) \(\overrightarrow {AA'} \) và \(\overrightarrow {BC} \) c) \(\overrightarrow {AC} \) và \(\overrightarrow {B'A'} \).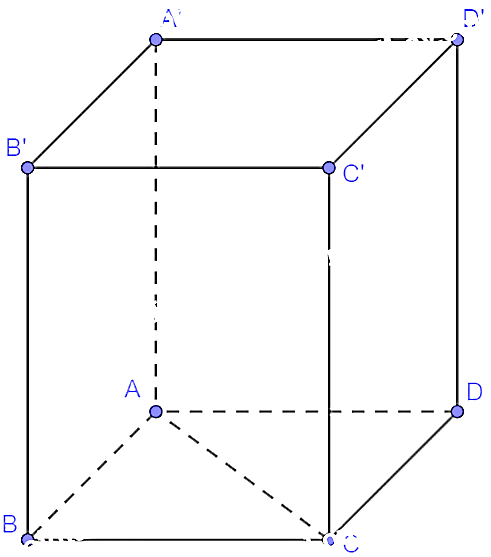

Cho hình chóp \({\rm{S}}.{\rm{ABC}}\). Trên cạnh \({\rm{SA}}\), lấy điểm \({\rm{M}}\) sao cho \(SM = 2AM\). Trên cạnh \({\rm{BC}}\), lấy điểm \({\rm{N}}\) sao cho \(CN = 2BN\). Tính \(\left( {\overrightarrow {SA}  + \overrightarrow {BC} } \right) + \overrightarrow {AB} \).

Cho hình chóp tứ giác \({\rm{S}} \cdot {\rm{ABCD}}\). Nếu \(\overrightarrow {SA}  + \overrightarrow {SC}  = \overrightarrow {SB}  + \overrightarrow {SD} \) thì ABCD là hình gì?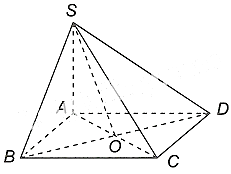

Cho hình lăng trụ tam giác \(ABC \cdot A'B'C'\) có \(\overrightarrow {AA'}  = \vec a,\overrightarrow {AB}  = \vec b\) và \(\overrightarrow {AC}  = \vec c\). Hãy biểu diễn các vectơ sau qua các vecto \(\vec a,\vec b,\vec c\) :

a) \(\overrightarrow {AB'} \);

b) \(\overrightarrow {B'C} \)

c) \(\overrightarrow {BC'} \).

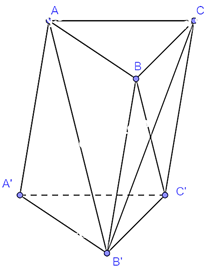
Cho hình hộp chữ nhật \(ABCD \cdot A'B'C'D'\) có \(AB = 2,AD = 3\) và \(AA' = 4\). Tính độ dài của các vectơ \(\overrightarrow {BB'} ,\overrightarrow {BD} \) và \(\overrightarrow {BD'} \).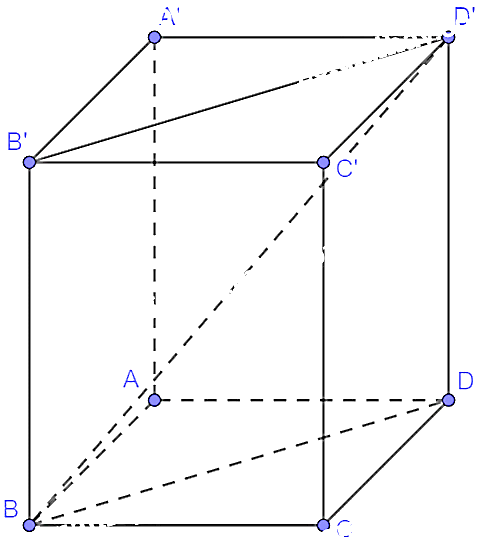

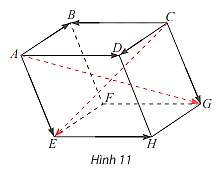
Cho hình lăng trụ \(ABC \cdot A'B'C'\). Tìm các vectơ tổng \(\overrightarrow {BA}  + \overrightarrow {A'C'} ,\overrightarrow {BC}  + \overrightarrow {AA'} \).

Cho hình hộp \(ABCD.EFGH\). Thực hiện các phép toán sau đây:

a) \(\overrightarrow {CB}  + \overrightarrow {CD}  + \overrightarrow {CG} \);

b) \(\overrightarrow {AB}  + \overrightarrow {CG}  + \overrightarrow {EH} \).

Có ba lực cùng tác động vào một vật. Hai trong ba lực này hợp với nhau một góc \({100^ \circ }\) và có độ lớn lần lượt là \(25{\rm{\;N}}\) và \(12{\rm{\;N}}\). Lực thứ ba vuông góc với mặt phẳng tạo bởi hai lực đã cho và có độ lớn \(4{\rm{\;N}}\). Tính độ lớn của hợp lực của ba lực trên.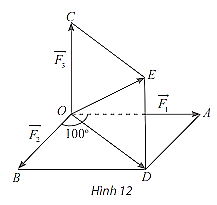

Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Tìm các vectơ hiệu \(\overrightarrow {SD}  - \overrightarrow {SA} ,\overrightarrow {BS}  - \overrightarrow {AD} \).

Cho hình hộp \(ABCD \cdot A'B'C'D'\). Tìm vectơ \(\overrightarrow {CC'}  + \overrightarrow {BA}  + \overrightarrow {D'A'} \).

Cho hình lập phương \(ABCD \cdot A'B'C'D'\). Xác định góc \(\left( {\overrightarrow {AB} ,\overrightarrow {A'D'} } \right),\left( {\overrightarrow {AB} ,\overrightarrow {A'C'} } \right)\).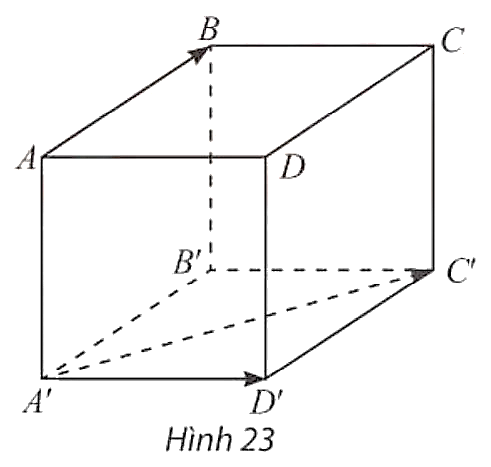

Cho tứ diện \(ABCD\). G là trọng tâm của tam giác \(BCD\) (Hình 2.15). Tính \(\overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD} \)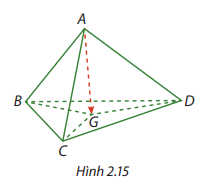

Cho hình hộp ABCD.EFGH. Điểm \(M\) là trọng tâm tam giác \(AFH\) (Hình 2.16). Tính độ dài của \(\overrightarrow {EM} \) trong trường hợp \(ABCD\).EFGH là hình hộp đứng có các cạnh \(AB = 5,AD = 6,AE = 10\) và \(\widehat {ABC} = {120^ \circ }\).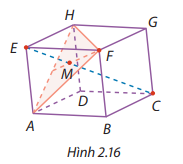

Cho tứ diện đều \(ABCD\) có cạnh bằng \(a\) và \(M\) là trung điểm của \(CD\).

a) Tính các tích vô hướng \(\overrightarrow {AB}  \cdot \overrightarrow {AC} ,\overrightarrow {AB}  \cdot \overrightarrow {AM} \).

b) Tính góc \(\left( {\overrightarrow {AB} ,\overrightarrow {CD} } \right)\).

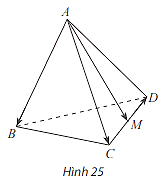
Cho hình lập phương \(ABCD \cdot A'B'C'D'\). Tính góc giữa hai vectơ \(\overrightarrow {BD} ,\overrightarrow {B'C} \).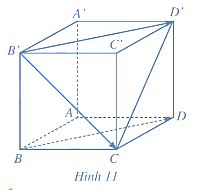

Cho tứ diện \(OABC\) có các cạnh \(OA,OB,OC\) đôi một vuông góc và \(OA = OB = OC = 1\). Gọi \(M\) là trung điểm của cạnh \(AB\). Tính góc giữa hai vectơ \(\overrightarrow {OM} \) và \(\overrightarrow {AC} \).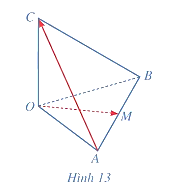

Cho hình chóp \(S \cdot ABCD\) có đáy \(ABCD\) là hình bình hành và mặt bên \(SAB\) là tam giác đều. Tính góc giữa hai vectơ \(\overrightarrow {DC} \) và \(\overrightarrow {BS} \).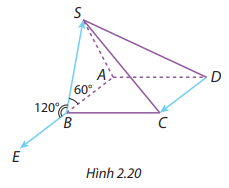

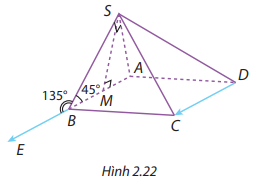
Cho hình chóp \(S \cdot ABCD\) có đáy \(ABCD\) là hình bình hành. Mặt bên \(ASB\) là tam giác vuông cân tại \(S\) và có cạnh \(AB = a\). Gọi \(M\) là trung điểm của \(AB\). Hãy tính:

a) \(\overrightarrow {DC}  \cdot \overrightarrow {BS} \);

b) \(\overrightarrow {DC}  \cdot \overrightarrow {AS} \);

c) \(\overrightarrow {DC}  \cdot \overrightarrow {MS} \).

Cho hình chóp \(S \cdot ABC\) có \(SA = SB = SC = AB = AC = a\) và \(BC = a\sqrt 2 \). Tính góc giữa các vectơ \(\overrightarrow {SC} \) và \(\overrightarrow {AB} \)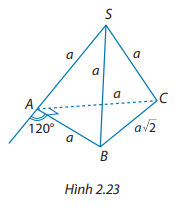

Một chiếc đèn tròn được treo song song vối mặt phẳng nằm ngang bởi ba sợi dây không dãn xuất phát từ điểm \(O\) trên trẩn nhà và lẩn lượt buộc vào ba điểm \(A,B,C\) trên đèn tròn sao cho các lực căng \({\vec F_1},{\vec F_2},{\vec F_3}\) lần lượt trên mỗi dây \(OA,OB,OC\) đôi một vuông góc vởi nhau và \(\left| {{{\vec F}_1}} \right| = \left| {{{\vec F}_2}} \right| = \left| {\overrightarrow {{F_3}} } \right| = 15\left( {{\rm{\;N}}} \right)\) (Hìn 14).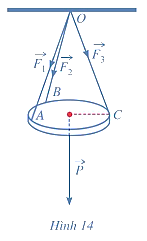

Tính trọng lượng của chiếc đèn tròn đó.

Theo định luật II Newton (Vật lí 10 - Chân trời sáng tạo, Nhà xuất bản Giáo dục Việt Nam, 2023, trang 60): Gia tốc của một vật có cùng hướng với lực tác dụng lên vật. Độ lớn của gia tốc tỉ lệ thuận với độ lớn của lực và tỉ lệ nghịch với khối lượng của vật:

   \(\vec F = m\vec a\)

trong đó \(\vec a\) là vectơ gia tốc \(\left( {{\rm{m}}/{{\rm{s}}^2}} \right),\vec F\) là vectơ lực (N)

Hình 20 tác dụng lên vật, \(m\left( {{\rm{\;kg}}} \right)\) là khối lượng của vật.

Muốn truyền cho quả bóng có khối lượng \(0,5{\rm{\;kg}}\) một gia tốc \(50{\rm{\;m}}/{{\rm{s}}^2}\) thì cần một lực đá có độ lớn là bao nhiêu?

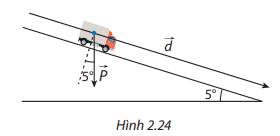
Cho biết công \(A\) (đơn vị: J) sinh bởi lực \(\vec F\) tác dụng lên một vật được tính bằng công thức \(A = \vec F.\vec d\), trong đó \(\vec d\) là vectơ biểu thị độ dịch chuyển của vật (đơn vị của \(\left| {\vec d} \right|\) là \(m\) ) khi chịu tác dụng của lực \(\vec F\). Một chiếc xe có khối lượng 1,5 tấn đang đi xuống trên một đoạn đường dốc có góc nghiêng \({5^ \circ }\) so với phương ngang. Tính công sinh bởi trọng lực \(\vec P\) khi xe đi hết đoạn đường dốc dài \(30{\rm{\;m}}\) (làm tròn kết quả đến hàng đơn vị), biết rằng trọng lực \(\vec P\) được xác định bởi công thức \(\vec P = m\vec g\), với \(m\) (đơn vị: \({\rm{kg}}\) ) là khối lượng của vật và \(\vec g\) là gia tốc rơi tự do có độ lớn \(g = 9,8{\rm{\;m}}/{{\rm{s}}^2}\).