6 bài tập Tích của một số với một vectơ (có lời giải)
6 câu hỏi
Cho hình hộp ABCD. A′B′C′D′ có AC′ và A′C cắt nhau tại O (Hình vẽ)
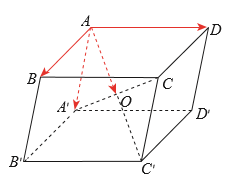
a) Tìm vec tơ \[\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \].
b) Cho biết mối quan hệ giữa vec tơ tìm được ở câu a) và vec tơ \[\overrightarrow {AO} \].
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AD, BC; G là trọng tâm của tam giác BCD. Chứng minh rằng: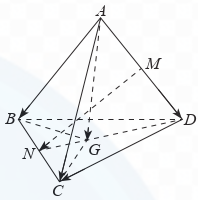
a) \[\overrightarrow {MN} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {DC} } \right)\]
b) \[\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 3\overrightarrow {AG} \]
Cho hình lăng trụ ABC.A′B′C′ có M là trung điểm của BB′ . Đặt \[\overrightarrow {CA} = \overrightarrow a ,\overrightarrow {CB} = {\overrightarrow b _,}\overrightarrow {CC'} \; = {\overrightarrow c _.}\]. Chứng minh rằng: \[\overrightarrow {AM} = \overrightarrow b - \overrightarrow a + \frac{1}{2}{\overrightarrow c _.}\]
Cho tứ diện ABCD có G là trọng tâm của tam giác BCD. Gọi H, K lần lượt là trung điểm của các cạnh AB, AC. Chứng minh rằng:
a) \[\overrightarrow {BC} = 2\overrightarrow {HK} \];
b) \[\overrightarrow {AB} + {\rm{ }}\overrightarrow {AC} + \overrightarrow {AD} = 3\overrightarrow {AG} \].
Cho hình chóp S.ABCD. Gọi I là trọng tâm của tam giác ABC và J là trọng tâm tam giác ADC. Chứng minh rằng: \[2\overrightarrow {SA} + \overrightarrow {SB} + 2\overrightarrow {SC} + \overrightarrow {SD} \; = 3(\overrightarrow {SI} \; + \overrightarrow {SJ} )\].
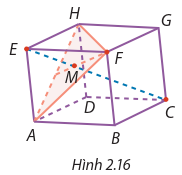
Cho hình hộp ABCD.EFGH. Điểm M là trọng tâm của tam giác AFH (Hình 2.16).
a) Tìm \[\overrightarrow u = \overrightarrow {AB} + \overrightarrow {CB} + \overrightarrow {GH} + \overrightarrow {EH} \]
b) Tìm \[\overrightarrow v = \overrightarrow {FA} - \overrightarrow {BD} \]
c) Chứng minh rằng ba điểm E, M, C thẳng hàng.
d) Tính độ dài của \[\overrightarrow {EM} \] trong trường hợp ABCD.EFGH là hình hộp đứng có các cạnh AB = 5, AD = 6, AE = 10 và \[\widehat {ABC}\] = 120°.