12 bài tập Góc giữa hai vectơ trong không gian – Tích vô hướng (có lời giải)

Cho hình lập phương ABCD.A′B′C′D′. Xác định góc\[(\overrightarrow {AC} ,\overrightarrow {B'D'} ),{\rm{ }}(\overrightarrow {A\prime A} ,\overrightarrow {CB\prime } )\].

Trong không gian, cho \[\overrightarrow u \] và \[\overrightarrow v \] thoả mãn \[\left| {\overrightarrow u } \right| = 2\] và \[\left| {\overrightarrow v } \right| = 3\]. Lấy một điểm A bất kì, gọi B và C là hai điểm sao cho \[\overrightarrow {AB}  = \overrightarrow u ,\overrightarrow {AC}  = \overrightarrow v \] (Hình 24). Giả sử \[\widehat {BAC} = {60^ \circ }\].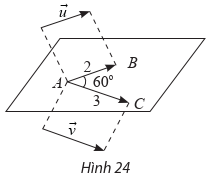

a) Tính góc \[\left( {\overrightarrow u ,\overrightarrow v } \right)\].

b) Trong mặt phẳng (ABC), tính tích vô hướng \[\overrightarrow {AB} .\overrightarrow {AC} \].

Cho tứ diện đều ABCD có cạnh bằng a và M là trung điểm của CD.

a) Tính các tích vô hướng \[\overrightarrow {AB} .\overrightarrow {AC} ,\overrightarrow {AB} {\rm{.}}\overrightarrow {AM} \].

b) Tính góc \[\left( {\overrightarrow {AB} .\overrightarrow {CD} } \right)\].

Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng 1.

a) Tính các tích vô hướng: \[\overrightarrow {AB} .\overrightarrow {A'C'} ,\overrightarrow {AB} {\rm{.}}\overrightarrow {CC'} \].

b) Tính góc \[\left( {\overrightarrow {AC} .\overrightarrow {AC'} } \right)\] (kết quả làm tròn đến phút).

Trong không gian, cho hai vectơ \[\overrightarrow a \] và \[\overrightarrow b \] khác \[\overrightarrow 0 \]. Lấy điểm O và vẽ các vec tơ \[\overrightarrow {OA}  = \overrightarrow a ,\overrightarrow {OB}  = \overrightarrow b \]. Lấy điểm O’ khác O và vẽ các vec tơ \[\overrightarrow {O'A'}  = \overrightarrow a ,\overrightarrow {O'B'}  = \overrightarrow b \]

a) Giải thích vì sao \[\overrightarrow {AB}  = \overrightarrow {A'B'} \]

b) Áp dụng định lí cosin cho hai tam giác OAB và O’A’B’ để giải thích vì sao \[\widehat {AOB} = \widehat {A'O'B'}\].

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và mặt bên SAB là tam giác đều. Tính góc giữa hai vectơ \[\overrightarrow {DC} \] và \[\overrightarrow {BS} \].

Cho hình chóp S.ABC có \(SA = SB = SC = AB = AC = a\) và \(BC = a\sqrt 2 \). Tính góc giữa các vectơ \(\overrightarrow {SC} \) và \(\overrightarrow {AB} \).

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Mặt bên ASB là tam giác vuông cân tại S và có cạnh AB = a. Gọi M là trung điểm của AB. Hăy tính: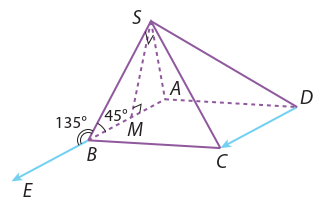

a) \(\overrightarrow {DC}  \cdot \overrightarrow {BS} \);  

b) \(\overrightarrow {DC}  \cdot \overrightarrow {AS} \);

c) \(\overrightarrow {DC}  \cdot \overrightarrow {MS} \).

Cho hình chóp tứ giác đều S.ABCD có độ dài tất cả các cạnh bằng a. Tính các tích vô hướng sau:

a) \[\overrightarrow {AS} \].\[\overrightarrow {BC} \]

b) \[\overrightarrow {AS} \].\[\overrightarrow {AC} \]

c) \[\overrightarrow {AS} \].\[\overrightarrow {BD} \]

d) \[\overrightarrow {AS} \].\[\overrightarrow {CD} \]

Cho hình chóp S.ABC có SA = SB = SC = AB = AC = a và \[BC = a\sqrt 2 \]. Tính góc giữa các vectơ \[\overrightarrow {SC} \] và \[\overrightarrow {AB} \].

Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh đều bằng a và \[\widehat {BAA'} = \widehat {BAD} = \widehat {DAA'} = {60^o}\].

a) Chứng minh rằng: \[\overrightarrow {A'C} .\overrightarrow {B'D'}  = 0\]

b) Tính độ dài đường chéo AC’.