9 bài tập Tổng và hiệu của hai vectơ (có lời giải)
8 câu hỏi
Cho hình hộp ABCD.A′B′C′D′ (Hình vẽ).
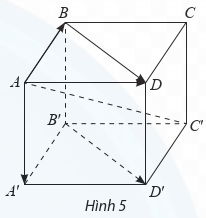
a) Trong mặt phẳng (ABCD), tìm vectơ tổng \[\overrightarrow {AB} + \overrightarrow {AD} \].
b) So sánh hai vectơ \[\overrightarrow {BD} ,\overrightarrow {B'D'} \].
c) Giải thích tại sao \[\overrightarrow {AB} + \overrightarrow {B'D'} = \overrightarrow {AD} \].
Cho hình lăng trụ ABC.A′B′C′. Tìm các vectơ tổng \[\overrightarrow {BA} + \overrightarrow {A'C'} ;\overrightarrow {BC} + \overrightarrow {AA'} \].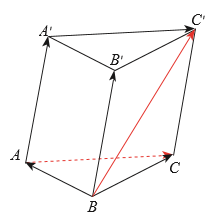
Cho hình hộp ABCD.A′B′C′D′.
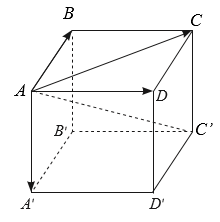
a) Tìm các vectơ tổng\[\overrightarrow {AB} + \overrightarrow {AD} ;\overrightarrow {AC} + \overrightarrow {AA'} \].
b) Dùng kết quả của câu a và tính chất kết hợp của phép cộng vectơ để chứng minh \[\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \].
Cho hình hộp ABCD.EFGH. Thực hiện các phép toán sau đây:
a) \[\overrightarrow {CB} + \overrightarrow {CD} + \overrightarrow {CG} \]
b) \[\overrightarrow {DA} + \overrightarrow {DC} + \overrightarrow {DH} \]
c) \[\overrightarrow {AB} + \overrightarrow {CG} + \overrightarrow {EH} \]
d) \[\overrightarrow {HE} + \overrightarrow {GC} + \overrightarrow {AB} \]
Cho tứ diện ABCD có M và N lần lượt là trung điểm của AB và CD. Hãy thực hiện các phép toán sau đây:
a) \[\overrightarrow {BM} + \overrightarrow {AC} + \overrightarrow {ND} \]
b) \[\overrightarrow {AD} - \overrightarrow {AM} + \overrightarrow {NC} \]
Cho hình lập phương ABCD. A′B′C′D′ có cạnh bằng đơn vị. Tìm độ dài các vectơ sau đây:
a) \[\overrightarrow a = \overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {BB'} \]
b) \[\overrightarrow b = \overrightarrow {BC} - \overrightarrow {BA} + \overrightarrow {C'A} \]
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi E, F lần lượt là các điểm thuộc các cạnh SA, SB sao cho \[SE = \frac{1}{3}SA,SF = \frac{1}{3}SB.\] Chứng minh rằng \[\overrightarrow {EF} = \frac{1}{3}\overrightarrow {DC} \].
Cho hình lăng trụ tam giác ABC.A′B′C′ có \[\overrightarrow {AA'} = \;\overrightarrow {a,} {\rm{ }}\overrightarrow {AB} = \;\overrightarrow b ,\overrightarrow {AC} = \overrightarrow c \]. Chứng minh rằng \[\overrightarrow {B'C} = \;\overrightarrow c - \overrightarrow a - \;\overrightarrow b \] và \[\overrightarrow {BC'} = \;\overrightarrow a - \;\overrightarrow b + \overrightarrow c \].








