(Đúng sai) 26 bài tập Vectơ và các phép toán trong không gian (có lời giải)

b) Tam giác \(SBD\) cân tại \(S\).

c)  \(\left( {\overrightarrow {SB} ,\overrightarrow {BD} } \right) = {45^0}\).

d) \(\overrightarrow {SB} \,.\,\overrightarrow {BD}  =  - {a^2}\).

a)  Cho tứ diện \(ABCD\). Hỏi có bao nhiêu véctơ khác véctơ \(\overrightarrow 0 \) mà mỗi véctơ có điểm đầu, điểm cuối là hai đỉnh của tứ diện\(ABCD\) là 12.

b) Cho hình hộp \[ABCD.A'B'C'D'\] (xem hình dưới), tổng của \[\overrightarrow {DA}  + \overrightarrow {DC}  + \overrightarrow {DD'} \] là vectơ \(\overrightarrow {DB'} \)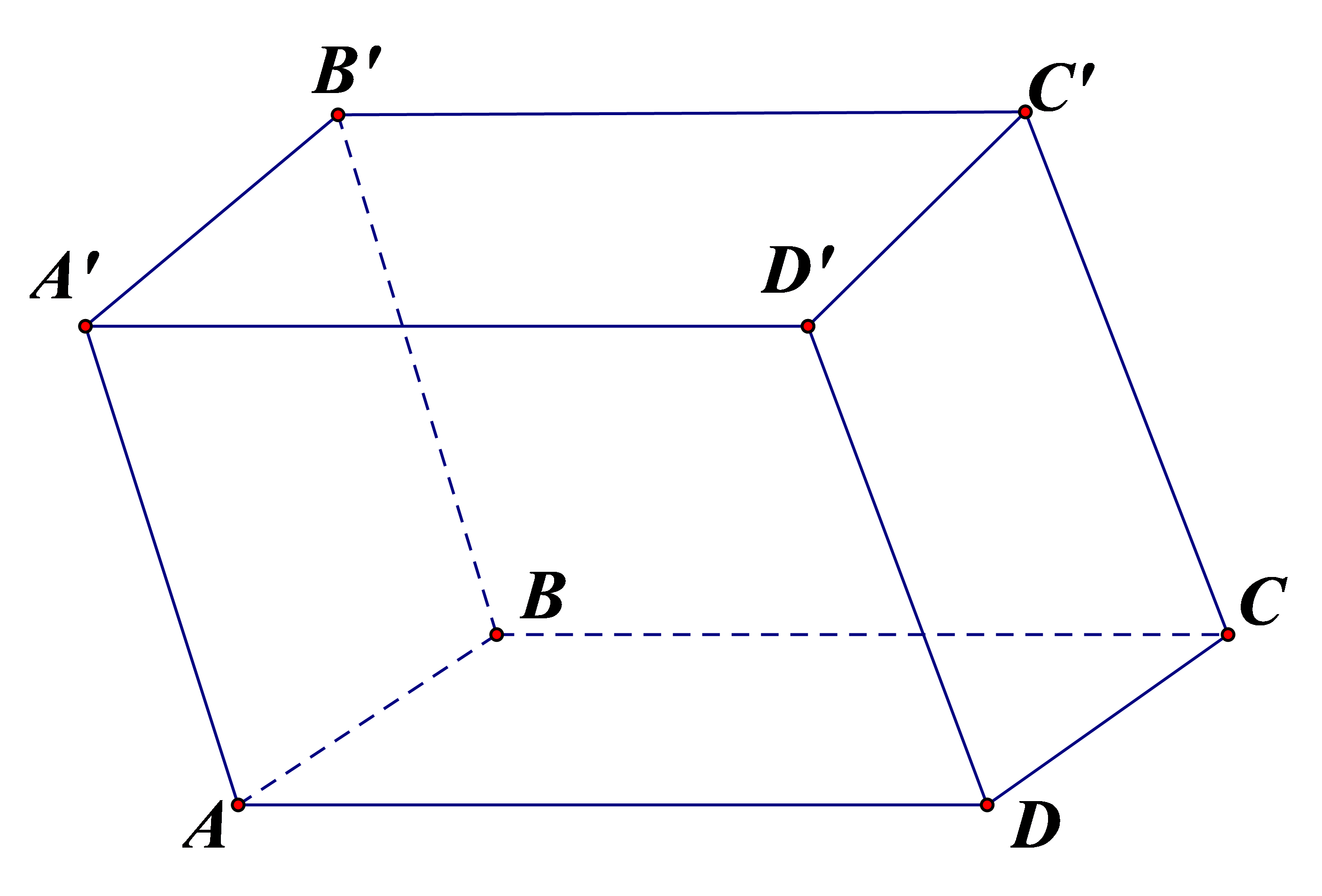

c)  Nếu giá của ba vec tơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) cắt nhau từng đôi một thì ba vec tơ đó đồng phẳng.

d) Cho hình lập phương (tham khảo hình vẽ) có cạnh bằng . Tính \[\overrightarrow {AB} .\overrightarrow {DC'}  = {a^2}\]

a)  \(\overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AA'}  = \overrightarrow {AC'} \)

b) \(\overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {AA'}  = \overrightarrow {AC'} \)

c)  \(\overrightarrow {AC}  + \overrightarrow {AD}  + \overrightarrow {AA'}  = \overrightarrow {AC'} \)

d)  \(\overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {AA'}  = \overrightarrow {AC} \)

a)  \(\overrightarrow {BA}  + \overrightarrow {BC}  + \overrightarrow {BB'}  = \overrightarrow {BD'} \)

b) \(\overrightarrow {BA}  + \overrightarrow {BC}  + \overrightarrow {BB'}  = \overrightarrow {BD} \)

c)  \(\overrightarrow {BA}  + \overrightarrow {BC}  + \overrightarrow {BB'}  = \overrightarrow {BC'} \)

d)  \(\overrightarrow {BA}  + \overrightarrow {BC}  + \overrightarrow {BB'}  = \overrightarrow {BA'} \)

a)  Cho hình hộp \(ABCDEFGH\)(tham khảo hình vẽ). Tính tổng ba véctơ \(\overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {AE} \) = \(\overrightarrow {AG} \).

b) Cho hình hộp \(ABC{\rm{D}}.A'B'C'D'\). Các véc tơ có điểm đầu và điểm cuối là các đỉnh của hình hộp và bằng véc tơ \(\overrightarrow {AB} \) là \(\overrightarrow {DC} ;{\rm{ }}\overrightarrow {A'B'} ;{\rm{ }}\overrightarrow {D'C'} \)

c)  Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\). Khi đó, vectơ bằng vectơ \(\overrightarrow {AB} \) là vectơ  \(\overrightarrow {D'C'} \)

d)  Cho tứ diện ABCD. Hỏi có bao nhiêu vectơ khác vectơ \(\overrightarrow 0 \) mà mỗi vectơ có điểm đầu, điểm cuối là hai đỉnh của tứ diện ABCD là 12.

a) Nếu trong ba vectơ \(\overrightarrow a ,\,\,\overrightarrow b ,\,\,\overrightarrow c \) có một vectơ bằng \(\overrightarrow 0 \) thì ba vectơ \(\overrightarrow a ,\,\,\overrightarrow b ,\,\,\overrightarrow c \) đồng phẳng.

b) Nếu giá của ba vectơ \(\overrightarrow a ,\,\,\overrightarrow b ,\,\,\overrightarrow c \) cùng song song với một mặt phẳng thì ba vectơ \(\overrightarrow a ,\,\,\overrightarrow b ,\,\,\overrightarrow c \) đồng phẳng.

c)  Nếu trong ba vectơ \(\overrightarrow a ,\,\,\overrightarrow b ,\,\,\overrightarrow c \) có hai vectơ cùng phương thì ba vectơ \(\overrightarrow a ,\,\,\overrightarrow b ,\,\,\overrightarrow c \) đồng phẳng.

d) Nếu giá của ba vectơ \(\overrightarrow a ,\,\,\overrightarrow b ,\,\,\overrightarrow c \) đồng quy thì ba vectơ \(\overrightarrow a ,\,\,\overrightarrow b ,\,\,\overrightarrow c \) đồng phẳng.

a)  Cho \[\overrightarrow a ,\,\overrightarrow {\;b} ,\,\;\overrightarrow c \] đều khác \[\overrightarrow 0 \]. Ba véctơ \[\overrightarrow a ,\,\overrightarrow {\;b} ,\,\;\overrightarrow c \] đồng phẳng khi và chỉ khi giá của chúng cùng nằm trên một mặt phẳng.

b) Với tứ diện ABCD bất kì ta luôn có \[\overrightarrow {AC}  + \overrightarrow {BD}  = \overrightarrow {AD}  + \overrightarrow {BC} .\]

c) Một đường thẳng cắt hai đường thẳng cho trước thì tồn tại một mặt phẳng chứa cả ba đường thẳng đó.    

d) Với hình hộp \[ABCD.A'B'C'D'\] bất kì ta luôn có \[\overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {AA'}  = \overrightarrow {C'A} .\]

Các mệnh đề sau đúng hay sai?

a)  Tứ giác\(ABCD\)là hình bình hành nếu \(\overrightarrow {AB}  + \overrightarrow {BC}  + \overrightarrow {CD}  + \overrightarrow {DA}  = \overrightarrow 0 \).

Các mệnh đề sau đúng hay sai?

b)Tứ giác\(ABCD\)là hình bình hành nếu $\overrightarrow{AB}=\overrightarrow{CD}$

Các mệnh đề sau đúng hay sai?

c)   Cho hình chóp \(S.ABCD\). Nếu có \(\overrightarrow {SB}  + \overrightarrow {SD}  = \overrightarrow {SA}  + \overrightarrow {SC} \)thì tứ giác \(ABCD\)là hình bình hành.

Các mệnh đề sau đúng hay sai?

d)  Tứ giác \(ABCD\)là hình bình hành nếu \(\overrightarrow {AB}  + \overrightarrow {AC}  = \overrightarrow {AD} \).

Các mệnh đề sau đúng hay sai?a)  Ba véc tơ \[\overrightarrow a \,,\,\overrightarrow b \,,\,\overrightarrow c \]đồng phẳng nếu có hai trong ba véc tơ đó cùng phương.

Các mệnh đề sau đúng hay sai?b) Ba véc tơ \[\overrightarrow a \,,\,\overrightarrow b \,,\,\overrightarrow c \]đồng phẳng nếu có một trong ba véc tơ bằng véc tơ \[\overrightarrow 0 \].

Các mệnh đề sau đúng hay sai?c) Véc tơ \[\overrightarrow x  = \overrightarrow a  + \overrightarrow b  + \overrightarrow c \]luôn đồng phẳng với hai véc tơ \[\overrightarrow a \,\]và \[\,\overrightarrow b \,\].

Các mệnh đề sau đúng hay sai?d) Trong hình hộp \[ABCD.A'B'C'D'\]ba véc tơ \[\overrightarrow {AB'} \,,\,\overrightarrow {C'A'} \,,\,\overrightarrow {DA'} \]đồng phẳng.

Các mệnh đề sau đúng hay sai?

a) Cho hình hộp \(ABCD.A'B'C'D'\). Thực hiện phép toán \(\overrightarrow u  = \overrightarrow {A'D'}  + \overrightarrow {A'B'}  + \overrightarrow {A'A} \)bằng \(\overrightarrow u  = \overrightarrow {A'C} \)

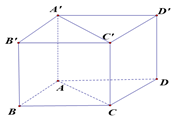
Các mệnh đề sau đúng hay sai?b) Cho tứ diện \(ABCD\). Gọi \(G\) là trọng tâm tam giác \(ABD\). Khi đó\(\overrightarrow {CA}  + \overrightarrow {CB}  + \overrightarrow {CD}  = 3\overrightarrow {CG} \)

Các mệnh đề sau đúng hay sai?c) Cho hình lăng trụ \(ABC.A'B'C'\). Đặt \(\overrightarrow a  = \overrightarrow {AA'} \), \(\overrightarrow b  = \overrightarrow {AB} \), \(\overrightarrow c  = \overrightarrow {AC} \). Gọi \(G'\) là trọng tâm của tam giác \(A'B'C'\). Vectơ \(\overrightarrow {AG'} \) bằng\(\overrightarrow {AG'}  = \frac{1}{3}\left( {\overrightarrow a  + \overrightarrow b  + \overrightarrow c } \right)\)

 Các mệnh đề sau đúng hay sai?

d) Cho hình lập phươn g \[ABCD.A'B'C'D'\] cạnh \[a\]. Đặt \[\overrightarrow x  = \overrightarrow {AA'}  + \overrightarrow {AC'} \]. Độ dài của \[\overrightarrow x \] bằng\[a\sqrt 2 \]

a)  \(\overrightarrow {AC'}  = \overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {AA'} \)

b) \(\overrightarrow {AB}  + \overrightarrow {B'C'}  = \overrightarrow {A'C'} \)

c) \(\overrightarrow {BD'}  = \overrightarrow {C'D'}  + \overrightarrow {B'C'}  + \overrightarrow {AA'} \)

d) \(\overrightarrow {AB}  + \overrightarrow {B'C'}  + \overrightarrow {CD}  = \vec 0\)

a)  \(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD}  = \overrightarrow 0 \)

b) \(\overrightarrow {AG}  + \overrightarrow {BG}  + \overrightarrow {CG}  + \overrightarrow {DG}  = 0\)

c) $GA=GB=GC=GD$

d) $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$

Cho hình hộp \(ABCD.A'B'C'D'\). Gọi \(I,\,\,J\) lần lượt là trung điểm của \(AB'\) và \(CD'\). Các mệnh đề sau đúng hay sai?a) $\overrightarrow{AI}=\overrightarrow{CJ}$

Cho hình hộp \(ABCD.A'B'C'D'\). Gọi \(I,\,\,J\) lần lượt là trung điểm của \(AB'\) và \(CD'\). Các mệnh đề sau đúng hay sai?b) $\overrightarrow{D^{\text{'}}{A}^{\text{'}}}=\overrightarrow{IJ}$

Cho hình hộp \(ABCD.A'B'C'D'\). Gọi \(I,\,\,J\) lần lượt là trung điểm của \(AB'\) và \(CD'\). Các mệnh đề sau đúng hay sai?c) $\overrightarrow{BI}=\overrightarrow{D^{\text{'}}J}$

Cho hình hộp \(ABCD.A'B'C'D'\). Gọi \(I,\,\,J\) lần lượt là trung điểm của \(AB'\) và \(CD'\). Các mệnh đề sau đúng hay sai?d) $\overrightarrow{A^{\text{'}}I}=\overrightarrow{JC}$

Các mệnh đề sau đúng hay sai?a)  Cho tứ diện \(ABCD\). Gọi \(G\) là trọng tâm tam giác \(ABD\). Khi đó\(\overrightarrow {CA}  + \overrightarrow {CB}  + \overrightarrow {CD}  = 3\overrightarrow {CG} \)

Các mệnh đề sau đúng hay sai?b) Cho hình lăng trụ \(ABC.A'B'C'\). Đặt \(\overrightarrow a  = \overrightarrow {AA'} \), \(\overrightarrow b  = \overrightarrow {AB} \), \(\overrightarrow c  = \overrightarrow {AC} \). Gọi \(G'\) là trọng tâm của tam giác \(A'B'C'\). Vectơ \(\overrightarrow {AG'} \) bằng\(\overrightarrow {AG'}  = \frac{1}{3}\left( {3\overrightarrow a  + \overrightarrow b  + \overrightarrow c } \right)\)

Các mệnh đề sau đúng hay sai?c) Cho tứ diện \(ABCD\). Gọi \(G\) là trọng tâm tam giác \(ABD\). Khi đó: \(\overrightarrow {CA}  + \overrightarrow {CB}  + \overrightarrow {CD}  = 3\overrightarrow {CG} \)

Các mệnh đề sau đúng hay sai?d)  Cho hình lập phương \[ABCD.A'B'C'D'\] cạnh \[a\]. Đặt \[\overrightarrow x  = \overrightarrow {AA'}  + \overrightarrow {AC'} \]. Độ dài của \[\overrightarrow x \] bằng\[\frac{{a\sqrt 6 }}{2}\]

Cho tứ diện ABCD. Các mệnh đề sau đúng hay sai?a)  \(\overrightarrow {BC}  + \overrightarrow {AB}  = \overrightarrow {DA}  - \overrightarrow {DC} \).

Cho tứ diện ABCD. Các mệnh đề sau đúng hay sai?

b) $\overrightarrow{AC}-\overrightarrow{AD}=\overrightarrow{BD}-\overrightarrow{BC}$

Cho tứ diện ABCD. Các mệnh đề sau đúng hay sai?

c) $\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{DB}-\overrightarrow{DC}$

Cho tứ diện ABCD. Các mệnh đề sau đúng hay sai?

d) $\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{CD}+\overrightarrow{BC}$

Cho hình hộp \[ABCD.A'B'C'D'.\] Các mệnh đề sau đúng hay sai?

a)  \[\overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {AA'}  = \overrightarrow {AD'} \]

Cho hình hộp \[ABCD.A'B'C'D'.\] Các mệnh đề sau đúng hay sai?

b) $\overrightarrow{CD}+\overrightarrow{CB}+\overrightarrow{C{C}^{\text{'}}}=\overrightarrow{C{A}^{\text{'}}}$

Cho hình hộp \[ABCD.A'B'C'D'.\] Các mệnh đề sau đúng hay sai?

c) $\overrightarrow{DA}+\overrightarrow{DC}+\overrightarrow{DB}=\overrightarrow{D{B}^{\text{'}}}$

Cho hình hộp \[ABCD.A'B'C'D'.\] Các mệnh đề sau đúng hay sai?

d) $\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{BD}=\overrightarrow{B{D}^{\text{'}}}$

Các mệnh đề sau đúng hay sai?

a) Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi O là tâm hình vuông ABCD và điểm S thỏa mãn $\overrightarrow{OS}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}+\overrightarrow{O{A}^{\text{'}}}+\overrightarrow{O{B}^{\text{'}}}+\overrightarrow{O{C}^{\text{'}}}+\overrightarrow{O{D}^{\text{'}}}$. Vậy độ dài đoạn $OS=4a$

Các mệnh đề sau đúng hay sai?

b)Hình lập phương \(ABCD.A'B'C'D'\)cạnh \(a\). Vậy độ dài véctơ $\overrightarrow{x}=\overrightarrow{A{A}^{\text{'}}}+\overrightarrow{A{C}^{\text{'}}}=\frac{a\sqrt{6}}{2}$

Các mệnh đề sau đúng hay sai?

c)  Cho tứ diện \(ABCD\), gọi \(G\) là trọng tâm của tam giác \(BCD\). Biết luôn tồn tại số thực \(k\) thỏa mãn đẳng thức vecto $\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}=k.\overrightarrow{AG}$. Hỏi số thực đó bằng 4

Các mệnh đề sau đúng hay sai?

d)  Cho hình chóp \[S.ABCD\] có tất cả các cạnh bên và cạnh đáy đều bằng \[a\] và \[ABCD\] là hình vuông. Gọi \[M\] là trung điểm của \[CD.\] Giá trị \(\overrightarrow {MS} .\overrightarrow {CB} \) bằng\[\frac{{{a^2}}}{3}\]

a)  \(\overrightarrow {GA}  + \overrightarrow {GC}  = 2\overrightarrow {GM} \)

b) \(G\) là trọng tâm của tứ diện \(ABCD\).

c) \(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD}  = \vec 0\)

d) \(\overrightarrow {GB}  + \overrightarrow {GD}  = 2\overrightarrow {MN} \)

Cho tứ diện \(ABCD\). Gọi \(I\) là trung điểm \(CD\). Các mệnh đề sau đúng hay sai?

a) $\overrightarrow{AI}=\frac{1}{2}\overrightarrow{AC}+\frac{1}{2}\overrightarrow{AD}$

Cho tứ diện \(ABCD\). Gọi \(I\) là trung điểm \(CD\). Các mệnh đề sau đúng hay sai?

b) \(\overrightarrow {BI}  = \overrightarrow {BC}  + \overrightarrow {BD} \)

Cho tứ diện \(ABCD\). Gọi \(I\) là trung điểm \(CD\). Các mệnh đề sau đúng hay sai?

c) $\overrightarrow{BI}=\frac{1}{2}\overrightarrow{BC}-\frac{1}{2}\overrightarrow{BD}$

Cho tứ diện \(ABCD\). Gọi \(I\) là trung điểm \(CD\). Các mệnh đề sau đúng hay sai?

d) $\overrightarrow{AI}=\overrightarrow{AC}+\overrightarrow{AD}$

Các mệnh đề sau đúng hay sai?

a)  Cho tứ diện \(ABCD\), gọi \(G\) là trọng tâm của tam giác \(BCD\). Biết luôn tồn tại số thực \(k\) thỏa mãn đẳng thức vecto \(\overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD}  = k.\overrightarrow {AG} \).Vậy số thực đó bằng \(3\)

Các mệnh đề sau đúng hay sai?

b) Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng \(a\). Gọi \(O\) là tâm hình vuông \(ABCD\) và điểm \[20\] thỏa mãn $\overrightarrow{OS}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}+\overrightarrow{O{A}^{\text{'}}}+\overrightarrow{O{B}^{\text{'}}}+\overrightarrow{O{C}^{\text{'}}}+\overrightarrow{O{D}^{\text{'}}}$. Vậy độ dài đoạn \[OS\] theo \(a\)là\(OS = 4a\)

Các mệnh đề sau đúng hay sai?

c)  Hình lập phương \(ABCD.A'B'C'D'\)cạnh \(a\).Vậy độ dài véctơ $\overrightarrow{x}=\overrightarrow{A{A}^{\text{'}}}+\overrightarrow{A{C}^{\text{'}}}$ theo \(a\)là \(a\sqrt 6 \)

Các mệnh đề sau đúng hay sai?

d)  Cho hình chóp \[S.ABCD\] có tất cả các cạnh bên và cạnh đáy đều bằng \[a\] và \[ABCD\] là hình vuông. Gọi \[M\] là trung điểm của \[CD.\] Giá trị \(\overrightarrow {MS} .\overrightarrow {CB} \) bằng\( - \frac{{{a^2}}}{2}\)

a)  \(\overrightarrow {GA} + \overrightarrow {GC} = 2\overrightarrow {GM} \)

b) \(\overrightarrow {GB}  + \overrightarrow {GD}  = \overrightarrow {MN} \)

c)  \(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD}  = \vec 0\)

d)  \(2\overrightarrow {NM}  = \overrightarrow {AB}  + \overrightarrow {CD} \)

a)  \(\overrightarrow {AM}  = \overrightarrow a  + \overrightarrow c  - \frac{1}{2}\overrightarrow b \)

b) \(\overrightarrow {AM}  = \overrightarrow a  - \overrightarrow c  + \frac{1}{2}\overrightarrow b \)

c)  \(\overrightarrow {AM}  = \overrightarrow b  + \overrightarrow c  - \frac{1}{2}\overrightarrow a \)

d)  \(\overrightarrow {AM}  = \overrightarrow b  - \overrightarrow a  + \frac{1}{2}\overrightarrow c \)

a)  \[\overrightarrow {BD'}  = \overrightarrow {BA}  + \overrightarrow {BC}  + \overrightarrow {BB'} \]

b) \[\overrightarrow {AC'}  = \overrightarrow {AC}  + \overrightarrow {AB}  + \overrightarrow {AD} \]

c)  \[\overrightarrow {DB}  = \overrightarrow {DA}  + \overrightarrow {DD'}  + \overrightarrow {DC} \]

d)  \[\overrightarrow {AB'}  = \overrightarrow {AB}  + \overrightarrow {AA'}  + \overrightarrow {AD} \]

Các mệnh đề sau đúng hay sai?

a) Cho tứ diện đều \(ABCD\) . Tích vô hướng \(\overrightarrow {AB} .\overrightarrow {CD} \) bằng\(0\)

Các mệnh đề sau đúng hay sai?

b) Cho hình lăng trụ \[ABC.A'B'C'\]. \[M\] là trung điểm của \[BB'\]. Đặt \[\overrightarrow {CA}  = \overrightarrow a ,\overrightarrow {CB}  = \overrightarrow b ,\overrightarrow {AA'}  = \overrightarrow {c.} \] Khi đó\[\overrightarrow {AM}  =  - \frac{{\overrightarrow a }}{2} + \overrightarrow b  + \overrightarrow c \]

Các mệnh đề sau đúng hay sai?

c) Cho lăng trụ tam giác \[ABC.A'B'C'\]có \[\overrightarrow {{\rm{AA}}'}  = \overrightarrow a \], \[\overrightarrow {{\rm{AB}}}  = \overrightarrow b \], \[\overrightarrow {{\rm{AC}}}  = \overrightarrow c \]. Hãy phân tích (biểu thị) vectơ \[\overrightarrow {{\rm{BC'}}} \]qua các vectơ \[\overrightarrow a \], \[\overrightarrow b \],\[\overrightarrow c \].vậy\[\overrightarrow {BC'}  = \overrightarrow a  - \overrightarrow b  + \overrightarrow c \]

Các mệnh đề sau đúng hay sai?

d) Cho hình lăng trụ\(ABC.A'B'C'\) với \(G\) là trọng tâm của tam giác \(A'B'C'.\) Đặt \[\overrightarrow {AA'}  = \overrightarrow a \], \[\overrightarrow {AB}  = \overrightarrow b \], \[\overrightarrow {AC}  = \overrightarrow c \]. Khi đó \(\overrightarrow {AG} \) bằng: \(\overrightarrow a  + \frac{1}{4}\left( {\overrightarrow b  + \overrightarrow c } \right).\;\)

Cho hình hộp \[ABCD.A'B'C'D'\]. Các mệnh đề sau đúng hay sai?

a)  \(\overrightarrow {AC'}  = \overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD} \)

Cho hình hộp \[ABCD.A'B'C'D'\]. Các mệnh đề sau đúng hay sai?

b) $\overrightarrow{A{C}^{\text{'}}}=\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{A{A}^{\text{'}}}$

Cho hình hộp \[ABCD.A'B'C'D'\]. Các mệnh đề sau đúng hay sai?

c) $\overrightarrow{A{C}^{\text{'}}}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{A{A}^{\text{'}}}$

Cho hình hộp \[ABCD.A'B'C'D'\]. Các mệnh đề sau đúng hay sai?

d) $\overrightarrow{A{C}^{\text{'}}}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{A{B}^{\text{'}}}$

a)  \(\overrightarrow {AM}  =  - \overrightarrow b  + \overrightarrow c  + \frac{1}{2}\overrightarrow a \)

b) \(\overrightarrow {AM}  = \overrightarrow b  + \overrightarrow c  - \frac{1}{2}\overrightarrow a \)

c)  \(\overrightarrow {AM}  = \overrightarrow b  - \overrightarrow a  + \frac{1}{2}\overrightarrow c \)

d)  \(\overrightarrow {AM}  = \overrightarrow a  - \overrightarrow c  + \frac{1}{2}\overrightarrow b \)