Đề thi Học kì 1 Toán 10 Cánh diều có đáp án - Đề 1

Trong các câu sau, câu nào không là mệnh đề ?

Cặp số $(x;y)$ nào sau đây không là nghiệm của bất phương trình $4x-9y-3\ge 0$?

Cách viết nào sau đây là đúng?

Cho hình vẽ sau:

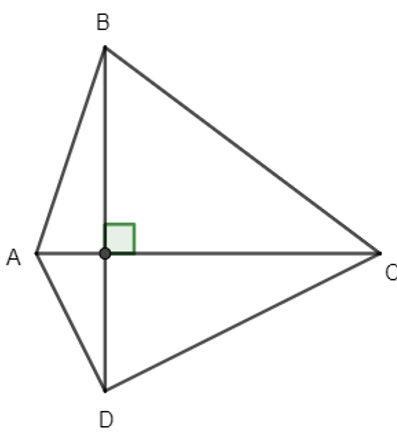
Tích vô hướng của hai vectơ nào bằng 0?

Cho hình thoi ABCD  cạnh a và $\widehat{ABD}=60°$. Độ dài vectơ $\overrightarrow{BD}$ là

Tính $\overrightarrow{AD}-\overrightarrow{AC}+\overrightarrow{DC}$                          

Với α∈ (120°; 270°) thì giá trị lượng giác nào dưới đây nhận giá trị âm?

A. sinα;

B. cosα;

C. tanα;                                                          

D. cotα.

Trong các bất phương trình sau, bất phương trình bậc nhất hai ẩn là

Cho đồ thị hàm số sau:

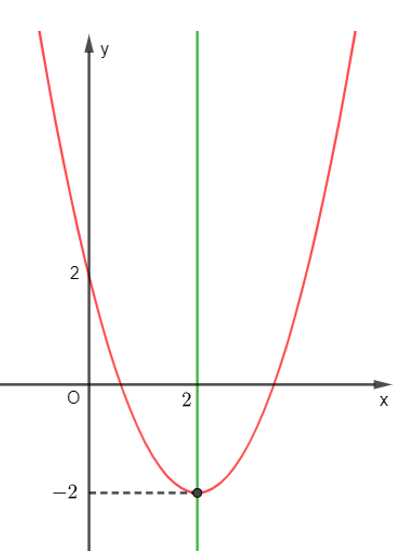
Đồ thị hàm số trên là của hàm số nào dưới đây?

Cho tam giác ABC, có G là trọng tâm tam giác, M là điểm bất kì. Biểu thức nào sau đây là đúng?

Cho đồ thị hàm số:

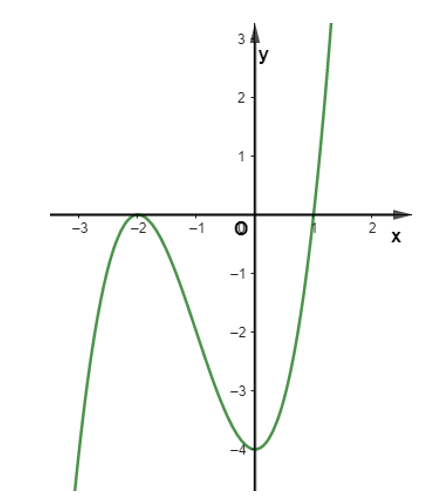
Hàm số đồng biến trên khoảng

Hàm số f(x) = x² – 2x + 1 nhận giá trị dương khi

Cặp số (0; 1) là nghiệm của hệ bất phương trình nào sau đây?

Cho hàm số y = f(x) có bảng biến thiên sau:

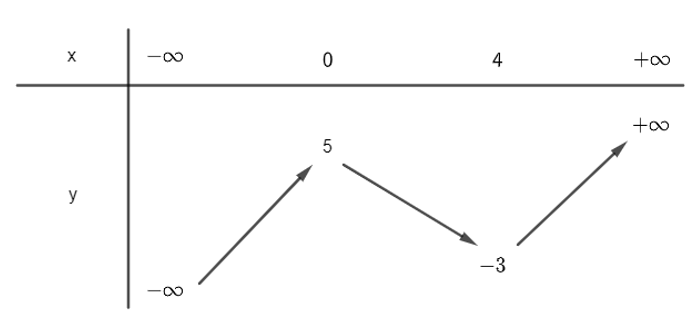
Tập giá trị của hàm số f(x) là:

Cho các bất phương trình sau:

– 2x + 1 < 0; $\frac{1}{2}{y}^2-\sqrt{2}\left(y-1\right)\le 0$; $x^2-\sqrt{x}>0$; y² + x² – 2x < 0.

Có bao nhiêu bất phương trình không là bất phương trình bậc hai một ẩn?

Hàm số bậc hai y = 2x² – $\frac{1}{3}$x có trục đối xứng là

Tập nghiệm của bất phương trình x² – 5x + 6 < 0 là

A. S = (2; 3);

B. S = (– ∞; 2);    

C. S = (3; +∞);            

D. S = (– ∞; 2) ∪ (3; +∞).

Để giải phương trình: $\sqrt{3x-1}=x^2-1$ cần điều kiện:

Lớp 10B có 45 học sinh, trong đó có 25 em thích môn Văn, 20 em thích môn Toán, 18 em thích môn Sử, 6 em không thích môn nào, 6 em thích cả Sử và Toán, 8 em thích cả Văn và Toán, 5 em thích cả ba môn. Số học sinh thích cả Văn và Sử là

Tam giác ABC có $AB=3,AC=6$ và $\widehat{A}=60°$. Bán kính R của đường tròn ngoại tiếp tam giác ABC là

Trong các công thức dưới đây, công thức nào tính diện tích tam giác ABC là đúng?

A. S_ABC = $\frac{1}{2}b.c.\cos A$;  

B. S_ABC = $\frac{abc}{4R}$;             

C. S_ABC = pR;               

D. S_ABC = a.h_a.

Tính giá trị biểu thức: cos20° + cos40° + cos60° + ... + cos160° + cos180°.

Cho hàm số $f\left(x\right)=\frac{\sqrt{2x+4}}{x-\sqrt{x}-2}$. Tập xác định D của hàm số là

Cho tam giác ABC có AB=5, BC=7, CA=8 . Tam giác ABC là

Cho tam giác ABC có M là trung điểm của AC, N là trung điểm của BC và AB = a. Độ dài vectơ $\overrightarrow{CM}-\overrightarrow{NB}$ bằng

Cho 90° <α< 180°. Xác định dấu của biểu thức M = sin(90° – α).cot(180° + α).

A. M ≥ 0;   

B. M ≤ 0;                     

C. M > 0;                     

D. M < 0.

Cho tam giác ABC đều cạnh bằng a, AH là đường cao. Tính $\overrightarrow{AB}.\overrightarrow{AH}$

Cho tứ giác ABCD, có I, J lần lượt là trung điểm của AB và CD. Ta có $\overrightarrow{\text{IJ}}=a\overrightarrow{AC}+b\overrightarrow{BD}$. Khi đó a – b bằng

Cho phương trình: $\sqrt{x^2-5x+1}=\sqrt{x-7}$. Số nghiệm của phương trình là

Một rạp chiếu phim có sức chứa 1 000 người. Với giá vé là 40 000 đồng, trung bình sẽ có khoảng 300 người đến rạp xem phim mỗi ngày. Để tăng số lượng vé bán ra, rạp chiếu phim đã khảo sát thị trường và thấy rằng giá vé cứ giảm 10 000 đồng thì sẽ có thêm 100 người đến rạp mỗi ngày.

a) Tìm công thức của hàm số R(x) mô tả doanh thu từ tiền bán vé mỗi ngày của rạp chiếu phim khi giá vé là x nghìn đồng.

b) Tìm mức giá vé để doanh thu từ tiền bán vé mỗi ngày của rạp là lớn nhất.

a) Giải phương trình: $x-2+3\sqrt{x^2-2x-3}=7$.

b) Tìm m để hàm số f(x) = x² – 2(m + 3)x – 4m + 1 > 0 với mọi số thực x.

Cho tam giác ABC, gọi I và J là hai điểm được xác định bởi $\overrightarrow{IA}=2\overrightarrow{IB}$, $3\overrightarrow{JA}+2\overrightarrow{JC}=\overrightarrow{0}$.

a) Tính $\overrightarrow{\text{IJ}}$ theo $\overrightarrow{AB}$ và $\overrightarrow{AC}$.

b) Chứng minh đường thẳng IJ đi qua trọng tâm G của tam giác ABC.