Bộ 10 đề thi Giữa kì 1 Toán 10 Cánh Diều có đáp án - Đề 4
28 câu hỏi
I. PHẦN TRẮC NGHIỆM (7 điểm)
Cho mệnh đề chứa biến . Với giá trị nào của a ta được mệnh đề sai?
\(a = - 2\);
\(a = 7\);
\(a = - 1\);
\(a = 1\).
Câu nào dưới đây là một mệnh đề?
“Tháng 8 dương lịch có 31 ngày.”;
“Số 2 022 có chia hết cho 20 không?”;
“Vườn hoa này đẹp quá!”;
“Cảnh báo đường trơn, hãy lái xe cẩn thận!”.
Mệnh đề phủ định của mệnh đề: “số 12 chia hết cho 4 và 3” là
“Số 12 hoặc chia hết cho 4 hoặc chia hết cho 3”;
“Số 12 không chia hết cho 4 và không chia hết cho 3”;
“Số 12 không chia hết cho 4 hoặc không chia hết cho 3”;
“Số 12 không chia hết cho 4 và chia hết cho 3”.
Mệnh đề nào dưới đây là đúng?
\(\forall x \in \mathbb{R},{x^2} > 1 \Rightarrow x > - 1\);
\(\forall x \in \mathbb{R},{x^2} > 1 \Rightarrow x > 1\);
\(\forall x \in \mathbb{R},x > - 1 \Rightarrow {x^2} > 1\);
\(\forall x \in \mathbb{R},x > 1 \Rightarrow {x^2} > 1\).
Cho hai tập hợp \[A = \left\{ {1;\,2;\,3} \right\}\] và \[B = \left\{ {1;\,2;\,3;\,4;\,5} \right\}\]. Có tất cả bao nhiêu tập \[X\] thỏa mãn \[A \subset X \subset B\]?
\[4\];
\[5\];
\[6\];
\[8\].
Cho hai tập hợp \(A = \left[ { - 2;\,3} \right]\) và \(B = \left( {0;\,\, + \infty } \right)\). Tập hợp \(A \cap B\) là
\(\left[ { - 2;\,\, + \infty } \right)\);
\(\left( {0;\,\,3} \right]\);
\(\left[ {0;\,\,3} \right]\);
\(\left( {0;\,\,3} \right)\).
Cho tập hợp \(A = \left\{ {x \in \mathbb{R}| - 8 \le x < 2} \right\}\). Viết tập hợp \(A\) dưới dạng kí hiệu đoạn, khoảng hoặc nửa khoảng ta được
\(A = \left\{ { - 8;\,\,2} \right\}\);
\(A = \left( { - 8;\,\,2} \right)\);
\(A = \left[ { - 8;\,\,2} \right]\);
\(A = \left[ { - 8;\,\,2} \right)\).
Hình nào sau đây minh họa \[A\] là tập con của \[B\]?
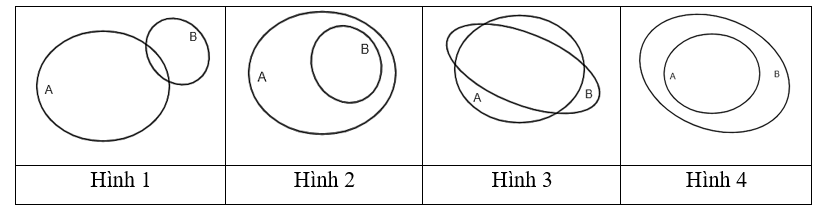
Hình 1;
Hình 2;
Hình 3;
Hình 4.
Hai vectơ được gọi là bằng nhau nếu
chúng có cùng hướng và cùng độ dài;
chúng có hướng ngược nhau và cùng độ dài;
chúng có cùng độ dài;
chúng có cùng phương và cùng độ dài.
Miền nghiệm của bất phương trình bậc nhất hai ẩn \(x + 5y > 2\) là
nửa mặt phẳng bờ là đường thẳng \(d:x + 5y = 2\) chứa gốc tọa độ \(O\left( {0;\,\,0} \right)\) (kể cả bờ \(d\));
nửa mặt phẳng bờ là đường thẳng \(d:x + 5y = 2\) không chứa gốc tọa độ \(O\left( {0;\,\,0} \right)\) (kể cả bờ \(d\));
mửa mặt phẳng bờ là đường thẳng \(d:x + 5y = 2\) chứa gốc tọa độ \(O\left( {0;\,\,0} \right)\) (không kể bờ \(d\));
nửa mặt phẳng bờ là đường thẳng \(d:x + 5y = 2\) không chứa gốc tọa độ \(O\left( {0;\,\,0} \right)\) (không kể bờ \(d\)).
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
\({x^2} + 3{y^2} \ge 9\);
\({3^3}x + {4^2}y > 25\);
\(\frac{2}{x} + \frac{3}{y} < 5\);
\( - xy + {3^2}y < 0\).
Điểm \[A\left( { - 1;\,3} \right)\] là điểm thuộc miền nghiệm của bất phương trình
\[ - 3x + 2y - 4 > 0\];
\[x + 3y < 0\];
\[3x - y > 0\];
\[2x - y + 4 > 0\].
Hệ bất phương trình nào là hệ bất phương trình bậc nhất hai ẩn?
\(\left\{ \begin{array}{l}x + 5{y^2} \ge 1\\ - x + y < 2\end{array} \right.\);
\(\left\{ \begin{array}{l}x{y^2} < 1\\x + 2y > - 4\end{array} \right.\);
\(\left\{ \begin{array}{l}\frac{1}{{3x}} + \frac{1}{y} > 1\\\frac{2}{x} + y > 3\end{array} \right.\);
\(\left\{ \begin{array}{l}x + 2y < 1\\{5^2}x + 7y > 2\end{array} \right.\).
Cặp số nào sau đây là một nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x - y \le 2\\2x + y < 8\\ - x + 3y \ge 6\end{array} \right.\)?
\(\left( {2;\, - 3} \right)\);
\(\left( {4;\,\,1} \right)\);
\(\left( { - 2;\,\, - 2} \right)\);
\(\left( { - 1;\,\,5} \right)\).
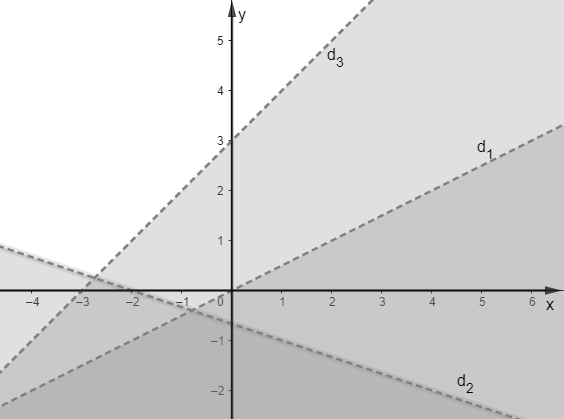
Miền nghiệm của hệ bất phương trình \[\left\{ \begin{array}{l}x - 2y < 0\\x + 3y > - 2\\y - x < 3\end{array} \right.\] là phần không tô đậm của hình vẽ nào trong các hình vẽ sau?
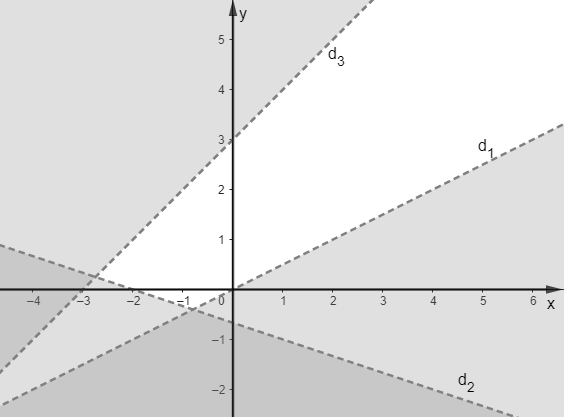
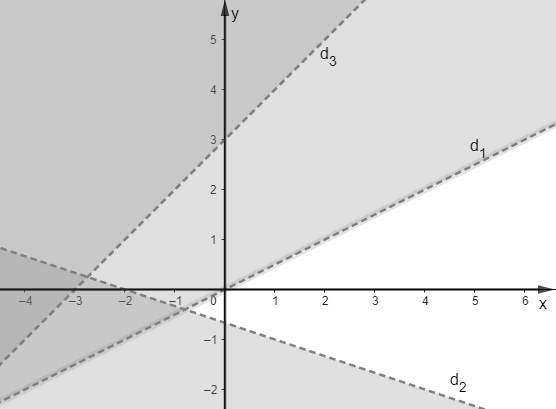
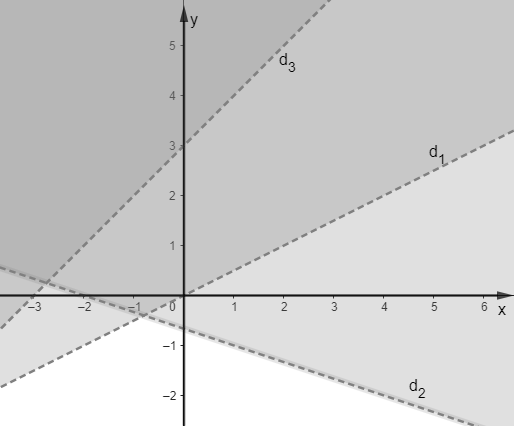
Cho \[\alpha \] là góc tù. Khẳng định nào sau đây là sai?
\[\cos \alpha < 0\];
\[\sin \alpha < 0\];
\[\tan \alpha < 0\];
\[\cot \alpha < 0\].
Cho tam giác \(ABC\) với \(BC = a,\,\,AC = b,\,\,AB = c\). Khẳng định nào sau đây là sai?
\({a^2} = {b^2} + {c^2} - 2bc \cdot \cos A\);
\({a^2} = {b^2} + {c^2}\);
\({b^2} = {c^2} + {a^2} - 2ca \cdot \cos B\);
\({c^2} = {b^2} + {a^2} - 2ba \cdot \cos C\).
Cho góc \(\alpha \) và \(\beta \) thỏa mãn \(\tan \alpha = \cot \beta \). Mối liên hệ của hai góc đó là
\(\alpha \) và \(\beta \) bù nhau;
\(\alpha \) và \(\beta \) phụ nhau;
\(\alpha \) và \(\beta \) bằng nhau;
\(\alpha \) và \(\beta \) không có mối liên hệ.
Giá trị của biểu thức \[P = \cos 30^\circ .\cos 60^\circ - \sin 30^\circ .\sin 60^\circ \] là?
\[P = \sqrt 3 \];
\[P = \frac{{\sqrt 3 }}{2}\];
\[P = 1\];
\[P = 0\].
Cho tam giác \(ABC\) nội tiếp đường tròn có bán kính \(R = 12\) và\(\,\widehat C = 30^\circ \). Độ dài cạnh \(AB\) bằng
6;
12;
\(12\sqrt 3 \);
24.
Cho tam giác \(ABC\) có \[AB = 10,\,\,\widehat C = 45^\circ ,\,\,\widehat B = 60^\circ \]. Độ dài cạnh \(AC\) là
\(5\sqrt 3 \);
\(5\sqrt 6 \);
\(10\sqrt 3 \);
\(10\sqrt 6 \).
Trên sườn đồi, với độ dốc \[12\% \] (độ dốc của sườn đồi được tính bằng tan góc nhọn tạo bởi sườn đồi với phương ngang) có một cây cao mọc thẳng đứng. Ở phía chân đồi, cách gốc cây \[30\]m, người ta nhìn ngọn cây dưới một góc \[45^\circ \] so với phương ngang. Hỏi chiều cao của cây là bao nhiêu (làm tròn đến hàng đơn vị, theo đơn vị mét)?
\[26\];
\[30\];
\[6\];
\[15\].
Cho tam giác \(ABC\) có \(AB = 2,\,\,AC = 2\sqrt 2 ,\,\cos \left( {B + C} \right) = - \frac{{\sqrt 2 }}{2}\). Độ dài cạnh \(BC\) là
2;
4;
12;
20.
Cho lục giác đều \(ABCDEF\) có tâm \(O\). Số các vectơ khác vectơ-không, ngược hướng với vectơ \(\overrightarrow {OA} \), có điểm đầu và điểm cuối là các đỉnh của lục giác đều là
2;
3;
4;
6.
Cho 2 vectơ \[\overrightarrow x ,\,\overrightarrow y \]. Mệnh đề nào sau đây đúng?
Nếu 2 vectơ \[\overrightarrow x ,\,\overrightarrow y \] cùng phương thì chúng cùng hướng.
Nếu 2 vectơ \[\overrightarrow x ,\,\overrightarrow y \] cùng hướng thì chúng cùng phương;
Nếu 2 vectơ \[\overrightarrow x ,\,\overrightarrow y \] bằng nhau thì chúng ngược hướng;
Nếu 2 vectơ \[\overrightarrow x ,\,\overrightarrow y \] đối nhau thì chúng cùng hướng.
II. PHẦN TỰ LUẬN (3 ĐIỂM)
(1,0 điểm) Cho 2 tập hợp \[A = \left[ { - 3;\,6} \right],\,B = \left[ {2m - 4;\,2m + 3} \right)\].
a) Tìm tập hợp \[A \cap \mathbb{Z}\].
b) Tìm \[m\] để \[A \cap B = \emptyset \].
(1 điểm) Một công ty điện tử sản xuất hai kiểu radio trên hai dây chuyền độc lập. Radio kiểu một sản xuất trên dây chuyền một với công suất 45 radio/ngày, radio kiểu hai sản xuất trên dây chuyền hai với công suất 80 radio/ngày. Để sản xuất một chiếc radio kiểu một cần 12 linh kiện, để sản xuất một chiếc radio kiểu hai cần 9 linh kiện. Tiền lãi khi bán một chiếc radio kiểu một là 250 000 đồng, lãi thu được khi bán một chiếc radio kiểu hai là 180 000 đồng. Hỏi cần sản xuất như thế nào để tiền lãi thu được là nhiều nhất, biết rằng số linh kiện có thể sử dụng tối đa trong một ngày là 900 ?
(1,0 điểm) Khu vườn nhà anh T có dạng miền tứ giác \[ABCD\] với các kích thước đo đạc được ghi trên hình vẽ bên dưới:
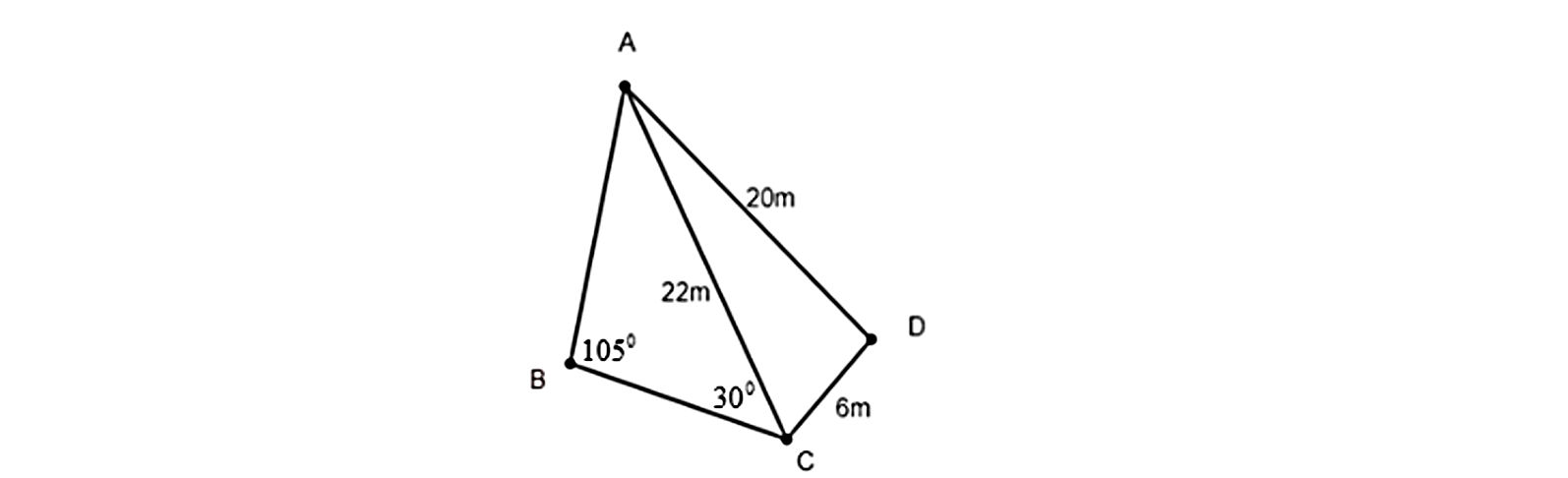
a) Tính khoảng cách từ điểm \[A\] đến điểm \[B\] (kết quả làm tròn một chữ số thập phân).
b) Tính diện tích khu vườn đó (kết quả làm tròn một chữ số thập phân).








