Bộ 5 đề thi cuối kì 1 Toán 10 Cánh diều cấu trúc mới có đáp án - Đề 02
22 câu hỏi
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Trong các câu sau có bao nhiêu câu là mệnh đề:
(1): Số 3 là một số chẵn.
(2): \(2x + 1 = 3\).
(3): Các em hãy cố gắng làm bài thi cho tốt.
(4): \(1 < 3 \Rightarrow 4 < 2\).
2.
3.
1.
4.
Cho tập hợp \(A = \left\{ {x + 1|x \in \mathbb{N},x \le 5} \right\}\). Tập hợp A là:
\(A = \left\{ {1;2;3;4;5} \right\}\).
\(A = \left\{ {0;1;2;3;4;5;6} \right\}\).
\(A = \left\{ {0;1;2;3;4;5} \right\}\).
\(A = \left\{ {1;2;3;4;5;6} \right\}\).
Cho tập hợp \(A = \left\{ {1;2;3;4} \right\},B = \left\{ {0;2;4;6} \right\}\). Mệnh đề nào sau đây là đúng?
\(A \cap B = \left\{ {2;4} \right\}\).
\(A \cup B = \left\{ {0;1;2;3;4;5;6} \right\}\).
\(A \subset B\).
\(A\backslash B = \left\{ {0;6} \right\}\).
Cho 2 tập hợp \[A = \left\{ {\left. {x \in \mathbb{Z}} \right|{x^2} + x - 6 = 0} \right\}\], \[B = \left\{ {\left. {x \in \mathbb{N}} \right|2{x^2} - 3x + 1 = 0} \right\}\]. Chọn khẳng định đúng?
\[B\backslash A = \left\{ {1\,;2} \right\}\].
\[A \cap B = \left\{ { - 3\,;1\,;2} \right\}\].
\[A\backslash B = A\].
\[A \cup B = \emptyset \].
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
\(2{x^2} + 3y > 0\).
\({x^2} + {y^2} < 2\).
\(x + {y^2} \ge 0\).
\(x + y \ge 0\).
Anh A muốn thuê một chiếc ô tô (có người lái) trong một tuần. Giá thuê xe như sau: từ thứ hai đến thứ sáu phí cố định là 900 nghìn đồng/ ngày và phí tính theo quãng đường di chuyển là 10 nghìn đồng/km còn thứ bảy và chủ nhật thì phí cố định là 1200 nghìn đồng/ngày và phí tính theo quãng đường di chuyển là 15 nghìn đồng/km. Gọi \(x,y\) lần lượt là số km mà anh A đi trong các ngày từ thứ hai đến thứ 6 và trong hai ngày cuối tuần. Viết bất phương trình biểu thị mối liên hệ giữa \(x\) và \(y\) sao cho tổng số tiền anh A phải trả không quá 20 triệu đồng.
\[10x + 15y \le 20000\].
\[2x + 3y \ge 2620\].
\[10x + 15y \ge 20000\].
\[2x + 3y \le 2620\].
Bảng biến thiên của hàm số \[y = - 2{x^2} + 4x + 1\] là bảng nào sau đây?
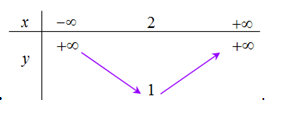
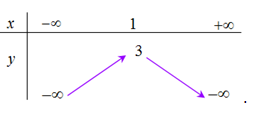
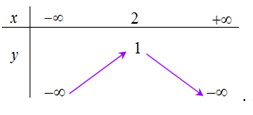
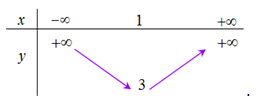
Parabol (P): \(y = 2{x^2} - 4x + 3\) có trục đối xứng là đường thẳng có phương trình là
\[x = 2\].
\[x = - 1\].
\[x = 1\].
\[x = - 2\].
Số thực dương lớn nhất thỏa mãn \[{x^2} - x - 12 \le 0\] là ?
\(1.\)
\(2.\)
\(3.\)
\(4.\)
Tập nghiệm \(S\) của phương trình \(\sqrt {2x - 3} = x - 3\) là
\[S = \left\{ 6 \right\}\].
\[S = \left\{ 2 \right\}\].
\[S = \left\{ {2;6} \right\}\].
\[S = \emptyset \].
Cho \(\Delta ABC\) gọi \(M,N,P\) lần lượt là trung điểm của các cạnh \(AB,AC,BC\). Hỏi \(\overrightarrow {MP} + \overrightarrow {NP} \) bằng vectơ nào?
\(\overrightarrow {AM} \).
\(\overrightarrow {MN} \).
\(\overrightarrow {PB} \).
\(\overrightarrow {AP} \).
Cho tam giác \(ABC\). Lấy điểm \(N\) thuộc cạnh \(BC\) sao cho \(NB = \frac{5}{6}BC\). Hãy phân tích \(\overrightarrow {AN} \) theo các vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \).
\(\overrightarrow {AN} = \frac{1}{3}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} \).
\(\overrightarrow {AN} = \frac{1}{6}\overrightarrow {AB} - \frac{5}{6}\overrightarrow {AC} \).
\(\overrightarrow {AN} = \frac{1}{6}\overrightarrow {AB} + \frac{5}{6}\overrightarrow {AC} \).
\(\overrightarrow {AN} = - \frac{1}{6}\overrightarrow {AB} + \frac{5}{6}\overrightarrow {AC} \).
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Bác Minh có kế hoạch đầu tư không quá 240 triệu đồng vào hai kho X và kho Y. Để đạt được lợi nhuận thì kho Y phải đầu tư ít nhất 40 triệu đồng và số tiền đầu tư cho kho X phải ít nhất gấp ba lần số tiền cho kho Y. Khi đó:
a) Gọi \(x,y\) (đơn vị: triệu đồng) tiền bác Minh đầu tư vào kho X và Y ta có hệ bất phương trình \(\left\{ \begin{array}{l}x + y \le 240\\y \ge 40\\x \ge 3y\end{array} \right.\).
b) Miền nghiệm của hệ bất phương trình tiền bác Minh đầu tư vào kho là một tứ giác.
c) Điểm \(C\left( {200;40} \right)\) không thuộc miền nghiệm của hệ bất phương trình tiền bác Minh đầu tư vào kho.
d) Điểm \(A\left( {180;60} \right)\) là điểm có tung độ lớn nhất thuộc miền nghiệm của hệ bất phương trình tiền bác Minh đầu tư vào kho.
Cho đồ thị hàm số bậc hai \(y = f(x)\) có dạng như hình sau:
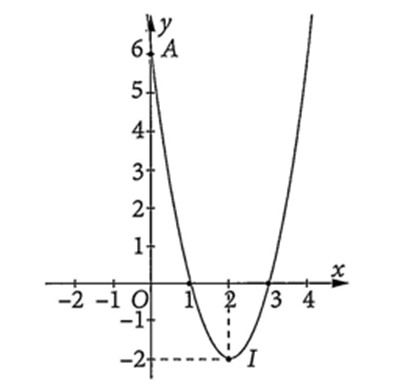
a) Trục đối xứng của đồ thị là đường thẳng \(x = - 2\).
b) Đỉnh \(I\) của đồ thị hàm số có tọa độ là \((2; - 2)\).
c) Đồ thị hàm số đi qua điểm \(A(0;6)\)
d) Hàm số đã cho là \(y = 2{x^2} - 2x + 6\).
Cho \(\Delta ABC\) có \(\widehat A = 135^\circ ,\widehat C = 15^\circ \) và \(b = 12\). Khi đó:
a) \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = \frac{1}{2}R\).
b) \(a = 12\sqrt 2 \).
c) \(c \approx 8,21\).
d) \(R = 15\).
Trong mặt phẳng, cho 3 điểm phân biệt \(A,B,C\).
a) Có 3 vectơ mà điểm đầu và điểm cuối là ba điểm \(A,B,C\).
b) \(\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} = \overrightarrow 0 \) với \(I\) là trọng tâm \(\Delta ABC\).
c) \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {CA} \).
d) \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA} = \overrightarrow 0 \).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời câu 1 đến câu 6.
Một xưởng sản xuất nước mắm, mỗi lít nước mắm loại I cần 3 kg cá và 2 giờ công lao động, đem lại mức lãi là 50000 đồng; mỗi lít nước mắm loại II cần 2 kg cá và 3 giờ công lao động, đem lại mức lãi là 40000 đồng. Xưởng có 230 kg cá và cần làm việc trong 220 giờ. Hỏi xưởng đó nên sản xuất bao nhiêu lít nước mắm loại I để có mức lãi cao nhất?
Bảng giá cước gọi quốc tế của công ty viễn thông A được cho bởi bảng sau:
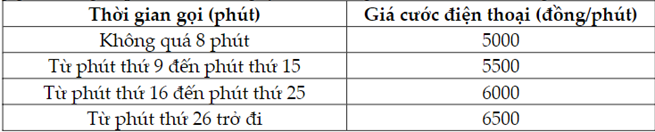
Ông An thực hiện cuộc gọi quốc tế 12 phút. Số tiền ông An phải trả là bao nhiêu đồng?
Một công ty du lịch thông báo giá tiền cho chuyến đi tham quan của một nhóm khách như sau: 50 khách đầu tiên có giá 300000 đồng/người. Nếu có nhiều hơn 50 người đăng kí thì cứ có thêm một người, giá vé sẽ giảm 5000 đồng/người cho toàn bộ hành khách. Biết chi phí thực sự của chuyến đi là 15080000 đồng. Số người của nhóm khách du lịch nhiều nhất là bao nhiêu để công ty không bị lỗ?
Cho \(\Delta ABC\) có \(AB = 8,AC = 5,\widehat {BAC} = 60^\circ \). Tính chiều cao \(AH\) của \(\Delta ABC\) (kết quả làm tròn đến hàng phần trăm).
Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa phụ hai bên như hình vẽ.
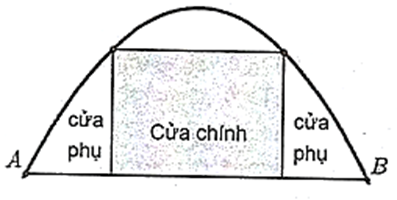
Biết chiều cao cổng parabol là \(4\;{\rm{m}}\), cửa chính (ở giữa parabol) cao \(3\;{\rm{m}}\) và rộng 4 m. Tính khoảng cách giữa hai chân cổng parabol ấy (đoạn \(AB\) trên hình vẽ).
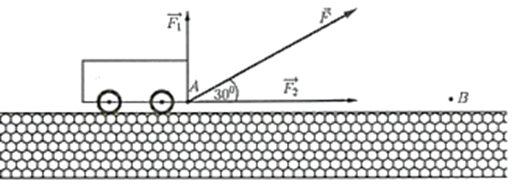
Một chiếc xe được kéo bởi một lực \(\vec F\) có độ lớn \(50\;{\rm{N}}\), di chuyển theo quãng đường từ \(A\) đến \(B\) có chiều dài \(200\;{\rm{m}}\). Cho biết góc hợp bởi lực \(\vec F\) và \(\overrightarrow {AB} \) bằng \(30^\circ \) và lực \(\vec F\) được phân tích thành hai lực \({\vec F_1},{\vec F_2}\). Gọi \(m,n,k\) lần lượt là công sinh ra bởi các lực \(\vec F,{\vec F_1},\overrightarrow {{F_2}} \) . Khi đó tính \(S = m - n - k\).