Bộ 10 đề thi Giữa kì 1 Toán 10 Cánh Diều có đáp án - Đề 9
76 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (7,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:
Góc có số đo \[{108^{\rm{o}}}\]đổi ra radian là
\[\frac{{3\pi }}{5}.\]
\[\frac{\pi }{{10}}.\]
\[\frac{{3\pi }}{2}.\]
\[\frac{\pi }{4}.\]
Chọn công thức sai trong các công thức sau:
\({\sin ^2}\alpha + {\cos ^2}\alpha = 1\).
\(1 + {\tan ^2}\alpha = \frac{1}{{1 - {{\sin }^2}\alpha }}\).
\({\sin ^2}2\alpha + {\cos ^2}2\alpha = 1\)
\(1 + {\cot ^2}\alpha = \frac{1}{{co{s^2}\alpha }}\).
Với mọi góc lượng giác \(a\), \(b\), trong các công thức sau, công thức nào đúng (giả sử rằng tất cả các đẳng thức đều có nghĩa)?
\(\tan \left( {a - b} \right) = \frac{{\tan a + \tan b}}{{1 - \tan a\tan b}}\).
\[\tan \left( {a--b} \right) = \tan a - \tan b\].
\(\tan \left( {a + b} \right) = \frac{{\tan a + \tan b}}{{1 - \tan a\tan b}}\).
\[\tan \left( {a + b} \right) = \tan a + \tan b\].
Cho \[\cos \alpha = \frac{1}{3}\]. Khi đó \[\sin \left( {\frac{\pi }{2} - \alpha } \right)\] bằng
\( - \frac{2}{3}.\)
\[ - \frac{1}{3}.\]
\(\frac{1}{3}.\)
\(\frac{2}{3}.\)
Cho góc lượng giác \(\left( {Ou,Ov} \right)\) có số đo \( - \frac{\pi }{7}\). Trong các số \( - \frac{{29\pi }}{7};\,\,\, - \frac{{22\pi }}{7};\,\,\,\frac{{6\pi }}{7};\,\,\,\frac{{41\pi }}{7}\), những số nào là số đo của một góc lượng giác có cùng tia đầu, tia cuối với góc đã cho?
\( - \frac{{29\pi }}{7};\,\,\,\frac{{41\pi }}{7}\).
\( - \frac{{29\pi }}{7};\,\,\, - \frac{{22\pi }}{7}\).
\( - \frac{{22\pi }}{7};\,\,\,\frac{{41\pi }}{7}\).
\(\frac{{6\pi }}{7};\,\,\,\frac{{41\pi }}{7}\).
Cho \(\sin \alpha = \frac{3}{5}\) và \(\frac{\pi }{2} < \alpha < \pi \). Giá trị của \[{\rm{cos}}\alpha \] là
\(\frac{4}{5}\).
\( - \frac{4}{5}\).
\( \pm \frac{4}{5}\).
\(\frac{{16}}{{25}}\).
Biết góc \[\alpha \] thỏa mãn \[\cos \alpha = \frac{2}{3}\]. Hỏi \[\alpha \] có thể nhận giá trị trong khoảng nào dưới đây?
\[\left( {\frac{\pi }{2},\frac{{2\pi }}{3}} \right)\].
\[\left( {\frac{{8\pi }}{3},\frac{{17\pi }}{6}} \right)\].
\[\left( {\frac{\pi }{4},\frac{\pi }{3}} \right)\].
\[\left( { - \pi ; - \frac{{2\pi }}{3}} \right)\].
Cho góc \(\alpha \) thỏa mãn \(\tan \alpha = 2.\) Giá trị của biểu thức \(P = \frac{{3\sin \alpha - 2\cos \alpha }}{{5\cos \alpha + 7\sin \alpha }}\) là
\(P = - \frac{4}{9}.\)
\(P = \frac{4}{9}.\)
\(P = - \frac{4}{{19}}.\)
\(P = \frac{4}{{19}}.\)
Khẳng định nào sau đây là đúng về hàm số \(y = \tan x?\)
Hàm số \(y = \tan x\) có tập xác định là \[\mathbb{R}.\]
Hàm số \(y = \tan x\) có tập giá trị là \[\left[ { - 1;1} \right].\]
Hàm số \(y = \tan x\) có đồ thị đối xứng qua gốc tọa độ.
Hàm số \(y = \tan x\) tuần hoàn với chu kì \(2\pi .\)
Khẳng định nào sau đây là sai?
Hàm số \(y = \sin x\) đồng biến trên khoảng \[\left( {0;\frac{\pi }{2}} \right).\]
Hàm số \(y = \sin x\) nghịch biến trên khoảng \(\left( { - 3\pi ; - \frac{{5\pi }}{2}} \right).\)
Hàm số \(y = \cos x\) đồng biến trên khoảng \(\left( { - \pi ;0} \right).\)
Hàm số \(y = \cos x\) nghịch biến trên khoảng \(\left( {\frac{{3\pi }}{2};\frac{{5\pi }}{2}} \right).\)
Cho các khẳng định sau:
(1) Hàm số \(y = f\left( x \right)\) có tập xác định \(D\) được gọi là tuần hoàn nếu tồn tại một số \(T\) khác \(0\) sao cho với mọi \(x \in D\) ta có \(f\left( {x + T} \right) = f\left( x \right).\)
(2) Hàm số \(y = f\left( x \right)\) có tập xác định \(D\) được gọi là hàm số chẵn nếu \(\forall x \in D\) thì \( - x \in D\) và \(f\left( { - x} \right) = - f\left( x \right)\).
(3) Hàm số \(y = f\left( x \right)\) có tập xác định \(D\) được gọi là hàm số lẻ nếu \(\forall x \in D\) thì \( - x \in D\) và \(f\left( { - x} \right) = f\left( x \right).\)
Có bao nhiêu khẳng định đúng trong các khẳng định trên?
0.
1.
2.
3.
Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D:
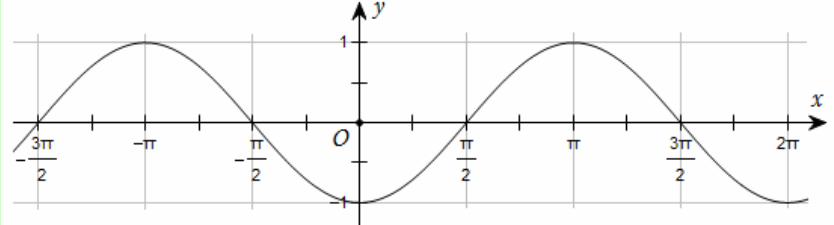
Hỏi hàm số đó là hàm số nào?
\(y = \cos x\).
\(y = - \cos x\).
\(y = \cos \left| x \right|\).
\(y = \left| {\cos x} \right|\).
Cho hàm số \(f\left( x \right) = \sin 2x\) và \(g\left( x \right) = {\tan ^2}x.\) Khẳng định nào sau đây là đúng?
\(f\left( x \right)\) là hàm số chẵn, \(g\left( x \right)\) là hàm số lẻ.
\(f\left( x \right)\) là hàm số lẻ, \(g\left( x \right)\) là hàm số chẵn.
\(f\left( x \right)\) là hàm số chẵn, \(g\left( x \right)\) là hàm số chẵn.
\(f\left( x \right)\) và \(g\left( x \right)\) đều là hàm số lẻ.
Hàm số \(y = 5 + 4\sin 2x\cos 2x\) có tất cả bao nhiêu giá trị nguyên?
\(3.\)
\(4.\)
\(5.\)
\(6.\)
Tất cả các nghiệm của phương trình \(\sin x = \sin \frac{\pi }{3}\) là
\(\left[ \begin{array}{l}x = \frac{\pi }{3} + k2\pi \\x = - \frac{\pi }{3} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right).\)
\(\left[ \begin{array}{l}x = \frac{\pi }{3} + k2\pi \\x = \frac{{2\pi }}{3} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right).\)
\(x = \frac{\pi }{3} + 2\pi \,\,\left( {k \in \mathbb{Z}} \right).\)
\(\left[ \begin{array}{l}x = \frac{\pi }{3} + k\pi \\x = \frac{{2\pi }}{3} + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right).\)
Phương trình nào dưới đây vô nghiệm?
\(\sin x + 5 = 0.\)
\(2\sin x - \sin x - 1 = 0.\)
\(\tan x + 5 = 0\).
\(3\cos x - 1 = 0.\)
Một phương trình tương đương với phương trình \(\sin 4x\cos 2x = \sin x\cos 5x\) là
\(\sin 4x + \sin 2x = 0.\)
\(\sin 4x = \sin 2x.\)
\(\sin 4x = \sin 5x.\)
\(\sin 4x = \sin x.\)
Nếu \[\cos \left( {a + b} \right) = 0\] thì khẳng định nào sau đây đúng?
\[\left| {\sin \left( {a + 2b} \right)} \right| = \left| {\sin a} \right|.\]
\[\left| {\sin \left( {a + 2b} \right)} \right| = \left| {\sin b} \right|.\]
\[\left| {\sin \left( {a + 2b} \right)} \right| = \left| {\cos a} \right|.\]
\[\left| {\sin \left( {a + 2b} \right)} \right| = \left| {\cos b} \right|.\]
Biểu diễn họ nghiệm của phương trình \(\sin 2x = 1\) trên đường tròn đơn vị ta được bao nhiêu điểm?
\(1\).
\(8\).
\(4\).
\(2\).
Giải phương trình lượng giác: \(2\cos \frac{x}{2} + \sqrt 3 = 0\) có nghiệm là
\(x = \pm \frac{{5\pi }}{3} + k2\pi \).
\(x = \pm \frac{{5\pi }}{6} + k2\pi \).
\(x = \pm \frac{{5\pi }}{6} + k4\pi \).
\(x = \pm \frac{{5\pi }}{3} + k4\pi \).
Cho dãy số \(\left( {{u_n}} \right)\), biết \(\left\{ \begin{array}{l}{u_1} = - 1\\{u_{n + 1}} = {u_n} + 3\end{array} \right.\)với \(n \ge 0\). Ba số hạng đầu tiên của dãy số đó là lần lượt là những số nào dưới đây?
\( - 1;{\mkern 1mu} 2;{\mkern 1mu} 5.\)
\(1;{\mkern 1mu} 4;{\mkern 1mu} 7.\)
\(4;{\mkern 1mu} 7;{\mkern 1mu} 10.\)
\(\;\; - 1;3;7.\)
Cho dãy số \(\left( {{u_n}} \right)\), biết \({u_n} = {3^n}.\) Số hạng \({u_{2n - 1}}\) là
\({u_{2n - 1}} = {3^2}{.3^n} - 1.\)
\({u_{2n - 1}} = {3^n}{.3^{n - 1}}.\)
\({u_{2n - 1}} = {3^{2n}} - 1.\)
\({u_{2n - 1}} = {3^{2\left( {n - 1} \right)}}.\)
Cho dãy số \[\left( {{u_n}} \right),\] được xác định \[\left\{ \begin{array}{l}{u_1} = 2\\{u_{n + 1}} - {u_n} = 2n - 1\end{array} \right..\] Số hạng tổng quát \[{u_n}\] của dãy số là số hạng nào dưới đây?
\[{u_n} = 2 + {\left( {n - 1} \right)^2}.\]
\[{u_n} = 2 + {n^2}.\]
\[{u_n} = 2 + {\left( {n + 1} \right)^2}.\]
\[{u_n} = 2 - {\left( {n - 1} \right)^2}.\]
Mệnh đề nào sau đây đúng?
Dãy số \({u_n} = \frac{1}{n} - 2\) là dãy tăng.
Dãy số \({u_n} = {\left( { - 1} \right)^n}\left( {{2^n} + 1} \right)\) là dãy giảm.
Dãy số \({u_n} = \frac{{n - 1}}{{n + 1}}\) là dãy giảm.
Dãy số \({u_n} = 2n + \cos \frac{1}{n}\) là dãy tăng.
Trong các dãy số \[\left( {{u_n}} \right)\] cho bởi số hạng tổng quát \[{u_n}\] sau, dãy số nào bị chặn?
\[{u_n} = \frac{1}{{{2^n}}}.\]
\[{u_n} = {3^n}.\]
\[{u_n} = \sqrt {n + 1} .\]
\[{u_n} = {n^2}.\]
Trong không gian, cho 4 điểm không đồng phẳng. Có thể xác định được bao nhiêu mặt phẳng phân biệt từ các điểm đã cho?
\[6.\]
\(4.\)
\(3.\)
\(2.\)
Trong các khẳng định sau, khẳng định nào đúng?
Nếu 3 điểm \(A,\;B,\;C\) là 3 điểm chung của 2 mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) thì \(A,\;B,\;C\) thẳng hàng\(.\)
Nếu \(A,\;B,\;C\) thẳng hàng và \(\left( P \right)\), \(\left( Q \right)\) có điểm chung là \(A\) thì \(B,\;C\) cũng là 2 điểm chung của \(\left( P \right)\) và \(\left( Q \right)\)\(.\)
Nếu 3 điểm \(A,\;B,\;C\) là 3 điểm chung của 2 mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) phân biệt thì \(A,\;B,\;C\) không thẳng hàng\(.\)
Nếu\(A,\;B,\;C\) thẳng hàng và\(A,\;B\) là 2 điểm chung của \(\left( P \right)\) và \(\left( Q \right)\) thì \(C\)cũng là điểm chung của \(\left( P \right)\)và \(\left( Q \right)\)\(.\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang với \(AB\parallel CD\). Gọi \(I\) là giao điểm của \(AC\) và \(BD\). Trên cạnh \(SB\) lấy điểm \(M\). Giao tuyến của hai mặt phẳng \(\left( {ADM} \right)\) và \(\left( {SAC} \right)\) là
\(SI.\)
\(AE\) (\(E\) là giao điểm của \(DM\) và \(SI).\)
\(DM.\)
\(DE\) (\(E\) là giao điểm của \(DM\) và \(SI).\)
Cho bốn điểm \(N\) không cùng ở trong một mặt phẳng. Gọi \(P\) lần lượt là trung điểm của \(D\). Trên \(MND\) lấy điểm \(MND\) sao cho \(MN = \frac{{AB}}{2} = a\) không song song với \(DM = DN = \frac{{AD\sqrt 3 }}{2} = a\sqrt 3 \) (\(MND\) không trùng với các đầu mút). Gọi \(E\) là giao điểm của đường thẳng \(D\) với mặt phẳng \(H\). Mệnh đề nào sau đây đúng?
\(E\) nằm ngoài đoạn \(BC\) về phía \(B.\)
\(E\) nằm ngoài đoạn \(BC\) về phía \(C.\)
\(E\) nằm trong đoạn \(BC.\)
\(E\) nằm trong đoạn \(BC\) và \(E \ne B,{\rm{ }}E \ne C.\)
Cho hai đường thẳng chéo nhau \(a\) và \(b\). Lấy \(A,\;B\) thuộc \(a\) và \(C,\;D\) thuộc \(b.\) Khẳng định nào sau đây đúng khi nói về hai đường thẳng \(AD\) và \(BC\)?
Có thể song song hoặc cắt nhau.
Cắt nhau.
Song song với nhau.
Chéo nhau.
Trong không gian, cho ba đường thẳng phân biệt \(a,\;b,\;c\) trong đó \(a\,\parallel \,b\). Khẳng định nào sau đây sai?
Nếu \[a\,{\rm{//}}\,c\] thì \[b\,\,{\rm{//}}\,c\].
Nếu \(c\) cắt \(a\) thì \(c\) cắt \(b\).
Nếu \(A \in a\) và \(B \in b\) thì ba đường thẳng \(a,\;b,\;AB\) cùng ở trên một mặt phẳng.
Tồn tại duy nhất một mặt phẳng qua \(a\) và \(b\).
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình thang với đáy lớn \[AB\] đáy nhỏ \[CD.\] Gọi \[M,\,\,N\] lần lượt là trung điểm của \[SA\] và \[SB.\] Gọi \[P\] là giao điểm của \[SC\] và \[\left( {AND} \right).\] Gọi \(I\) là giao điểm của \[AN\] và \[DP.\] Hỏi tứ giác \[SABI\] là hình gì?
Hình bình hành.
Hình chữ nhật.
Hình vuông.
Hình thoi.
Gọi \(G\) là trọng tâm tứ diện \(ABCD.\) Gọi \(A'\) là trọng tâm của tam giác \[BCD\,.\] Tỉ số \[\frac{{GA}}{{GA'}}\] bằng
\(2\,.\)
\(3.\)
\(\frac{1}{3}.\)
\(\frac{1}{2}.\)
Cho hai đường thẳng phân biệt \(a,\;b\) và mặt phẳng\(\left( \alpha \right)\). Giả sử \[a\,{\rm{//}}\,\,b,\]\(b\,{\rm{//}}\,\left( \alpha \right).\) Khi đó:
\[a\,\,{\rm{//}}\,\,\left( \alpha \right).\]
\[a \subset \left( \alpha \right).\]
\(a\) cắt \[\left( \alpha \right).\]
\[a\,\,{\rm{//}}\,\,\left( \alpha \right)\] hoặc \[a \subset \left( \alpha \right).\]
Cho hai hình bình hành \[ABCD\] và \[ABEF\] không cùng nằm trong một mặt phẳng. Gọi \[O,\,\,{O_1}\] lần lượt là tâm của \[ABCD,\,\,ABEF\,.\]\[M\] là trung điểm của \[CD\,.\] Khẳng định nào sau đây sai?
\(O{O_1}\,{\rm{//}}\,\left( {BEC} \right).\)
\[O{O_1}\,{\rm{//}}\,\left( {AFD} \right).\]
\[O{O_1}\,{\rm{//}}\,\left( {EFM} \right).\]
\[M{O_1}\] cắt \[\left( {BEC} \right).\]
PHẦN II. TỰ LUẬN (3,0 điểm)
(1,5 điểm)
a) Cho góc \(\alpha \) thỏa mãn \[\cos \alpha = - \frac{4}{5}\] và \[\pi < \alpha < \frac{{3\pi }}{2}.\] Tính \[P = \sin \frac{\alpha }{2}.\cos \frac{{3\alpha }}{2}.\]
b) Giải phương trình \[\cos 2\left( {x + \frac{\pi }{3}} \right) + 4\cos \left( {\frac{\pi }{6} - x} \right) = \frac{5}{2}.\]
c) Phương trình của một sóng cơ học có dạng \(u\left( {x,t} \right) = A\cos \left[ {\omega \left( {t - \frac{x}{v}} \right)} \right]\) trong đó \(A\) là biên độ sóng, \(\omega \) là tần số góc của sóng và \(v\) là tốc độ truyền sóng. Biết hai sóng lan truyền theo cùng một chiều trên cùng một sợi dây kéo căng có cùng tần số, cùng biên độ \(10\left( {mm} \right)\) và hiệu số pha là \(\frac{\pi }{2}\). Hãy lập phương trình của sóng tổng hợp?
(0,5 điểm) Xét tính tăng giảm của dãy số \(\left( {{u_n}} \right)\) với \({u_n} = n - \sqrt {{n^2} - 1} .\)
(1,0 điểm)
a) Cho hình chóp \(S.ABCD\). Gọi \(M\), \(N\) lần lượt là trung điểm của \(AB\) và \(BC;\)\(G,\)\(G'\) lần lượt là trọng tâm các tam giác \(SAB\) và \(SBC\). Chứng minh \(GG'\,{\rm{//}}\,\left( {SAC} \right)\).
b) Cho hình chóp \(S.ABCD\) có đáy là hình thang với \(AD\,{\rm{//}}\,BC\). Gọi \(G\) là trọng tâm của tam giác \(SAD;\)\(E\) là điểm thuộc đoạn \(AC\) sao cho \(EC = xEA,\,\,\left( {x > 0} \right)\). Tìm \(x\) để \(GE\,{\rm{//}}\,\left( {SBC} \right)\).
PHẦN I. TRẮC NGHIỆM (7 điểm)
Phát biểu nào sau đây là mệnh đề?
Dịch covid thật khủng khiếp!;
Số \(3\) là số may mắn của tôi;
Trái Đất là một hành tinh trong hệ mặt trời;
Hố đen vũ trụ thật bí ẩn.
Cho mệnh đề .Tìm mệnh đề phủ định của mệnh đề \(P\).
;
;
;
.
Cho các mệnh đề sau đây:
\[\left( I \right):\] Nếu tam giác \(ABC\) đều thì \(AB = AC.\)
\[\left( {II} \right):\] Nếu \(a + b\) là số chẵn thì \(a\) và \(b\) là các số chẵn.
\[\left( {III} \right):\] Nếu tam giác \(ABC\) có tổng hai góc bằng \(90^\circ \) thì tam giác \(ABC\) vuông cân.
Trong các mệnh đề trên, có bao nhiêu mệnh đề đúng?
0.
3.
2.
\(1\).
Cho \[A = \left( { - 5;\,1} \right];\,B = \left[ {3;\, + \infty } \right);\,C = \left( { - \infty ;\, - 2} \right)\]. Câu nào sau đây đúng?
\[A \cup B = \left( { - 5;\, + \infty } \right)\];
\[B \cup C = \left( { - \infty ;\, + \infty } \right)\];
\[B \cap C = \emptyset \];
\[A \cap C = \left[ { - 5;\, - 2} \right]\].
Tập hợp \[A = \left\{ {x \in \mathbb{R}\left| { - 2 \le x < 11} \right.} \right\}\] bằng tập hợp nào dưới đây?
\[A = \left[ { - 2\,;\,11} \right)\];
\[A = \left[ { - 2\,;\,10} \right]\];
\[A = \left\{ { - 2; - 1;0;1;2;3;4;5;6;7;8;9;10} \right\}\];
\[A = \left( { - 2\,;\,11} \right]\].
Cho hai tập hợp \(M = \left\{ {x \in \mathbb{Z},\left| {x - 1} \right| - 5 \le 1} \right\}\). Có bao nhiêu số nguyên thuộc tập hợp \(M\)?
\(8\);
\(14\);
Vô số;
\(7\).
Cho \(x\) là một phần tử của tập hợp \(A\). Cách viết nào sau đây là đúng?
\(x \subset A\);
\(\left\{ x \right\} \in A\);
\(x \in A\);
\(A \subset \left\{ x \right\}\).
Gọi \(M\) là giá trị lớn nhất và \(m\) là giá trị nhỏ nhất của biểu thức \(F\left( {x;\,y} \right) = 4x - 3y\) trên miền nghiệm của hệ bất phương trình: \(\left\{ \begin{array}{l}x + y \ge 3\\x - y \le 5\\y \le 5\end{array} \right.\) được biểu diễn bởi hình vẽ sau:
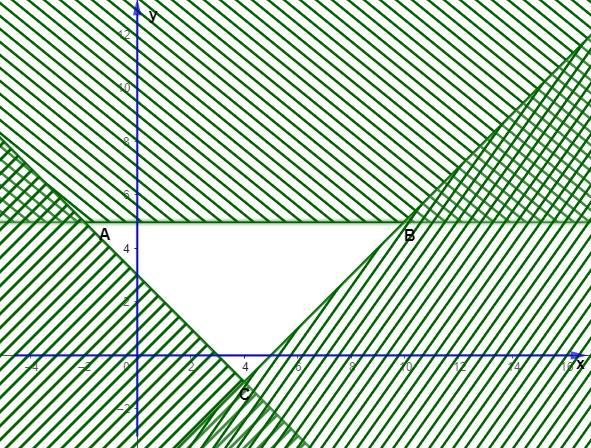
Giá trị \(M - m\) bằng
\(2\);
\(4\);
\(48\);
\(25\).
Bất phương trình nào là bất phương trình bậc nhất hai ẩn?
\(x - {12^2}y > 7\);
\(3x + 4{y^2} \le 7\);
\(\frac{2}{x} - 7y > 90\)
\(xy \ge - 9\).
Trong các hình dưới đây, hình nào biểu diễn miền nghiệm của bất phương trình \(\frac{1}{2}x - 3y \ge - 3\)?
A. 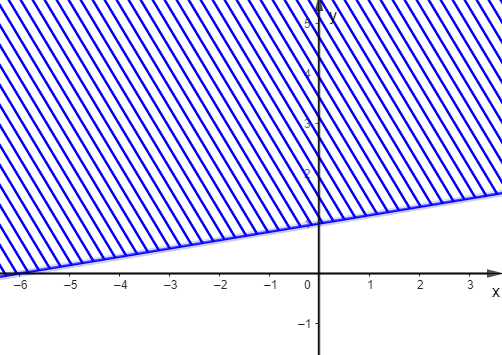 ;
;
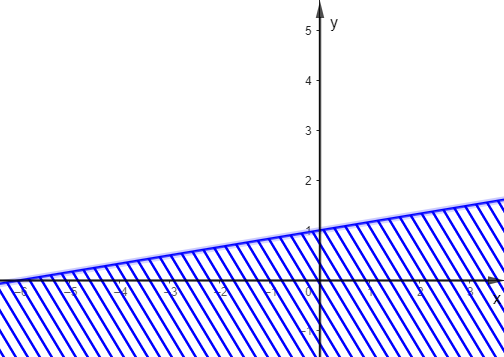
C. 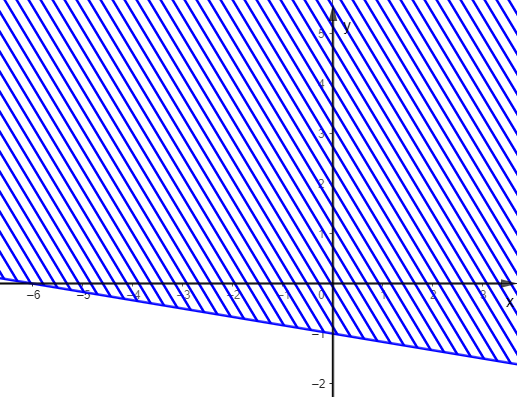 ;
;
D. 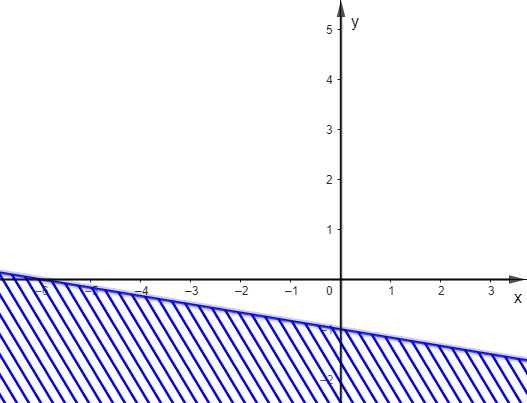 .
.
Cho bất phương trình bậc nhất hai ẩn: \(3mx - y < m + 1\). Với giá trị nào của tham số \(m\) thỏa mãn cặp \(\left( {0;\,\, - 2} \right)\) là nghiệm của bất phương trình đã cho?
\(m = \frac{5}{4}\);
\(m = - \frac{1}{2}\);
\(m = 2\frac{1}{4}\);
\(m = 1\).
Cho hệ bất phương trình \(\left\{ \begin{array}{l}x + y < 0\\y \ge 0\\x \ge - 1\end{array} \right.\). Điểm \(M\left( {{x_0};\,\,{y_0}} \right)\) là điểm thỏa mãn miền nghiệm của hệ bất phương trình trên. Khi đó biểu thức nào dưới đây là đúng?
\({x_0} + {y_0} \ge 0\);
\({x_0} < 0\);
\({y_0} \ge - 1\);
\({x_0} - {y_0} > - 1\).
Cho hệ bất phương trình \(\left\{ \begin{array}{l}x - y < 1\\x + 2y \ge 0\end{array} \right.\) có miền nghiệm được biểu diễn như hình vẽ: 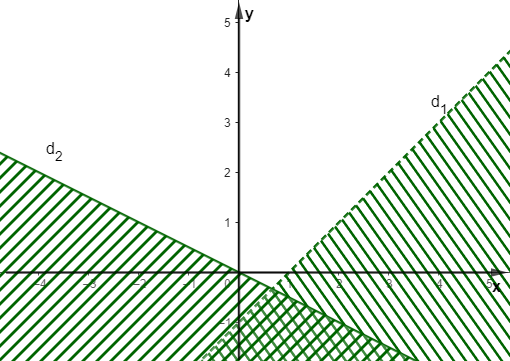
Câu nào mô tả đúng nhất miền nghiệm của hệ bất phương trình trên?
Miền nghiệm của hệ bất phương trình là miền bị gạch chéo trong hình vẽ kể cả hai đường thẳng \({d_1}\) và \({d_2}\);
Miền nghiệm của hệ bất phương trình là miền bị gạch chéo trong hình vẽ không kể cả hai đường thẳng \({d_1}\) và \({d_2}\);
Miền nghiệm của hệ bất phương trình là miền không bị gạch chéo trong hình vẽ kể đường thẳng \({d_1}\) và không kể đường thẳng \({d_2}\);
Miền nghiệm của hệ bất phương trình là miền không bị gạch chéo trong hình vẽ không kể đường thẳng \({d_1}\) và kể cả đường thẳng \({d_2}\).
Trong các cặp số: \(\left( {0;\,\,0} \right);\,\,\,\left( { - 1;\,\,1} \right);\,\,\left( { - 2;\,\,3} \right)\,;\,\,\left( {4;\,\,1} \right)\) có bao nhiêu cặp số là nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x - 2y \le 1\\2x - y > - 2\end{array} \right.\)?
\(1\);
\(2\);
\(3\);
\(4\).
Xét hai đại lượng \(x,y\) phụ thuộc vào nhau theo hệ thức dưới đây. Trường hợp nào \(y\) không là hàm số của \(x\).
\(x + y = 1\);
\({y^2} = x\);
\(y = 2x + 1\);
\(y = {x^2}\).
Cho hàm số \(f\left( x \right) = 2x - 3\). Kết luận nào sau đây đúng?
\(f\left( 1 \right) = 2\);
Hàm số đồng biến trên \(\mathbb{R}\);
Hàm số nghịch biến trên \(\mathbb{R}\).
Tập xác định của hàm số là \(D = \left( {\frac{3}{2};\, + \infty } \right)\);
Cho hàm số \(y = {x^2} - 2x - 1\). Trục đối xứng của hàm số là:
\(x = 1\);
\(x = - 1\);
\(x = - 2\);
\(x = 2\).
Hàm số \(y = {x^2} - 4x + 1\) có bảng biến thiên là
A. 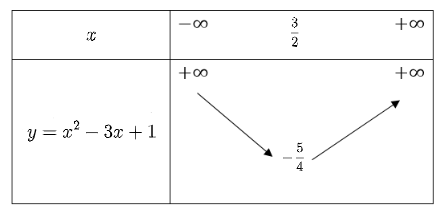
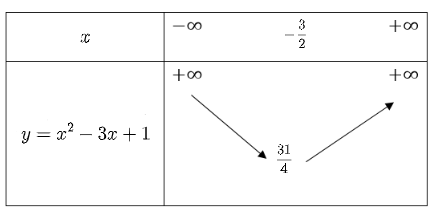
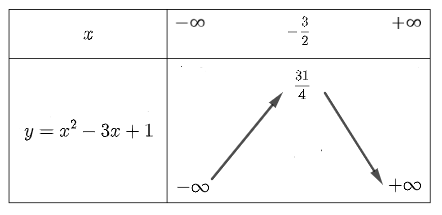
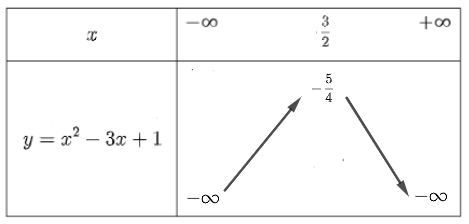
Cho hàm số \[y = a{x^2} + bx + c\,\left( {a \ne 0} \right)\] có đồ thị \[P\] . Tọa độ đỉnh của \[P\] là:
\[I\left( { - \frac{b}{{2a}};\,\frac{\Delta }{{4a}}} \right)\];
\[I\left( { - \frac{b}{a};\, - \frac{\Delta }{{4a}}} \right)\];
\[I\left( { - \frac{b}{{2a}};\, - \frac{\Delta }{{4a}}} \right)\];
\[I\left( {\frac{b}{{2a}};\,\frac{\Delta }{{4a}}} \right)\].
Cho biết \(\cot \alpha = \frac{1}{2}\). Giá trị của \(P = \frac{{2\sin \alpha - 2\cos \alpha }}{{2\cos \alpha + 3\sin \alpha }}\) bằng bao nhiêu?
\(P = 0\);
\(P = \frac{1}{4}\);
\(P = - \frac{1}{4}\);
\(P = \frac{2}{7}\).
Giá trị của biểu thức \(M = \tan \left( { - 10^\circ } \right).\tan 20^\circ ...\tan \left( { - 70^\circ } \right).\tan 80^\circ \) bằng
\(M = - 1\);
\(M = 1\);
\(M = 0\);
\(M = - 4\).
Cho tam giác \(ABC\) có cạnh \(AB = 2cm,\widehat {ABC} = 110^\circ ,\widehat {BAC} = 35^\circ \). Độ dài cạnh \(AC\) nằm trong khoảng nào sau đây?
\(\left( {1;\,\,3} \right)\);
\(\left( {3;\,\,5} \right)\);
\(\left( {5;\,\,7} \right)\);
\(\left( {7;\,\,9} \right)\).
Cho tam giác \(ABC\) vuông tại \(A\). Nhận xét nào dưới đây là sai?
\(\sin \left( {B + C} \right) = \sin A\);
\(\sin B = {\rm{cos}}C\);
\(\tan B = \cot C\);
\(\sin \left( {\frac{{B + C}}{2}} \right) = \sin \frac{A}{2}\).
Tam giác \[ABC\] có diện tích \(S\). Nếu tăng cạnh \(BC\) lên \(2\) lần đồng thời tăng cạnh \(CA\) lên \(3\) lần và giữ nguyên độ lớn của góc \(C\) thì khi đó diện tích của tam giác mới được tạo nên bằng
\(2S\);
\(3S\);
\(4S\);
\(6S\).
Cho tam giác \(ABC\) có \(AB = 5,\,\,BC = 7,\,\,AC = 8\). Chiều cao xuất phát từ đỉnh \(A\) của tam giác \(ABC\) có độ dài là
\(\frac{{5\sqrt 3 }}{2}\);
\(10\sqrt 3 \);
\(\frac{{20\sqrt 3 }}{7}\);
\(\frac{{10\sqrt 3 }}{7}\).
Trong tam giác \(ABC\), phát biểu nào sau đây đúng?
\(\frac{{a + b + c}}{S} = r\);
\(\frac{S}{{a + b + c}} = r\);
\[\frac{S}{{2\left( {a + b + c} \right)}} = r\];
\(\frac{{2S}}{{a + b + c}} = r\).
Hai chiếc tàu thuỷ cùng xuất phát từ \(A\) đi thẳng theo hai hướng tạo với nhau một góc 60°. Tàu thứ nhất chạy với tốc độ 30 km/h. Tàu thứ hai đi với vận tốc 40km/h. Hỏi sau 2h hai tàu cách nhau bao nhiêu km?
\(13\);
\(15\);
\(10\sqrt {13} \);
\(20\sqrt {13} \).
Có bao nhiêu vectơ khác vectơ không được xác định từ hai điểm \(A,B\) bất kỳ
\(1\);
\(2\);
\(0\);
\(4\).
Khẳng định nào sau đây đúng?
Hai vectơ cùng phương nếu giá của chúng song song hoặc trùng nhau;
Hai vectơ được gọi là bằng nhau nếu độ dài của chúng bằng nhau;
Giá của vectơ là đường thẳng vuông góc với vectơ đó;
Vectơ không là vectơ có độ dài bằng mọi vectơ.
Cho hình thoi tâm \(O\), cạnh bằng \(a\) và \(\widehat A = 60^\circ \). Kết luận nào sau đây là đúng?
\(\left| {\overrightarrow {AO} } \right| = \frac{{a\sqrt 3 }}{2}\)
\(\left| {\overrightarrow {OA} } \right| = a\)
\(\left| {\overrightarrow {OA} } \right| = \left| {\overrightarrow {OB} } \right|\)
\(\left| {\overrightarrow {OA} } \right| = \frac{{a\sqrt 2 }}{2}\)
Cho ba điểm \(A,\,B,\,C\) bất kỳ. Kết luận nào sau đây sai?
\(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {CB} \);
\(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \);
\(\overrightarrow {BA} + \overrightarrow {AC} = \overrightarrow {BC} \);
\(\overrightarrow {AB} - \overrightarrow {AC} = \overrightarrow {BC} \).
Cho tam giác \(ABC\). Gọi \(M,\,N,\,P\) lần lượt là trung điểm của \(AB,\,BC,\,CA\). Khi đó \(\overrightarrow {MP} + \overrightarrow {NP} \) bằng
\(\overrightarrow {BP} \);
\(\overrightarrow {MN} \);
\(\overrightarrow {CP} \);
\(\overrightarrow {PA} \).
Cho \(\overrightarrow b \ne \overrightarrow 0 \) và điểm \(O\). Gọi \(M,\,N\) lần lượt là hai điểm thoả mãn \(\overrightarrow {OM} = 3\overrightarrow b ,\,\overrightarrow {ON} = - 4\overrightarrow b \) khi đó \(\overrightarrow {MN} \) bằng
\(7\overrightarrow b \);
\(5\overrightarrow b \);
\( - 7\overrightarrow b \);
\( - 5\overrightarrow b \).
Cho tam giác \(ABC\) đều có cạnh bằng \(2a\). Độ dài \(\overrightarrow {AB} + \overrightarrow {AC} \) bằng
\(2a\);
\(a\sqrt 3 \);
\(2a\sqrt 3 \);
\(\frac{{a\sqrt 3 }}{2}\).
Cho tam giác \[ABC\], gọi \[I\] là trung điểm của \[BC\]. Khẳng định nào sau đây đúng?
\[\overrightarrow {BI} = \overrightarrow {IC} \];
\[3\overrightarrow {BI} = 2\overrightarrow {IC} \];
\[\overrightarrow {BI} = 2\overrightarrow {IC} \];
\[2\overrightarrow {BI} = \overrightarrow {IC} \].
PHẦN 2II. PHẦN TỰ LUẬN (3 ĐIỂM)
(1,0 điểm) Một doanh nghiệp tư nhân A chuyên kinh doanh xe gắn máy các loại. Hiện nay doanh nghiệp đang tập trung chiến lược vào kinh doanh xe hon đa Future Fi với chi phí mua một chiếc là \(27\) triệu đồng và bán ra với giá là \(31\) triệu đồng. Với giá bán này thì số lượng xe mà khách hàng sẽ mua trong một năm là \(600\) chiếc. Nhằm mục tiêu đẩy mạnh hơn nữa lượng tiêu thụ dòng xe đang ăn khách này, doanh nghiệp dự định giảm giá bán và ước tính rằng nếu giảm \(1\) triệu đồng mỗi chiếc xe thì số lượng xe bán ra trong một năm sẽ tăng thêm \[200\] chiếc. Vậy doanh nghiệp phải bán với giá bao nhiêu sau khi giảm giá để lợi nhuận thu được là cao nhất.
(1,0 điểm)
a) Cho hai tập hợp \(M = \left( { - \infty ;2} \right)\) và \(N = \left[ { - 3;5} \right)\). Tìm \(M \cap N\).
b) Cho tam giác \[ABC\] vuông tại \[A\]. Điểm \[M\] bất kỳ nằm trong tam giác có hình chiếu xuống \[BC,\,AC,\,AB\] theo thứ tự là \[D,\,E,\,F\]. Tìm tập hợp điểm \[M\] biết rằng \[\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} \] cùng phương với \[\overrightarrow {BC} \].
(1,0 điểm)
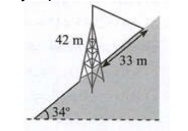
Một tháp viễn thông cao \(42\,\,m\) được dựng thẳng đứng trên một sườn dốc \(34^\circ \) so với phương ngang. Từ đỉnh tháp người ta neo một sợi cáp xuống một điểm trên sườn dốc cách chân tháp \(33\,\,m\) (như hình vẽ). Tính chiều dài của sợi dây cáp đó.