Bộ 10 đề thi Giữa kì 1 Toán 10 Cánh Diều có đáp án - Đề 10
76 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (7,0 điểm)
Nếu một cung tròn có số đo là \[a^\circ \] thì số đo radian của nó là
\[180\pi a.\]
\[\frac{{180\pi }}{a}.\]
\[\frac{{a\pi }}{{180}}.\]
\[\frac{\pi }{{180a}}.\]
Cho góc lượng giác \(\alpha = \left( {OA,OB} \right)\) có số đo bằng \(\frac{\pi }{5}\). Hỏi trong các số sau, số nào là số đo của một góc lượng giác có cùng tia đầu và tia cuối của góc \(\alpha ?\)
\(\frac{{6\pi }}{5}.\)
\( - \frac{{11\pi }}{5}.\)
\(\frac{{9\pi }}{5}.\)
\(\frac{{31\pi }}{5}.\)
Giá trị của \(\tan 180^\circ \) bằng
1.
0.
\( - 1.\)
Không xác định.
Khẳng định nào sai trong các khẳng định sau?
\(\cos 6a = {\cos ^2}3a - {\sin ^2}3a.\)
\(\cos 6a = 1 - 2{\sin ^2}3a.\)
\(\cos 6a = 1 - 6{\sin ^2}a.\)
\[\cos 6a = 2{\cos ^2}3a - 1.\]
Cho \(0 < \alpha < \frac{\pi }{2}.\) Khẳng định nào sau đây đúng?
\(\sin \left( {\alpha - \pi } \right) \ge 0.\)
\(\sin \left( {\alpha - \pi } \right) \le 0.\)
\(\sin \left( {\alpha - \pi } \right) < 0.\)
\(\sin \left( {\alpha - \pi } \right) < 0.\)
Rút gọn \(M = \cos \left( {a + b} \right)\cos \left( {a - b} \right) - \sin \left( {a + b} \right)\sin \left( {a - b} \right)\) ta được
\(M = 1 - 2{\cos ^2}a.\)
\(M = 1 - 2{\sin ^2}a.\)
\(M = \cos 4a.\)
\(M = \sin 4a.\)
Cho \(x,y\) là các góc nhọn, \(\cot x = \frac{4}{3}\) và \(\cot y = 7.\) Tổng \(x + y\) bằng
\(\frac{\pi }{3}.\)
\(\frac{\pi }{4}.\)
\(\frac{\pi }{6}.\)
\(\frac{{2\pi }}{3}.\)
Cho góc \[\alpha \] thỏa mãn \[\frac{\pi }{2} < \alpha < \pi \] và \[\sin \alpha = \frac{4}{5}\]. Giá trị của biểu thức \[P = \sin 2\left( {\alpha + \pi } \right)\] là
\(P = - \frac{{24}}{{25}}.\)
\(P = \frac{{24}}{{25}}.\)
\(P = - \frac{{12}}{{25}}.\)
\(P = \frac{{12}}{{25}}.\)
Khẳng định nào sau đây là sai về hàm số \(y = \cot x?\)
Hàm số \(y = \cot x\) có tập xác định là \[\mathbb{R}\backslash \left\{ {k\pi |k \in \mathbb{Z}} \right\}.\]
Hàm số \(y = \cot x\) có tập giá trị là \[\mathbb{R}.\]
Hàm số \(y = \cot x\) có đồ thị đối xứng qua trục tung.
Hàm số \(y = \cot x\) tuần hoàn với chu kì \(\pi .\)
Khẳng định nào sau đây là đúng?
Hàm số \(y = \tan x\) đồng biến trên khoảng \[\left( {0;\frac{\pi }{2}} \right).\]
Hàm số \(y = \cot x\) nghịch biến trên khoảng \(\left( {\frac{{3\pi }}{2};\frac{{5\pi }}{2}} \right).\)
Hàm số \(y = \sin x\) đồng biến trên khoảng \(\left( {0;\pi } \right).\)
Hàm số \(y = \cos x\) nghịch biến trên khoảng \(\left( {\frac{{3\pi }}{2};\frac{{5\pi }}{2}} \right).\)
Cho các khẳng định sau:
(1) Hàm số \(y = f\left( x \right)\) có tập xác định \(D\) được gọi là tuần hoàn nếu tồn tại một số \(T\) khác \(0\) sao cho với mọi \(x \in D\) ta có \(f\left( {x + T} \right) = f\left( x \right).\)
(2) Hàm số \(y = f\left( x \right)\) có tập xác định \(D\) được gọi là hàm số chẵn nếu \(\forall x \in D\) thì \( - x \in D\) và \(f\left( { - x} \right) = - f\left( x \right)\).
(3) Hàm số \(y = f\left( x \right)\) có tập xác định \(D\) được gọi là hàm số lẻ nếu \(\forall x \in D\) thì \( - x \in D\) và \(f\left( { - x} \right) = f\left( x \right).\)
Có bao nhiêu khẳng định sai trong các khẳng định trên?
0.
1.
2.
3.
Đồ thị hàm số \[y = \sin x\] được suy từ đồ thị \(\left( C \right)\) của hàm số \[y = \cos x\] bằng cách:
Dịch chuyển \(\left( C \right)\) qua trái một đoạn có độ dài là \[\frac{\pi }{2}.\]
Dịch chuyển \(\left( C \right)\) qua phải một đoạn có độ dài là \[\frac{\pi }{2}.\]
Dịch chuyển \(\left( C \right)\) lên trên một đoạn có độ dài là \[\frac{\pi }{2}.\]
Dịch chuyển \(\left( C \right)\) xuống dưới một đoạn có độ dài là \[\frac{\pi }{2}.\]
Giá trị nhỏ nhất \(m\) của hàm số \(y = \frac{1}{{\cos x + 1}}\) là
\[m = \frac{1}{2}.\]
\[m = \frac{1}{{\sqrt 2 }}.\]
\[m = 1.\]
\[m = \sqrt 2 .\]
Hàm số \(y = \sin \left( {x + \frac{\pi }{3}} \right) - \sin x\) có tất cả bao nhiêu giá trị nguyên?
1.
2.
3.
4.
Nghiệm của phương trình \(2\sin x = 1\) có tập nghiệm là
\(S = \left\{ {\frac{\pi }{6} + k2\pi ;\,\,\frac{{5\pi }}{6} + k2\pi ,k \in \mathbb{Z}} \right\}.\)
\(S = \left\{ {\frac{\pi }{3} + k2\pi ;\,\, - \frac{{2\pi }}{3} + k2\pi ,k \in \mathbb{Z}} \right\}.\)
\(S = \left\{ {\frac{\pi }{6} + k2\pi ;\,\, - \frac{\pi }{6} + k2\pi ,k \in \mathbb{Z}} \right\}.\)
\(S = \left\{ {\frac{\pi }{6} + k2\pi ,k \in \mathbb{Z}} \right\}.\)
Số điểm biểu diễn nghiệm của phương trình \(\sin x = \frac{4}{3}\) trên đường tròn lượng giác là
0.
1.
2.
4.
Một phương trình tương đương với phương trình \(\cos 2x + \cos 4x = \sin x - \sin 5x\) là
\(\cos 3x = 0.\)
\(\cos 3x = 1.\)
\(\sin 3x = 1.\)
\(2\sin 3x = 1.\)
Cung lượng giác có điểm biểu diễn là \({M_1},{M_2}\) như hình vẽ là nghiệm của phương trình lượng giác nào sau đây?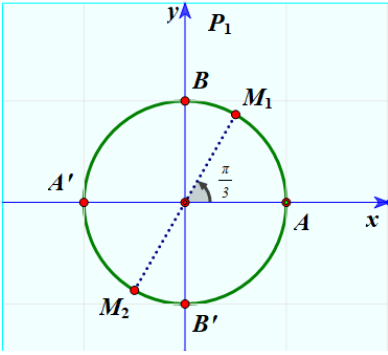
\(\sin \left( {x - \frac{\pi }{3}} \right) = 0.\)
\(\sin x = 0.\)
\(\cos \left( {x - \frac{\pi }{3}} \right) = 0.\)
\(\sin \left( {x + \frac{\pi }{3}} \right) = 0.\)
Nghiệm của phương trình \[{\cos ^2}x = 0\] là:
A. ![Nghiệm của phương trình \[{\cos ^2}x = 0\] là: (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/11/13-1762312266.png) .
.
B. ![Nghiệm của phương trình \[{\cos ^2}x = 0\] là: (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/11/14-1762312273.png) .
.
C. ![Nghiệm của phương trình \[{\cos ^2}x = 0\] là: (ảnh 3)](https://video.vietjack.com/upload2/quiz_source1/2025/11/15-1762312280.png) .
.
D. ![Nghiệm của phương trình \[{\cos ^2}x = 0\] là: (ảnh 4)](https://video.vietjack.com/upload2/quiz_source1/2025/11/16-1762312286.png) .
.
Phương trình lượng giác \(\sqrt 3 \tan \,x - 3 = 0\) có nghiệm là
\[x = \frac{\pi }{3} + k\pi \].
\[x = - \frac{\pi }{3} + k2\pi \].
\[x = \frac{\pi }{6} + k\pi \].
\[x = - \frac{\pi }{3} + k\pi \].
Cho dãy số \(\left( {{u_n}} \right)\), biết \({u_n} = \frac{n}{{{3^n} - 1}}\). Ba số hạng đầu tiên của dãy số đó lần lượt là những số nào dưới đây?
\(\frac{1}{2};\frac{1}{4};\frac{1}{8}.\)
\(\frac{1}{2};\frac{1}{4};\frac{3}{{26}}.\)
\(\frac{1}{2};\frac{1}{4};\frac{1}{{16}}.\)
\(\frac{1}{2};\frac{2}{3};\frac{3}{4}.\)
Cho dãy số \(\left( {{u_n}} \right),\) với \({u_n} = {5^{n + 1}}.\) Số hạng \({u_{n - 1}}\) là
\({u_{n - 1}} = {5^{n - 1}}.\)
\({u_{n - 1}} = {5^n}.\)
\({u_{n - 1}} = {5.5^{n + 1}}.\)
\({u_{n - 1}} = {5.5^{n - 1}}.\)
Cho dãy số \[\left( {{u_n}} \right),\] được xác định \[\left\{ \begin{array}{l}{u_1} = - 2\\{u_{n + 1}} = - 2 - \frac{1}{{{u_n}}}\end{array} \right..\] Số hạng tổng quát \[{u_n}\] của dãy số là số hạng nào dưới đây?
\[{u_n} = \frac{{ - n + 1}}{n}.\]
\[{u_n} = \frac{{n + 1}}{n}.\]
\[{u_n} = - \frac{{n + 1}}{n}.\]
\[{u_n} = - \frac{n}{{n + 1}}.\]
Trong các dãy số \[\left( {{u_n}} \right)\]cho bởi số hạng tổng quát \[{u_n}\] sau, dãy số nào là dãy số giảm?
\[{u_n} = \frac{1}{{{2^n}}}.\]
\[{u_n} = \frac{{3n - 1}}{{n + 1}}.\]
\[{u_n} = {n^2}.\]
\[{u_n} = \sqrt {n + 2} .\]
Trong các dãy số \(\left( {{u_n}} \right)\) sau đây, dãy số nào là dãy số bị chặn?
\({u_n} = \sqrt {{n^2} + 1} .\)
\({u_n} = n + \frac{1}{n}\,.\)
\({u_n} = {2^n} + 1.\)
\({u_n} = \frac{n}{{n + 1}}.\)
Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?
Ba điểm phân biệt\[.\]
Một điểm và một đường thẳng\[.\]
Hai đường thẳng cắt nhau\[.\]
Bốn điểm phân biệt\[.\]
Trong mặt phẳng \(\left( \alpha \right)\), cho 4 điểm \(A,\;B,\;C,\;D\) trong đó không có 3 điểm nào thẳng hàng. Điểm \(S\) không thuộc mặt phẳng \(\left( \alpha \right)\). Có mấy mặt phẳng tạo bởi \(S\) và 2 trong 4 điểm nói trên?
4.
5.
6.
8.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(I,{\rm{ }}J\) lần lượt là trung điểm \(SA,{\rm{ }}SB.\) Khẳng định nào sau đây sai?
\(IJCD\) là hình thang.
\(\left( {SAB} \right) \cap \left( {IBC} \right) = IB.\)
\(\left( {SBD} \right) \cap \left( {JCD} \right) = JD.\)
\(\left( {IAC} \right) \cap \left( {JBD} \right) = AO{\rm{ }}(O\) là tâm \(ABCD).\)
Cho tứ giác \(ABCD\) có \(AC\) và \(BD\) giao nhau tại \(O\) và một điểm \(S\) không thuộc mặt phẳng \(\left( {ABCD} \right)\). Trên đoạn \(SC\) lấy một điểm \(M\) không trùng với \(S\) và \(C.\) Giao điểm của đường thẳng \(SD\) với mặt phẳng \(\left( {ABM} \right)\) là
giao điểm của \(SD\) và \(AB.\)
giao điểm của \(SD\) và \(AM\).
giao điểm của \(SD\) và \(BK\) (với \(K = SO \cap AM\)).
giao điểm của \(SD\) và \(MK\) (với \(K = SO \cap AM\)).
Trong không gian, cho 3 đường thẳng \(a,\;b,\;c\), biết \(a\,{\rm{//}}\,b,\)\(a\) và \(c\) chéo nhau. Khi đó hai đường thẳng \(b\) và \(c\):
Trùng nhau hoặc chéo nhau.
Cắt nhau hoặc chéo nhau.
Chéo nhau hoặc song song.
Song song hoặc trùng nhau.
Trong không gian, cho 3 đường thẳng \(a,\;b,\;c\) chéo nhau từng đôi. Có nhiều nhất bao nhiêu đường thẳng cắt cả 3 đường thẳng ấy?
1.
2.
0.
Vô số.
Cho hình chóp\(S.ABCD\) có đáy là hình thang với các cạnh đáy là \(AB\) và \(CD.\) Gọi \(\left( {ACI} \right)\) lần lượt là trung điểm của \(AD\) và \(BC\) và \(G\) là trọng tâm của tam giác \(SAB.\) Giao tuyến của \(\left( {SAB} \right)\) và \(\left( {IJG} \right)\) là
\(SC.\)
đường thẳng qua \(S\) và song song với \(AB.\)
đường thẳng qua \(G\) và song song với \(DC.\)
đường thẳng qua \(G\) và cắt \(BC.\)
Cho tứ diện \[ABCD\] trong đó có tam giác \[BCD\] không cân. Gọi \[M,\,\,N\] lần lượt là trung điểm của \[AB,\,\,CD\] và \[G\] là trung điểm của đoạn \[MN.\] Gọi \[{A_1}\] là giao điểm của \[AG\] và \[\left( {BCD} \right).\] Khẳng định nào sau đây đúng?
\[{A_1}\] là tâm đường tròn tam giác \[BCD\,.\]
\({A_1}\) là tâm đường tròn nội tiếp tam giác \[BCD\,.\]
\({A_1}\) là trực tâm tam giác \[BCD\,.\]
\({A_1}\)là trọng tâm tam giác \[BCD\,.\]
Cho đường thẳng \(a\) nằm trong mặt phẳng \(\left( \alpha \right)\). Giả sử \[b \not\subset \left( \alpha \right)\]. Mệnh đề nào sau đây đúng?
Nếu \(b\,\,{\rm{//}}\,\left( \alpha \right)\) thì \[b\,\,{\rm{//}}\,\,a.\]
Nếu \(b\) cắt \(\left( \alpha \right)\) thì \(b\) cắt \(a.\)
Nếu \[b\,{\rm{//}}\,\,a\] thì \(b\,\parallel \,\left( \alpha \right).\)
Nếu \(b\) cắt \(\left( \alpha \right)\) và \(\left( \beta \right)\) chứa \[b\] thì giao tuyến của \(\left( \alpha \right)\) và \(\left( \beta \right)\) là đường thẳng cắt cả \(a\) và \(b.\)
Cho hình chóp tứ giác đều \[S.ABCD\] có cạnh đáy bằng \[10.\] \[M\] là điểm trên \[SA\] sao cho \[\frac{{SM}}{{SA}} = \frac{2}{3}.\] Một mặt phẳng \[\left( \alpha \right)\] đi qua \[M\] song song với \[AB\] và \[CD,\] cắt hình chóp theo một tứ giác có diện tích là
\(\frac{{400}}{9}.\)
\(\frac{{20}}{3}.\)
\(\frac{4}{9}.\)
\(\frac{{16}}{9}.\)
PHẦN II. TỰ LUẬN (3,0 điểm)
(1,5 điểm)
a) Cho góc \[\alpha \] thỏa mãn \[\frac{\pi }{2} < \alpha < \pi \] và \[\sin \alpha = \frac{4}{5}\]. Tính \[P = \sin 2\left( {\alpha + \pi } \right).\]
b) Tính tổng các nghiệm trên khoảng \(\left( { - \pi ;0} \right)\) của phương trình:
\(\sin 2x + \sqrt 2 \cos x = 0\).
c) Giả sử một vật dao động điều hoà xung quanh vị trí cân bằng theo phương trình
\(x = 2{\rm{cos}}\left( {5t - \frac{\pi }{6}} \right)\)
Ở đây, thời gian \(t\) tính bằng giây và quãng đường \(x\) tính bằng centimét. Hãy cho biết trong khoảng thời gian từ 0 đến 6 giây, vật đi qua vị trí cân bằng bao nhiêu lần?
(0,5 điểm) Xét tính tăng giảm của dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{\sqrt {n + 1} - 1}}{n}.\)
(1,0 điểm) Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông tâm \(O\), cạnh \(a\); tam giác \(SBD\) cân tại \(S\). Gọi \(M\) là điểm tùy ý trên \(AO\). Đặt \(AM = x\). Mặt phẳng \(\left( \alpha \right)\) qua \(M\) và song song với \(SA\), \(BD\) cắt \(SO,{\rm{ }}SB,{\rm{ }}AB\) tại \(N,{\rm{ }}P,{\rm{ }}Q\).
a) Tứ giác \(MNPQ\) là hình gì ?
b) Giả sử \(SA = a\). Tính diện tích tứ giác \(MNPQ\) theo \[a\] và \[x\]. Tìm \(x\) để diện tích \(MNPQ\) đạt giá trị lớn nhất.
I. PHẦN TRẮC NGHIỆM (7 ĐIỂM)
Mệnh đề kéo theo \(P \Rightarrow Q\) sai khi
\(P\) sai và \(Q\) đúng;
\(P\) sai và \(Q\) sai;
\(P\) đúng và \(Q\) sai;
\(P\) đúng và \(Q\) đúng.
Viết mệnh đề sau bằng cách sử dụng kí hiệu \(\forall \) hoặc \(\exists \): “Cho hai số thực khác nhau bất kì luôn tồn tại một số hữu tỉ nằm giữa hai số thực đã cho”.
\(\forall a,b \in \mathbb{R},a < b,\exists r \in \mathbb{Q}:a < r < b\);
\(\forall a,b \in \mathbb{R},\forall r \in \mathbb{Q}:a < r < b\);
\(\forall a,b \in \mathbb{R},a < b,\forall r \in \mathbb{Q}:a < r < b\)
\(\exists a,b \in \mathbb{R},\exists r \in \mathbb{Q}:a < r < b\).
Mệnh đề nào sau đây là mệnh đề phủ định của mệnh đề: “Mọi học sinh của lớp 10A đều thích học môn Toán”?
“Tất cả các bạn học sinh trong lớp 10A đều không thích môn Toán”;
“Có một học sinh của lớp 10A thích học môn Toán”;
“Có một học sinh trong lớp 10A không thích học môn Toán”;
“Mọi học sinh trong lớp 10A đều không thích học môn Toán”.
Cho tập hợp \(A = \left\{ {x \in {\mathbb{N}^*}|{x^3} - 8{x^2} + 15x = 0} \right\}\). Số phần tử của tập \(A\) là
\(2\);
\(3\);
\(0\);
\(1\).
Mệnh đề nào dưới đây là đúng?
\(\left( {0;\,\,3} \right] \subset \left( { - 1;\,3} \right)\);
\(\left( { - 1;2} \right) \subset \mathbb{Q}\);
\(\left( { - 1;\,\,4} \right) \cup \left[ {5;\,\,6} \right] \subset \mathbb{Z}\);
\(\left\{ {\frac{1}{2}} \right\} \subset \mathbb{Q}\).
Cho \(A,\,\,B,\,\,C\) là ba tập hợp bất kì khác rỗng, được biểu diễn bằng biểu đồ Ven như hình bên. Phần gạch sọc trong hình vẽ biểu diễn tập hợp nào sau đây?
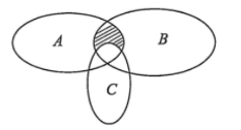
Phần gạch chéo trong hình tương ứng với tập hợp nào sau đây?
\(\left( {A \cup B} \right)\backslash C\);
\(\left( {A \cap B} \right)\backslash C\);
\(\left( {A \cap B} \right) \cap C\);
\(\left( {A \cap B} \right) \cup C\).
Lớp \(10A\) có \(26\)em thích bóng đá, \(30\) em thích bóng chuyền, \(15\) em thích cả bóng đá và bóng chuyền. Hỏi lớp \(10A\) có bao nhiêu học sinh (biết các học sinh của lớp đều thích ít nhất một trong hai môn trên)?
\(56\);
\(71\);
\(41\);
\(45\).
Gọi \(M\) là giá trị lớn nhất và \(m\) là giá trị nhỏ nhất của biểu thức \(F\left( {x;\,y} \right) = 4x - 3y\) trên miền nghiệm của hệ bất phương trình: \(\left\{ \begin{array}{l}x + y \ge 3\\x - y \le 5\\y \le 5\end{array} \right.\) được biểu diễn bởi hình vẽ sau:
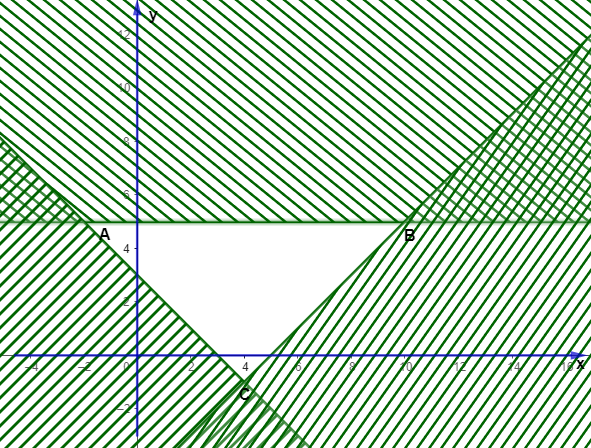
Giá trị \(M - m\) bằng
\(2\);
\(4\);
\(48\);
\(25\).
Bất phương trình nào là bất phương trình bậc nhất hai ẩn?
\(x - {12^2}y > 7\);
\(3x + 4{y^2} \le 7\);
\(\frac{2}{x} - 7y > 90\)
\(xy \ge - 9\).
Trong các hình dưới đây, hình nào biểu diễn miền nghiệm của bất phương trình \(\frac{1}{2}x - 3y \ge - 3\)?
A. 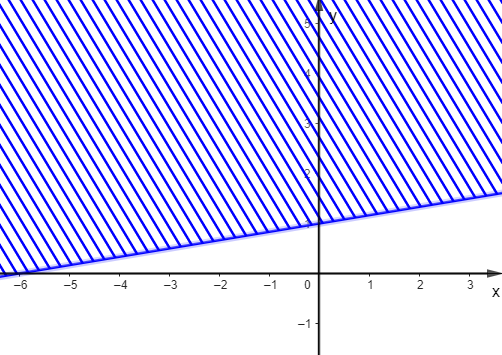 ;
;
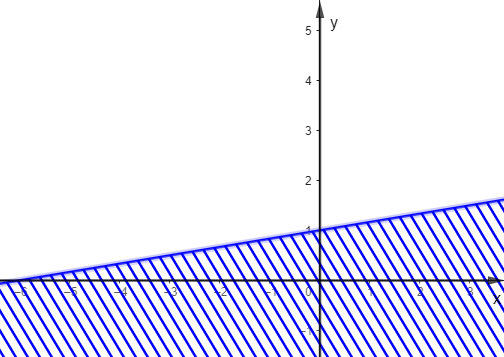
C. 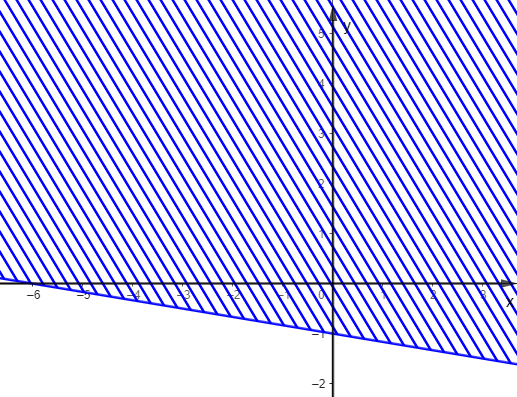 ;
;
D. 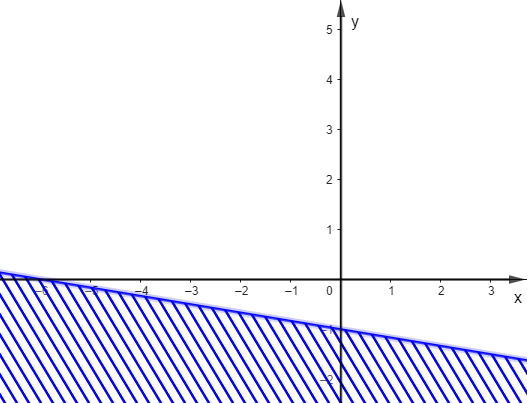 .
.
Cho bất phương trình bậc nhất hai ẩn: \(3mx - y < m + 1\). Với giá trị nào của tham số \(m\) thỏa mãn cặp \(\left( {0;\,\, - 2} \right)\) là nghiệm của bất phương trình đã cho?
\(m = \frac{5}{4}\);
\(m = - \frac{1}{2}\);
\(m = 2\frac{1}{4}\);
\(m = 1\).
Cho hệ bất phương trình \(\left\{ \begin{array}{l}x + y < 0\\y \ge 0\\x \ge - 1\end{array} \right.\). Điểm \(M\left( {{x_0};\,\,{y_0}} \right)\) là điểm thỏa mãn miền nghiệm của hệ bất phương trình trên. Khi đó biểu thức nào dưới đây là đúng?
\({x_0} + {y_0} \ge 0\);
\({x_0} < 0\);
\({y_0} \ge - 1\);
\({x_0} - {y_0} > - 1\).
Cho hệ bất phương trình \(\left\{ \begin{array}{l}x - y < 1\\x + 2y \ge 0\end{array} \right.\) có miền nghiệm được biểu diễn như hình vẽ:
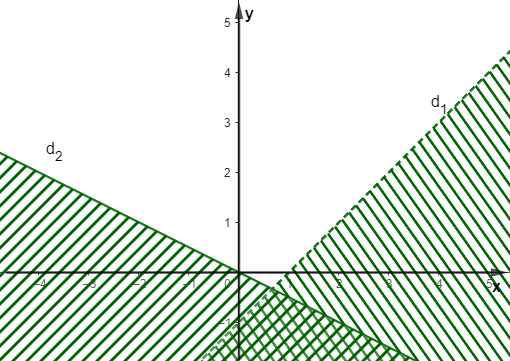
Câu nào mô tả đúng nhất miền nghiệm của hệ bất phương trình trên?
Miền nghiệm của hệ bất phương trình là miền bị gạch chéo trong hình vẽ kể cả hai đường thẳng \({d_1}\) và \({d_2}\);
Miền nghiệm của hệ bất phương trình là miền bị gạch chéo trong hình vẽ không kể cả hai đường thẳng \({d_1}\) và \({d_2}\);
Miền nghiệm của hệ bất phương trình là miền không bị gạch chéo trong hình vẽ kể đường thẳng \({d_1}\) và không kể đường thẳng \({d_2}\);
Miền nghiệm của hệ bất phương trình là miền không bị gạch chéo trong hình vẽ không kể đường thẳng \({d_1}\) và kể cả đường thẳng \({d_2}\).
Trong các cặp số: \(\left( {0;\,\,0} \right);\,\,\,\left( { - 1;\,\,1} \right);\,\,\left( { - 2;\,\,3} \right)\,;\,\,\left( {4;\,\,1} \right)\) có bao nhiêu cặp số là nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x - 2y \le 1\\2x - y > - 2\end{array} \right.\)?
\(1\);
\(2\);
\(3\);
\(4\).
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên:
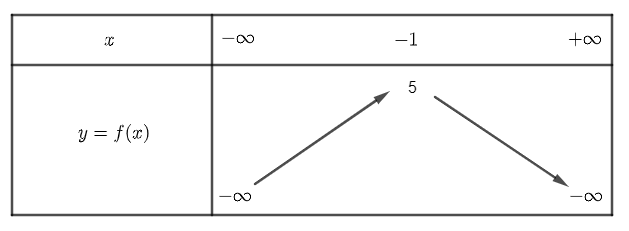
Nhận xét nào dưới đây là đúng?
Hàm số đồng biến trên khoảng \(\left( {1; + \infty } \right)\);
Hàm số đạt giá trị nhỏ nhất là âm vô cực;
Hàm số đạt giá trị lớn nhất là \( - 1\);
Hàm số nghịch biến trên khoảng \(\left( { - \infty ;1} \right)\).
Cho đồ thị hàm số sau:
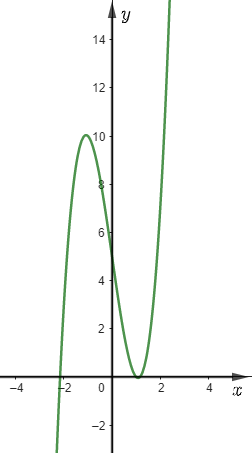
Gọi \(M\) là giá trị lớn nhất của hàm số. Khi đó
\(M = 10\);
\(M = 0\);
\(M = + \infty \);
\(M \in \emptyset \).
Hàm số nào dưới đây có tập xác định là \(\mathbb{R}\)?
\(y = \frac{{\sqrt {{x^2} + 2} }}{{2x}}\);
\(y = {x^3} - \frac{{\left| x \right|}}{2}\);
\(y = \sqrt {x - 9} \);
\(y = \frac{1}{{\left| x \right|}}\).
Toạ độ đỉnh của hàm số \(y = {x^2} + 2x - 1\) là \(I\left( {m;n} \right)\). Giá trị của \(m + n\) bằng:
\( - 1\);
\(1\);
\(3\);
\( - 3\).
Cho hàm số bậc hai \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\) có đồ thị như hình vẽ:
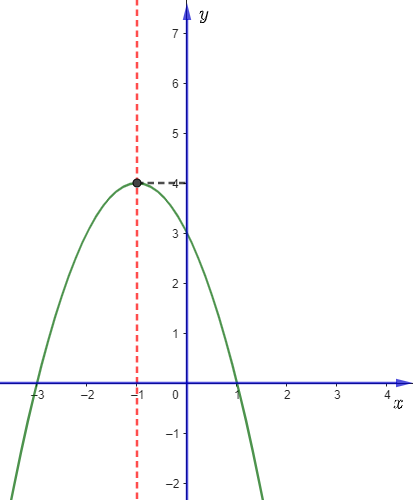
Kết luận nào dưới đây là đúng?
\(a > 0,\,\,b < 0,\,\,c > 0\);
\(a < 0,\,\,b > 0,\,\,c > 0\);
\(a < 0,\,\,b < 0,\,\,c > 0\);
\(a < 0,\,\,b > 0,\,\,c < 0\).
Trong các đẳng thức sau đây, đẳng thức nào sai?
\(\sin 0^\circ + {\rm{cos}}0^\circ = 1\);
\({\sin ^2}30^\circ + {\rm{co}}{{\rm{s}}^2}60^\circ = 1\);
\(\sin 90^\circ + {\rm{cos9}}0^\circ = 1\);
\({\sin ^2}120^\circ + {\rm{co}}{{\rm{s}}^2}120^\circ = 1\).
Cho góc \(90^\circ < \alpha < 180^\circ \). Biết rằng \(\sin \alpha = \frac{1}{3}\). Tính giá trị của \(\cos \alpha \).
\(\cos \alpha = \frac{2}{3}\).
\(\cos \alpha = - \frac{2}{3}\).
\(\cos \alpha = \frac{{2\sqrt 2 }}{3}\).
\(\cos \alpha = \frac{{ - 2\sqrt 2 }}{3}\).
Từ vị trí \(A\) cách mặt đất \(1m\), một bạn nhỏ quan sát một cây đèn đường (hình vẽ).
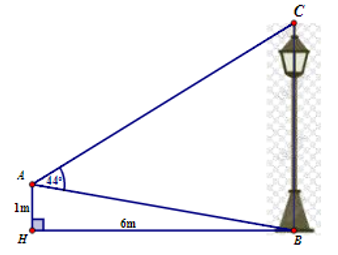
Biết \(HB = 6\,\,m\), \(\widehat {BAC} = 44^\circ \). Chiều cao của cây đèn đường gần nhất với giá trị nào sau đây?
\(5,1\,\,m\);
\(7,2\,m\);
\(5,9\,\,m\);
\(8,3\,\,m\).
Cho tam giác \(ABC\) thỏa mãn \({\sin ^2}A = \sin B.\sin C\). Khẳng định nào dưới đây là đúng?
\[{\rm{cos}}\frac{A}{2} \le \frac{1}{2}\];
\[{\rm{cos}}A \ge \frac{1}{2}\];
\[{\rm{cos}}A = 0\];
\[{\rm{cos}}A < \frac{1}{2}\].
Cho tam giác \(ABC\) có \[BC = a,\,AC = b,\,AB = c\] và \(R\) là bán kính đường tròn ngoại tiếp tam giác. Công thức nào sau đây sai?
\(\frac{a}{{\sin A}} = 2R\);
\(\sin A = \frac{a}{{2R}}\);
\(b\sin B = 2R\);
\(\sin C = \frac{{c\sin A}}{a}\).
Cho tam giác \(ABC\) có \(AB = 2\,\,cm\), \(\widehat {ABC} = 60^\circ \), \(\widehat {BAC} = 75^\circ \). Diện tích tam giác \(ABC\) gần nhất với giá trị nào sau đây?
\(2,37\,\,c{m^2}\);
\(0,63\,\,c{m^2}\);
\(2,45\,\,c{m^2}\);
\(1,58\,\,c{m^2}\).
Tam giác \(ABC\) vuông cân tại \(A\) nội tiếp trong đường tròn tâm \(O\) bán kính \(R\) và có bán kính đường tròn nội tiếp tam giác là \(r\). Khi đó tỉ số \(\frac{R}{r}\) là
\(1 + \sqrt 2 \);
\(\frac{{2 + \sqrt 2 }}{2}\);
\(\frac{{\sqrt 2 - 1}}{2}\);
\(\frac{{1 + \sqrt 2 }}{2}\).
Cho \(\alpha \) và \(\beta \) là hai góc khác nhau và bù nhau. Trong các đẳng thức sau đây, đẳng thức nào sai?
\(\sin \alpha = \sin \beta \);
\(\cos \alpha = - \cos \beta \);
\(\tan \alpha = - \tan \beta \);
\(\cot \alpha = \cot \beta \).
Chọn khẳng định đúng.
Hai vectơ cùng hướng thì có giá song song;
Hai vectơ cùng phương thì có giá song song;
Hai vectơ cùng hướng thì cùng phương;
Hai vectơ cùng phương thì cùng hướng.
Trong các đại lượng sau, đại lượng nào cần được biểu diễn bởi vectơ?
Diện tích;
Thể tích;
Giá tiền;
Lực.
Cho hình bình hành \(ABCD\). Khẳng định nào sau đây là sai?
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \);
\(\overrightarrow {DA} + \overrightarrow {DC} = \overrightarrow {DB} \);
\(\overrightarrow {AC} = \overrightarrow {BD} \);
\(\overrightarrow {AB} = \overrightarrow {DC} \).
Cho lục giác đều \(ABCDEF\) có tâm \(O\). Đẳng thức nào sau đây là đúng?
\(\overrightarrow {OA} + \overrightarrow {OB} - \overrightarrow {EO} = \overrightarrow 0 \);
\(\overrightarrow {BC} - \overrightarrow {FE} = \overrightarrow {AD} \);
\(\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {EB} - \overrightarrow {OC} \);
\(\overrightarrow {AB} + \overrightarrow {CD} - \overrightarrow {FE} = \overrightarrow 0 \).
Cho hình chữ nhật \(ABCD\) có \(AB = 3a,\,\,AD = a\). Khi đó, \(\left| {\overrightarrow {BA} + \overrightarrow {AC} + \overrightarrow {CD} } \right|\) bằng
\(a\sqrt {10} \);
\(4a\);
\(3a\);
\(5a\).
Cho vectơ \(\overrightarrow a \) khác \(\overrightarrow 0 \) và một số thực \(k \ne 0\). Khẳng định nào sau đây là đúng?
Hai vectơ \(\overrightarrow a ,\,\,k\overrightarrow a \) luôn cùng phương;
Hai vectơ \(\overrightarrow a ,\,\,k\overrightarrow a \) luôn cùng hướng;
Hai vectơ \(\overrightarrow a ,\,\,k\overrightarrow a \) có độ dài bằng nhau;
Hai vectơ \(\overrightarrow a ,\,\,k\overrightarrow a \) luôn ngược hướng.
Cho hình thang \(MNPQ\) có \(MN\,{\rm{//}}\,PQ,\,MN = 2PQ\). Phát biểu nào sau đây là đúng?
\(\overrightarrow {MN} = 2\overrightarrow {PQ} \);
\(\overrightarrow {MQ} = 2\overrightarrow {NP} \);
\(\overrightarrow {MN} = - 2\overrightarrow {PQ} \);
\(\overrightarrow {MQ} = - 2\overrightarrow {NP} \).
Đẳng thức nào sau đây mô tả đúng hình vẽ dưới?

\(\overrightarrow {MP} = \frac{1}{2}\overrightarrow {NP} \);
\(\overrightarrow {MP} = - \frac{1}{2}\overrightarrow {NP} \);
\(\overrightarrow {MN} = 6\overrightarrow {MP} \);
\(\overrightarrow {MN} = 3\overrightarrow {PM} \).
II. PHẦN TỰ LUẬN (3 ĐIỂM)
(1 điểm)
a) Xác định điều kiện của \(a,b\) để \(A \cap B = \emptyset \) với \(A = \left[ {a - 1;\,\,a + 2} \right]\) và \(B = \left( {b;\,\,b + 4} \right]\).
b) Cho tam giác \(ABC\) có \(G\) là trọng tâm. Gọi \(D\) và \(E\) lần lượt là các điểm thỏa mãn đẳng thức \(\overrightarrow {AD} = 2\overrightarrow {AB} ,\overrightarrow {AE} = x\overrightarrow {AC} \). Tìm \(x\) để ba điểm \(D,\,\,G,\,\,E\) thẳng hàng. Với giá trị tìm được của \(x\), hãy tính tỉ số \(\frac{{DG}}{{DE}}\).
(1,0 điểm) Anh An làm nghề thợ mộc chuyên đóng bàn và ghế học sinh. Mỗi cái bàn anh bán lãi được \(150\) nghìn đồng, mỗi cái ghế bán lãi được \(100\) nghìn đồng. Mỗi tuần anh làm việc không quá \(60\) giờ. Anh đóng một cái bàn tốn hết \(6\) giờ và đóng một cái ghế tốn hết \(3\) giờ. Để có lãi, anh An phải làm số ghế nhiều hơn số bàn ít nhất \(2\) lần. Hỏi một tuần anh An phải đóng bao nhiêu cái bàn, bao nhiêu cái ghế để số tiền lãi thu về lớn nhất?
(1,0 điểm) Cho các địa điểm \(A,B\) và \(C\) (như hình vẽ) biết \(AB = 100\,\,km,\,AC = 150\,\,km,\widehat {ABC} = 110^\circ \). Bạn An muốn đi từ \(A\) đến \(C\) bằng một trong hai cách sau đây:
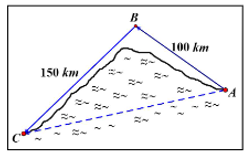
Cách 1: Đi tàu thủy từ \(A\) và \(C\) với vận tốc \(30\,\,km/h\).
Cách 2: Đi xe hơi từ \(A\) và \(B\) rồi từ \(B\) đến \(C\) với vận tốc \(50\,\,km/h\).
Hỏi đi cách nào thì An sẽ đến \(C\) sớm hơn?








