Quiz

Đề thi Giữa kì 1 Toán 10 chân trời sáng tạo có đáp án - Đề 1

VietJackToánLớp 107 lượt thi

Bắt đầu ngay

31 câu hỏi

Hiển thị đáp án

1. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho các câu sau đây:

a) Không được nói chuyện!

b) Ngày mai bạn đi học không?

c) Chủ tịch Hồ Chí Minh sinh năm 1890.

d) 22 chia 3 dư 1.

e) 2005 không là số nguyên tố.

Có bao nhiêu câu là mệnh đề ?

Xem đáp án

2. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hai mệnh đề P: “x là số chẵn” và Q: “x chia hết cho 2”.

Phát biểu mệnh đề P kéo theo Q.

Hoặc x là số chẵn hoặc x chia hết cho 2;

Nếu x là số chẵn thì x chia hết cho 2;

Nếu x chia hết cho 2 thì x là số chẵn;

x là số chẵn và x chia hết cho 2.

Xem đáp án

3. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho tập hợp A là các nghiệm của phương trình x² – 6x + 5 = 0.

Viết tập hợp trên dưới dạng liệt kê các phần tử.

A = {2 ; 3};

A = {1 ; 5};

A = {4 ; 6};

A = {2 ; 4}.

Xem đáp án

4. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho tập hợp H = [1; 7] ∩ (– 3; 5). Đáp án nào sau đây là đúng.

H = [1; 7];

H = (– 3; 5);

H = [1; 5] ;

H = [1; 5).

Xem đáp án

5. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hai tập hợp A = (0; 3), B = (2; 4). Xác định A \ B.

A \ B = (0; 2];

A \ B = (0; 2);

A \ B = (0; 4);

A \ B = [3; 4).

Xem đáp án

6. Trắc nghiệm

• 1 điểm • Không giới hạn

Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn ?

2x – 4y + 7 ≥ 0;

5x³ – 4y³ – 2 ≤ 0;

x³ – 2y < 0;

x² + 3 > 0.

Xem đáp án

7. Trắc nghiệm

• 1 điểm • Không giới hạn

Cặp số (–1; 3) là một nghiệm của bất phương trình:

–3x + 2y – 4 > 0;

x + 3y < 0;

3x – y > 0;

2x – y + 4 > 0.

Xem đáp án

8. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong các hệ bất phương trình sau, đâu không là hệ bất phương trình bậc nhất hai ẩn:

$\{\begin{cases} x + y \geq 10 \\ x - 3 y < 6 \end{cases}$

$\{\begin{cases} 2 x - y - 1 > 0 \\ x - 2 > 0 \\ x + 5 y < 4 \end{cases}$

$\{\begin{cases} 3 x + 2 y - 2 < 0 \\ 3 x - y < 4 - y \\ 5 + x^{2} < 3 \end{cases}$

$\{\begin{cases} 7 x - y < 1 \\ x + 2 y < 3 y - x \end{cases}$

Xem đáp án

9. Trắc nghiệm

• 1 điểm • Không giới hạn

Trong các đẳng thức sau đây, đẳng thức nào đúng?

sin60° = $\frac{\sqrt{3}}{2}$ ;

cos60° = $\frac{\sqrt{3}}{2}$ ;

tan60° = 1;

cot60° = −1.

Xem đáp án

10. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho α là góc nhọn. Khẳng định nào sau đây là đúng?

sin α < 0;

cos α < 0;

tan α < 0;

cot α > 0.

Xem đáp án

11. Trắc nghiệm

• 1 điểm • Không giới hạn

Chọn đáp án sai: Một tam giác giải được nếu biết:

Độ dài 3 cạnh;

Độ dài 2 cạnh và 1 góc bất kỳ;

Số đo 3 góc;

Độ dài 1 cạnh và 2 góc bất kỳ.

Xem đáp án

12. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình vuông ABCD tâm O. Giá của vectơ $\underset{A O}{\to}$ là:

Đường thẳng AC;

Đường thẳng BC;

Đường thẳng AB;

Đường thẳng DO.

Xem đáp án

13. Trắc nghiệm

• 1 điểm • Không giới hạn

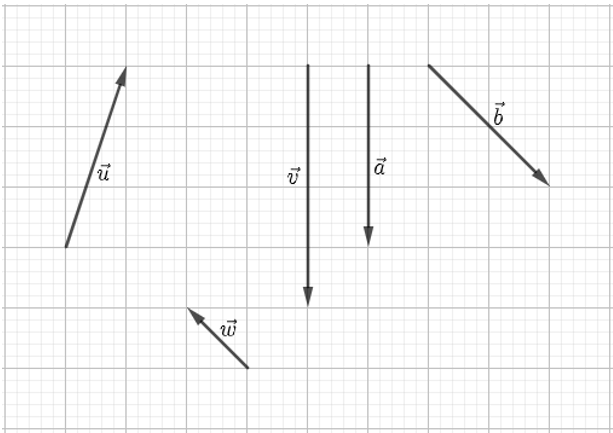
Cho hình vẽ dưới đây. Khẳng định nào sau đây là đúng ? (ảnh 1)

Khẳng định nào sau đây là đúng ?

Trong hình có 3 cặp vectơ cùng phương;

$\underset{u}{\to}$ và $\underset{w}{\to}$ cùng phương;

$\underset{u}{\to}$ và $\underset{b}{\to}$ cùng phương;

$\underset{a}{\to}$ và $\underset{v}{\to}$ cùng phương.

Xem đáp án

14. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho 4 điểm A, B, C, D. Ta có: $\underset{A B}{\to} + \underset{B D}{\to} = ?$

$\underset{A C}{\to} + \underset{B D}{\to}$

$\underset{AD}{\to} + \underset{D B}{\to}$

$\underset{A C}{\to} + \underset{C D}{\to}$

$\underset{D A}{\to} + \underset{D B}{\to}$

Xem đáp án

15. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình vuông ABCD tâm O. Khi đó, $\underset{O A}{\to} - \underset{O B}{\to} = ?$

$\underset{C D}{\to}$ .

$\underset{A B}{\to}$

$\underset{A C}{\to}$

$\underset{B D}{\to}$

Xem đáp án

16. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho tam giác đều ABC cạnh 4. Vectơ $- \frac{1}{2} \underset{B C}{\to}$ có độ dài là.

Xem đáp án

17. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho tam giác ABC có a = 4, b = 6 và cosC = $\frac{2}{3}$ . Giá trị của c bằng

$3 \sqrt{5}$

$2 \sqrt{5}$

$5 \sqrt{2}$

$5 \sqrt{3}$

Xem đáp án

18. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho $\underset{a}{\to}$ và $\underset{b}{\to}$ không cùng phương và hai vectơ $\underset{x}{\to} = \underset{2 a}{\to} + \underset{b}{\to}$ và $\underset{y}{\to} = - 4 \underset{a}{\to} - 2 \underset{b}{\to}$ . Khẳng định nào sau đây là đúng ?

$\underset{x}{\to}$ và $\underset{y}{\to}$ cùng phương, cùng hướng;

$\underset{x}{\to}$ và $\underset{y}{\to}$ không cùng phương;

$\underset{x}{\to}$ và $\underset{y}{\to}$ bằng nhau;

$\underset{x}{\to}$ và $\underset{y}{\to}$ cùng phương, ngược hướng.

Xem đáp án

19. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho tam giác ABC có $μ = 60 °$ , $γ = 45 °$ , b = 4. Tính cạnh a.

$2 \sqrt{6}$

$3 \sqrt{6}$

$6 \sqrt{2}$

$6 \sqrt{3}$

Xem đáp án

20. Trắc nghiệm

• 1 điểm • Không giới hạn

Phần tô đậm trong hình vẽ sau biểu diễn tập nghiệm của bất phương trình nào trong các bất phương trình sau?

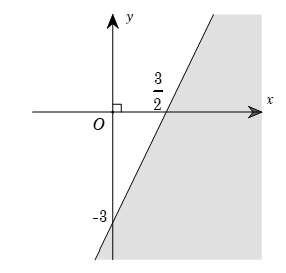
Phần tô đậm trong hình vẽ sau biểu diễn tập nghiệm của bất phương trình nào trong các bất phương trình sau? (ảnh 1)

2x – y < 3;

2x – y > 3;

x – 2y < 3;

x – 2y > 3.

Xem đáp án

21. Trắc nghiệm

• 1 điểm • Không giới hạn

Mệnh đề nào dưới đây có mệnh đề phủ định của nó là đúng?

“∀x ∈ ℝ: x < x + 2”;

“∀n ∈ ℕ: 3n ≥ n”;

“∃x ∈ ℚ: x² = 5”;

“∃x ∈ ℝ: x² – 3 = 2x”.

Xem đáp án

22. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình chữ nhật ABCD tâm O có: AD = a, AB = 2a. Tính $\underset{A B}{\to} . \underset{A O}{\to}$ =?

a²;

2a².

Xem đáp án

23. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho tam giác ABC vuông cân tại C và AB = $\sqrt{2}$ . Tính $|\begin{matrix} \underset{A B}{\to} - \underset{A C}{\to} \end{matrix}|$ .

Xem đáp án

24. Trắc nghiệm

• 1 điểm • Không giới hạn

Biết sin α + cos α = $\sqrt{2}$ . Giá trị của biểu thức Q = sin⁴α – cos⁴α là:

– 1;

Xem đáp án

25. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho A = (– ∞; – 2], B = [3; + ∞), C = (0; 4). Khi đó tập (A ∪ B) ∩ C là:

[3; 4];

(– ∞; – 2] ∪ (3; + ∞);

[3; 4);

(– ∞; – 2) ∪ [3; + ∞).

Xem đáp án

26. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hình bình hành ABCD và điểm M, biết $|\begin{matrix} \underset{B M}{\to} - \underset{B A}{\to} \end{matrix}| = |\begin{matrix} \underset{A B}{\to} + \underset{A D}{\to} \end{matrix}|$ . Điểm M là:

Điểm thuộc đường tròn tâm A, bán kính AC;

Điểm thuộc đường tròn tâm A, bán kính BD;

Điểm thuộc đường tròn tâm B, bán kính AC;

Điểm thuộc đường tròn tâm B, bán kính BD.

Xem đáp án

27. Trắc nghiệm

• 1 điểm • Không giới hạn

Tam giác DEF có DE = 5, DF = 8 và EDF=50 $°$ . Bán kính r của đường tròn nội tiếp tam giác đã cho gần nhất với giá trị nào sau đây?

1,5;

15;

20.

Xem đáp án

28. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho hai điểm A, B và O là trung điểm của AB. Gọi M là một điểm tùy ý, khẳng định nào sau đây là đúng ?

$\underset{M A}{\to} . \underset{M B}{\to} = O M^{2} - O A^{2}$

$\underset{M A}{\to} . \underset{M B}{\to} = O M^{2} + O A^{2}$

$\underset{M A}{\to} . \underset{M B}{\to} = O M^{2} - 2 O A^{2}$

$\underset{M A}{\to} . \underset{M B}{\to} = O M^{2} + 2 O A^{2}$

Xem đáp án

29. Trắc nghiệm

• 1 điểm • Không giới hạn

Cho tam giác ABC. Đặt $\underset{A B}{\to} = \underset{a}{\to}$ , $\underset{A C}{\to} = \underset{b}{\to}$ . M thuộc cạnh AB sao cho AB = 3AM, N thuộc tia BC và CN = 2BC. Phân tích $\underset{M N}{\to}$ qua các vectơ $\underset{a}{\to}$ và $\underset{b}{\to}$ ta được biểu thức là: