24 câu hỏi
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN
A. TRẮC NGHIỆM NHIỀU PHƯƠNG ÁN LỰA CHỌN. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Mệnh đề nào dưới đây là mệnh đề sai?
Tổng hai cạnh bất kì của một tam giác lớn hơn cạnh thứ ba.
Số \(21\) không phải là số lẻ.
Số \(12\) chia hết cho \(3\).
Số \(\pi \) không phải là số hữu tỉ.
Mệnh đề nào dưới đây là mệnh đề sai?
Tổng hai cạnh bất kì của một tam giác lớn hơn cạnh thứ ba.
Số \(21\) không phải là số lẻ.
Số \(12\) chia hết cho \(3\).
Số \(\pi \) không phải là số hữu tỉ.
Hình vẽ nào sau đây minh họa cho tập hợp \(\left( {1;4} \right]\)?
A. 
C. 
Hình vẽ nào sau đây minh họa cho tập hợp \(\left( {1;4} \right]\)?
B.
D.
Tập hợp \(N = \left\{ {x \in \mathbb{N}|x < 5} \right\}\) có bao nhiêu phần tử?
\(n\left( N \right) = 4\).
\(n\left( N \right) = 0\).
\(n\left( N \right) = 5\).
\(n\left( N \right) = 6\).
Tập hợp \(N = \left\{ {x \in \mathbb{N}|x < 5} \right\}\) có bao nhiêu phần tử?
\(n\left( N \right) = 4\).
\(n\left( N \right) = 0\).
\(n\left( N \right) = 5\).
\(n\left( N \right) = 6\).
Bất phương trình nào sau đây không phải là là bất phương trình bậc nhất hai ẩn?
\[ - x + 4y > 7\].
\[2x - 4 + 3 \le 0\].
\[3x + 2 < 0\].
\[{x^2} - 3y \le 0\].
Bất phương trình nào sau đây không phải là là bất phương trình bậc nhất hai ẩn?
\[ - x + 4y > 7\].
\[2x - 4 + 3 \le 0\].
\[3x + 2 < 0\].
\[{x^2} - 3y \le 0\].
Trong các hệ bất phương trình dưới đây, hệ bất phương trình nào là hệ bất phương trình bậc nhất hai ẩn?
\(\left\{ \begin{array}{l}x + y + z > 10\\2x + y \le 12\end{array} \right.\).
\(\left\{ \begin{array}{l} - x + 2y \le 10\\2x + {y^2} > 0\end{array} \right.\).
\(\left\{ \begin{array}{l}x + y \le 10\\2x + y = 3\end{array} \right.\).
\(\left\{ \begin{array}{l}x + y \le 1\\2x + y > 10\end{array} \right.\).
Trong các hệ bất phương trình dưới đây, hệ bất phương trình nào là hệ bất phương trình bậc nhất hai ẩn?
\(\left\{ \begin{array}{l}x + y + z > 10\\2x + y \le 12\end{array} \right.\).
\(\left\{ \begin{array}{l} - x + 2y \le 10\\2x + {y^2} > 0\end{array} \right.\).
\(\left\{ \begin{array}{l}x + y \le 10\\2x + y = 3\end{array} \right.\).
\(\left\{ \begin{array}{l}x + y \le 1\\2x + y > 10\end{array} \right.\).
Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x > 0\\x + y \le 2\\x - y > 1\end{array} \right.\) chứa điểm nào sau đây?
\(B\left( {1\,;\,2} \right)\).
\(A\left( {1\,;\, - 1} \right)\).
\(C\left( {0\,;\,2} \right)\).
\[D\left( {3\,;\,1} \right)\]
Miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x > 0\\x + y \le 2\\x - y > 1\end{array} \right.\) chứa điểm nào sau đây?
\(B\left( {1\,;\,2} \right)\).
\(A\left( {1\,;\, - 1} \right)\).
\(C\left( {0\,;\,2} \right)\).
\[D\left( {3\,;\,1} \right)\].
Cho \(0^\circ < \alpha < 180^\circ \). Chọn khẳng định sai.
\(\sin \alpha = \sin \left( {180^\circ - \alpha } \right)\).
\[{\sin ^2}\alpha + {\cos ^2}\alpha = 1\].
\(\sin \alpha + \cos \alpha = 1\).
\(\cos \alpha + \cos \left( {180^\circ - \alpha } \right) = 0\).
Cho \(0^\circ < \alpha < 180^\circ \). Chọn khẳng định sai.
\(\sin \alpha = \sin \left( {180^\circ - \alpha } \right)\).
\[{\sin ^2}\alpha + {\cos ^2}\alpha = 1\].
\(\sin \alpha + \cos \alpha = 1\).
\(\cos \alpha + \cos \left( {180^\circ - \alpha } \right) = 0\).
Cho tam giác \(ABC\) có \(BC = a,\,\,AC = b,\,AB = c\). Gọi \(p\) là nửa chu vi, \(R\) là bán kính đường tròn ngoại tiếp, \(r\) là bán kính đường tròn nội tiếp và \(S\) là diện tích tam giác. Mệnh đề nào sau đây sai?
\(S = pr\).
\(S = \frac{1}{2}ab\sin C\).
\(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \).
\(S = \frac{{abc}}{{2{\rm{R}}}}\)
Cho tam giác \(ABC\) có \(BC = a,\,\,AC = b,\,AB = c\). Gọi \(p\) là nửa chu vi, \(R\) là bán kính đường tròn ngoại tiếp, \(r\) là bán kính đường tròn nội tiếp và \(S\) là diện tích tam giác. Mệnh đề nào sau đây sai?
\(S = pr\).
\(S = \frac{1}{2}ab\sin C\).
\(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \).
\(S = \frac{{abc}}{{2{\rm{R}}}}\).
Cho tam giác \(ABC\) có \(AB = 4\)cm, \(BC = 7\) cm, \(AC = 9\)cm. Tính \(\cos A
\(\cos A = \frac{1}{2}\).
\(\cos A = - \frac{2}{3}\).
\(\cos A = \frac{2}{3}\).
\(\cos A = \frac{1}{3}\).
Cho tam giác \(ABC\) có \(AB = 4\)cm, \(BC = 7\) cm, \(AC = 9\)cm. Tính \(\cos A\).
\(\cos A = \frac{1}{2}\).
\(\cos A = - \frac{2}{3}\).
\(\cos A = \frac{2}{3}\).
\(\cos A = \frac{1}{3}\).
Trong các mệnh đề sau, mệnh đề nào đúng?
“\(\exists n \in \mathbb{N},n\left( {n + 1} \right)\left( {n + 2} \right)\) là số lẻ”.
“\(\forall x \in \mathbb{R},{x^2} < 4 \Leftrightarrow - 2 < x < 2\)”.
“\(\exists n \in \mathbb{N},{n^2} + 1\) chia hết cho 3”.
“\(\forall x \in \mathbb{R},{x^2} \ge 9 \Leftrightarrow x \ge \pm 3\)”.
Trong các mệnh đề sau, mệnh đề nào đúng?
“\(\exists n \in \mathbb{N},n\left( {n + 1} \right)\left( {n + 2} \right)\) là số lẻ”.
“\(\forall x \in \mathbb{R},{x^2} < 4 \Leftrightarrow - 2 < x < 2\)”.
“\(\exists n \in \mathbb{N},{n^2} + 1\) chia hết cho 3”.
“\(\forall x \in \mathbb{R},{x^2} \ge 9 \Leftrightarrow x \ge \pm 3\)”.
Miền nghiệm của bất phương trình \(3x - 2y > - 6\) là phần không bị gạch trong hình vẽ nào sau đây?
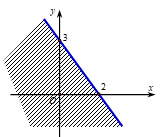
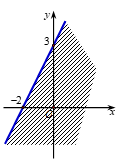
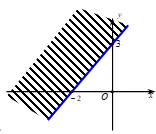
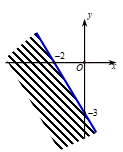
Miền nghiệm của bất phương trình \(3x - 2y > - 6\) là phần không bị gạch trong hình vẽ nào sau đây?
B.
D.
Giá trị của biểu thức \(A = \cos 10^\circ + \cos 20^\circ + ... + \cos 170^\circ + \cos 180^\circ \) bằng
\(A = \frac{3}{2}\).
\(A = 0\).
\(A = 1\).
\(A = - 1\).
Giá trị của biểu thức \(A = \cos 10^\circ + \cos 20^\circ + ... + \cos 170^\circ + \cos 180^\circ \) bằng
\(A = \frac{3}{2}\).
\(A = 0\).
\(A = 1\).
\(A = - 1\).
Gợi ý cho bạn
Xem tất cảĐề thi Học kì 1 Toán 10 Chân trời sáng tạo có đáp án- Đề 2
Đề thi Học kì 1 Toán 10 Chân trời sáng tạo có đáp án- Đề 1
Đề thi Giữa kì 1 Toán 10 chân trời sáng tạo có đáp án - Đề 2