Đề kiểm tra Giới hạn của dãy số (có lời giải) - Đề 3
22 câu hỏi
Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.
\(\lim \frac{1}{{2n + 5}}\) bằng
\(\frac{1}{2}\).
\(0\).
\( + \infty \).
\(\frac{1}{5}\).
Tìm giới hạn \[I = \lim \frac{{3n - 2}}{{n + 3}}\].
\(I = - \frac{2}{3}\).
\(I = 1\).
\(I = 3\).
\(k \in \mathbb{Z}\).
Giới hạn \(\lim \frac{{1 - 2n}}{{3n + 1}}\) bằng?
\(\frac{2}{3}\).
\[\frac{1}{3}\].
\[1\].
\[ - \frac{2}{3}\].
Tính giới hạn \(I = \lim \frac{{2n + 2017}}{{3n + 2018}}\).
\(I = \frac{2}{3}\).
\(I = \frac{3}{2}\).
\(I = \frac{{2017}}{{2018}}\).
\(I = 1\).
\(\lim \frac{{1 + 19n}}{{18n + 19}}\) bằng
\(\frac{{19}}{{18}}\).
\(\frac{1}{{18}}\).
\( + \infty \).
\(\frac{1}{{19}}\).
Tính giới hạn \(\lim \frac{{4n + 2018}}{{2n + 1}}\).
\(\frac{1}{2}\).
\(4\).
\(2\).
\(2018\).
Tính giới hạn \(\lim \frac{{{n^2} - 3{n^3}}}{{2{n^3} + 5n - 2}}\).
\(\frac{1}{5}\).
\(0\).
\( - \frac{3}{2}\).
\(\frac{1}{2}\).
Giá trị của \(B = \lim \frac{{4{n^2} + 3n + 1}}{{{{\left( {3n - 1} \right)}^2}}}\) bằng:
\(\frac{4}{9}\).
\(\frac{4}{3}\).
\(0\).
\(4\)
Gọi S là tập hợp các tham số nguyên \[a\] thỏa mãn \[\lim \left( {\frac{{3n + 2}}{{n + 2}} + {a^2} - 4a} \right) = 0\]. Tổng các phần tử của \[S\] bằng
\(4\).
\(3\).
\(5\).
\(2\).
Cho \(a \in \mathbb{R}\) sao cho giới hạn \(\lim \frac{{a{n^2} + {a^2}n + 1}}{{{{\left( {n + 1} \right)}^2}}} = {a^2} - a + 1\).Khi đó khẳng định nào sau đây là đúng?
\(0 < a < 2\).
\(0 < a < \frac{1}{2}\).
\( - 1 < a < 0\).
\(1 < a < 3\).
Dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{\left( {3n - 1} \right){{\left( {3 - n} \right)}^2}}}{{{{\left( {4n - 5} \right)}^3}}}\) có giới hạn bằng phân số tối giản \(\frac{a}{b}\). Tính \(a.b\)
\(192\)
\(68\)
\(32\)
\(128\)
Dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{\left( {3n - 1} \right){{\left( {3 - n} \right)}^2}}}{{{{\left( {4n - 5} \right)}^3}}}\) có giới hạn bằng phân số tối giản \(\frac{a}{b}\). Tính \(a.b\)
\(192\)
\(68\)
\(32\)
\(128\)
Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Biết giới hạn \(\lim \left( { - 2{n^3} - 5n + 9} \right) = a\) và \(\lim \frac{{{4^n} + 3}}{{1 + 3 \cdot {4^{n + 1}}}} = b\). Khi đó:
a) Tích \(a.b = 3\)
b) Hàm số \(y = \sqrt {1 - x} \) có tập xác định là \(D\left( {a;1} \right]\)
c) Giá trị \(b\) là số lớn hơn \(0\)
d) Phương trình lượng giác \(\cos x = b\) vô nghiệm
Biết giới hạn và . Khi đó:
a) \(\lim \left( { - 3{n^2} + \frac{1}{n}} \right) = a\)
b) \(x = b\) là hoành độ giao điểm của đường thẳng \(y = 2x\) với trục hoành
c) \(\lim {\left( {\frac{1}{{2024}}} \right)^n} = b\)
d) Cho cấp số cộng \(\left( {{u_n}} \right)\) với công sai \(d = \frac{1}{2}\) và \({u_1} = b\), thì \({u_3} = 2\)
Tìm được tổng của cấp số nhân lùi vô hạn sau: \(S = 1 - \frac{1}{2} + \frac{1}{4} - \frac{1}{8} + \ldots \) và \(T = 1 + \frac{1}{3} + \frac{1}{{{3^2}}} + \ldots + \frac{1}{{{3^n}}} + \ldots \)Khi đó:
a) \(1 - \frac{1}{2} + \frac{1}{4} - \frac{1}{8} + \ldots \)là tổng của cấp số nhân lùi vô hạn có công bội \(q = - \frac{1}{2}.\)
b) \(1 + \frac{1}{3} + \frac{1}{{{3^2}}} + \ldots + \frac{1}{{{3^n}}} + \ldots \)là tổng của cấp số nhân lùi vô hạn có công bội \(q = \frac{1}{3}{\rm{. }}\)
a) \(S > T\)
b) \(S = \frac{1}{T}\)
Cho \({u_n} = \frac{{{7^n} + {2^{2n - 1}} + {3^{n + 1}}}}{{{7^{n + 1}} + {5^{n - 1}}}}\). Biết \(\lim {u_n} = \frac{a}{b}\) (với \(a,b \in \mathbb{Z};\frac{a}{b}\) tối giản). Khi đó:
a) \(a + b = 8\)
b) \(a - b = - 7\)
c) Bộ ba số \(a;b;13\) tạo thành một cấp số cộng có công sai \(d = 7\)
d) Bộ ba số \(a;b;49\)tạo thành một cấp số nhân có công bội \(q = 7\)
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Tính \(\mathop {\lim }\limits_{n \to + \infty } \left( {{n^2} - n + 3} \right)\).
Cho dãy số \(\left( {{u_n}} \right)\) có tính chất \(\left| {{u_n} - \frac{n}{{n + 1}}} \right| \le \frac{1}{{{n^2}}}\). Tính \(\mathop {\lim }\limits_{n \to + \infty } {u_n}\).
Tính tổng \(M = \frac{1}{5} + \frac{1}{{{5^2}}} + \frac{1}{{{5^3}}} + ... + \frac{1}{{{5^{10}}}}\)
Cho tổng: \({S_n} = \frac{1}{{1.2.3}} + \frac{1}{{2.3.4}} + \frac{1}{{3.4.5}} + ... + \frac{1}{{n\left( {n + 1} \right)\left( {n + 2} \right)}}\). Tính \[{S_{30}}\]
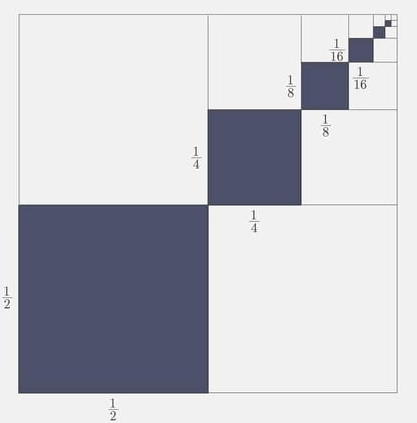
Để trang hoàng cho căn hộ của mình, chú chuột Mickey quyết định tô màu một miếng bìa hình vuông cạnh bằng 1. Nó tô màu xám các hình vuông nhỏ được đánh số lần lượt là 1, 2, 3, 4, …n,… trong đó cạnh của hình vuông kế tiếp bằng một nửa cạnh hình vuông trước đó.Giả sử quy trình tô màu của chuột Mickey có thể tiến ra vô hạn (như hình vẽ dưới đây). Tính tổng diện tích mà chuột Mickey phải tô màu.
Từ độ cao 63m của tháp nghiêng Pi-sa ở Italia, người ta thả một quả bóng cao su xuống đất. Giả sử mỗi lần chạm quả bóng lại nảy lên độ cao bằng \(\frac{1}{{10}}\) độ cao mà quả bóng đạt được ngay trước đó. Tính độ dài hành trình của quả bóng từ thời điểm ban đầu cho đến khi nó nằm yên trên mặt đất.








