Đề kiểm tra Giá trị lớn nhất và giá trị nhỏ nhất của hàm số (có lời giải) - Đề 5
24 câu hỏi
Cho hàm số \(y = \frac{{{x^2} + 4}}{x}\), khi đó giá trị nhỏ nhất của hàm số trên khoảng \(\left( {0; + \infty } \right)\)đạt được tại điểm nào?
\(x = 1\).
\(x = 4\).
\(x = 3\).
\(x = 2\).
Giá trị lớn nhất hàm sô \(y = {x^4} - 4{x^2} + 5\)trên \(\left[ { - 2;3} \right]\)là:
\(122\).
\(1\).
\(5\).
\(50\).
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1\,;\,3} \right]\) và có đồ thị như hình vẽ. Giá trị lớn nhất của hàm số đã cho trên đoạn \(\left[ { - 1\,;\,3} \right]\) bằng![Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1\,;\,3} \right]\) và có đồ thị như hình vẽ. Giá trị lớn nhất của hàm số đã cho trên đoạn \(\left[ { - 1\,;\,3} \right]\) bằng A. \[3\]. B. \[2\]. C. \[0\]. D. \[1\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/14-1759149666.png)
\[3\].
\[2\].
\[0\].
\[1\].
Cho hàm số \(y = f(x)\) xác định và liên tục trên \(\mathbb{R}\) có đồ thị bên dưới. Gọi \[M,{\rm{ }}m\] lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn \[[1;3].\] Giá trị của \[M + m\] bằng:![Giá trị của \[M + m\] bằng: (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/15-1759149709.png)
\(M + m = 2\).
\(M + m = - 4\).
\(M + m = - 3\).
\(M + m = 1\).
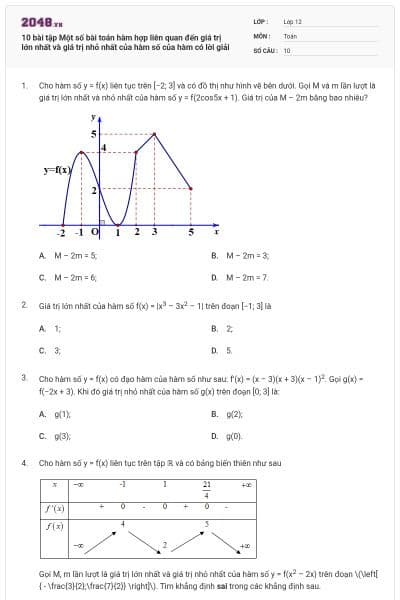
Cho hàm số \[y = f(x)\] liên tục trên \[[ - 2;3]\] và có đồ thị như hình vẽ bên dưới. Gọi \[M\] và \[m\]lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số \[y = f({\rm{2cos}}\,5x + 1).\] Giá trị của \[M - 2m\]bằng bao nhiêu?![Giá trị của \[M - 2m\] bằng bao nhiêu? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/16-1759149760.png)
\(M - 2m = 5\).
\(M - 2m = 3\).
\(M - 2m = 6\).
\(M - 2m = 7\).
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right)\) tại mọi \(x \in \mathbb{R}\). Đồ thị của hàm số \(y = f'\left( x \right)\) được cho như hình vẽ dưới đây.
![. Biết rằng \(f\left( 0 \right) + f\left( 3 \right) = f\left( 2 \right) + f\left( 5 \right)\). Hãy tìm giá trị nhỏ nhất, giá trị lớn nhất của \(y = f\left( x \right)\) trên đoạn \(\left[ {0;5} \right]\)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/17-1759149805.png)
Biết rằng \(f\left( 0 \right) + f\left( 3 \right) = f\left( 2 \right) + f\left( 5 \right)\). Hãy tìm giá trị nhỏ nhất, giá trị lớn nhất của \(y = f\left( x \right)\) trên đoạn \(\left[ {0;5} \right]\)?
\(\mathop {Max}\limits_{\left[ {0;5} \right]} f\left( x \right) = f\left( 5 \right)\).
\(\mathop {Max}\limits_{\left[ {0;5} \right]} f\left( x \right) = f\left( 0 \right)\).
\(\mathop {Max}\limits_{\left[ {0;5} \right]} f\left( x \right) = f\left( 2 \right)\).
\(\mathop {Max}\limits_{\left[ {0;5} \right]} f\left( x \right) = f\left( 3 \right)\).
Cho hàm số \[y = f\left( x \right)\] liên tục trên R và có bảng biến thiên như hình dưới đây
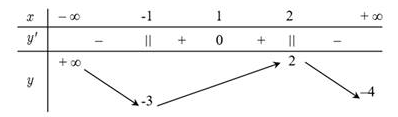
Trong các mệnh đề sau, mệnh đề nào sai?
Giá trị lớn nhất của hàm số \[y = f\left( x \right)\] trên đoạn \(\left[ { - 1;\,2} \right]\) bằng 2.
Giá trị nhỏ nhất của hàm số \[y = f\left( x \right)\] trên đoạn \(\left[ { - 1;\,2} \right]\) bằng -3.
Giá trị nhỏ nhất của hàm số\[y = f\left( x \right)\] trên nửa khoảng \(\left[ { - 1;\, + \infty } \right)\) bằng -4.
Giá trị lớn nhất của hàm số \[y = f\left( x \right)\] trên nửa khoảng \(\left[ { - 1;\, + \infty } \right)\) bằng 2.
Cho hàm số \[y = f\left( x \right)\] liên tục trên \[\left[ { - 3;2} \right]\] và có bảng biến thiên như hình dưới đây. Gọi \[M,\,m\] lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \[y = f\left( x \right)\] trên đoạn \[\left[ { - 1;\,2} \right]\]. Tính \[2M + 3m\].![Cho hàm số \[y = f\left( x \right)\] liên tục trên \[\left[ { - 3;2} \right]\] và có bảng biến thiên như hình dưới đây. Gọ (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/20-1759149944.png)
\(0\).
\(6\).
\( - 2\).
\(8\).
Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên R, có đồ thị trên đoạn\(\left[ { - 1;\,3} \right]\) như hình vẽ dưới đây.![Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên R, có đồ thị trên đoạn\(\left[ { - 1;\,3} \right]\) như hình vẽ dưới đây. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/21-1759150014.png)
Tìm giá trị lớn nhất \(M\)của hàm số \(y = g\left( x \right) = f\left( {\sin x + 1} \right)\) trên tập \(\mathbb{R}\).
\(M = 3\).
\(M = 0\).
\(M = 1\).
\(M = 2\).
Giá trị lớn nhất của hàm số \(f\left( x \right) = \left| {{x^3} - 3{x^2} - 1} \right|\) trên đoạn \(\left[ { - \,1;3} \right]\) là
\(1\).
\(3\).
\(2\).
\[5\].
Cho hàm số \(y = {x^3} - 3x + m\). Giá trị của tham số \(m\) để giá trị nhỏ nhất của hàm số trên đoạn \(\left[ {0;2} \right]\) bằng \(1\) là
\(m = 1\).
\(m = 3\).
\(m = - \,1\).
\(m = 2\).
Cho hàm số \(f\left( x \right) = \frac{{x + {m^2}}}{{x - 1}}\). Tất cả các giá trị của tham số \(m\) để hàm số \(f\left( x \right)\) có giá trị nhỏ nhất trên đoạn \(\left[ { - \,2;0} \right]\) lớn hơn \( - \,4\) là
\(\left[ \begin{array}{l}m > 2\\m < - \,2\end{array} \right.\).
\( - \,2 < m < 2\).
\( - \,\sqrt {14} < m < \sqrt {14} \).
\(\left[ \begin{array}{l}m > \sqrt {14} \\m < - \,\sqrt {14} \end{array} \right.\).
Gọi \(S\) là tập hợp tất cả các giá trị thực của tham số \(m\) sao cho giá trị lớn nhất của hàm số \(y = \left| {\frac{{{x^2} + mx + m}}{{x + 1}}} \right|\) trên \(\left[ {1;2} \right]\) bằng \(2\). Số phần tử của tập \(S\) là
\[1\].
\[2\].
\[3\].
\[4\].
Cho một tấm nhôm hình chữ nhật có kích thước \[15\,{\rm{cm}} \times 24\,{\rm{cm}}\]. Người ta cắt bỏ 4 góc của tâm tôn 4 miếng hình vuông bằng nhau rồi gò lại thành một hình hộp chữ nhật không có nắp. Để thể tích của hình hộp đó lớn nhất thì độ dài cạnh hình vuông của các miếng tôn bị cắt bỏ bằng
\[3\,{\rm{cm}}\].
\[4\,{\rm{cm}}\].
\[5\,{\rm{cm}}\].
\[2\,{\rm{cm}}\].
Trong các khẳng định sau, khẳng định nào đúng hay sai?
Khẳng định | Đúng | Sai | |
a) | Giá trị nhỏ nhất của hàm số \(y = 2{x^3} + 3{x^2} - 1\) trên đoạn \(\left[ { - 2;1} \right]\) là \( - 5\). |
|
|
b) | Hàm số \(y = 4{x^3} - 12{x^2} + 9x\) đạt giá trị lớn nhất trên đoạn \(\left[ {0;1} \right]\) tại điểm \(x = 2\). |
|
|
c) | Giá trị nhỏ nhất của hàm số \(y = \sqrt {4x - {x^2}} \) là \(4\). |
|
|
d) | Hàm số \(y = x + \frac{4}{x}\) không có giá trị lớn nhất trên khoảng \(\left( {0; + \infty } \right)\). |
|
|
Cho hàm số \(y = f\left( x \right)\)có đạo hàm của của số như sau:\(f'\left( x \right) = \left( {x - 3} \right)\left( {x + 3} \right){\left( {x - 1} \right)^2}\).
Trong các khẳng định sau, khẳng định nào đúng hay sai?
Khẳng định | Đúng | Sai | |
a)[1] | Giá trị lớn nhất của hàm số trên đoạn \(\left[ { - 3;3} \right]\) là \(f\left( { - 3} \right)\). |
|
|
b)[1] | Hàm số có giá trị lớn nhất trên \(\mathbb{R}\). |
|
|
c)[2] | Gọi \[g\left( x \right) = f\left( { - 2x + 3} \right)\]. Khi đó giá trị nhỏ nhất của hàm số \(g\left( x \right)\) trên đoạn \(\left[ {0;3} \right]\) là \(g\left( 3 \right)\). |
|
|
d)[3] | Gọi \[h\left( x \right) = f\left( { - x + 5} \right)\]và \[h\left( 0 \right) + h\left( 4 \right) = h\left( 2 \right) + h\left( 8 \right)\]. Giá trị lớn nhất của hàm số \(h\left( x \right)\) trên đoạn \(\left[ {0;8} \right]\) là \(h\left( 8 \right)\). |
|
|
Cho hàm số \(y = f\left( x \right) = {x^3} - 3{x^2} - 9x + 7\).
Trong các khẳng định sau, khẳng định nào đúng hay sai?
Khẳng định | Đúng | Sai | |
a)[1] | Giá trị lớn nhất của hàm số\(y = f\left( x \right)\) trên đoạn \(\left[ { - 2;0} \right]\) là \(12\). |
|
|
b)[2] | Hàm số\(y = f\left( x \right) + m\) đạt giá trị nhỏ nhất trên đoạn \(\left[ { - 2;0} \right]\) là \(10\) khi \(m = 3\). |
|
|
c)[3] | Giá trị nhỏ nhất của hàm số \(y = f(2{x^2} + 1) - 5\)là \( - 25\). |
|
|
d)[3] | Hàm số \(y = \left| {f(x) + m} \right|\) đạt giá trị nhỏ nhất trên đoạn \(\left[ {0;4} \right]\) là \(17\) có tích các giá trị của m là . |
|
|
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\mathbb{R}\) và có đồ thị như hình vẽ.
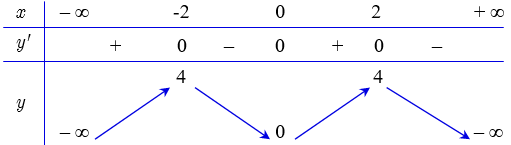
Trong các khẳng định sau, khẳng định nào đúng hay sai?
Khẳng định | Đúng | Sai | |
a)[1] | \(\mathop {\max }\limits_{{\rm{[}}0;2]} f(x) = 4\). |
|
|
b)[1] | Hàm số \(y = f\left( x \right)\) có giá trị lớn nhất là 4 và giá trị nhỏ nhất là 0. |
|
|
c)[2] | Hàm số \(y = f\left( {2\cos x} \right)\) có giá trị lớn nhất là 4 tại \(x = \frac{\pi }{2}\).
|
|
|
d)[3] | Không tồn tại giá trị lớn nhất của hàm số \(y = f\left( {f(x)} \right)\) trên \(\left( { - 2;2} \right)\). |
|
|
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 20 đến câu 25.
Tìm giá trị nhỏ nhất của hàm số \(y = {x^3} - 3x + 4\) trên đoạn \(\left[ {0;2} \right]\)
Cho hàm số \(y = f(x)\) liên tục và có bảng biến thiên trên đoạn \(\left[ { - 1\,;\,3} \right]\) như hình vẽ bên. Giả sử giá trị lớn nhất của \(y = f(x)\)trên \(\left[ { - 1\,;\,3} \right]\)đạt được tại giá trị x0. Tìm x0
![Cho hàm số \(y = f(x)\) liên tục và có bảng biến thiên trên đoạn \(\left[ { - 1\,;\,3} \right]\) như hình vẽ bên. Giả sử giá trị lớn nhất của \(y = f(x)\)trên \(\left[ { - 1\,;\,3} \right]\)đạt được tại giá trị x0. Tìm x0 (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/9-1759150879.png)
Cho hàm số có \(f\left( x \right)\) có đạo hàm là hàm \(f'\left( x \right)\). Đồ thị hàm số \(f'\left( x \right)\) như hình vẽ bên. Biết rằng \(f\left( 0 \right) - f\left( 2 \right) = f\left( 4 \right) - f\left( 3 \right)\). Giả sử giá trị nhỏ nhất \(m\) và giá trị lớn nhất \(M\) của \(f\left( x \right)\) trên đoạn \(\left[ {0;4} \right]\)đạt được lần lượt tại \({x_0}\)và\({x_1}\). Tìm\({x_0}\)và\({x_1}\).![Giả sử giá trị nhỏ nhất \(m\) và giá trị lớn nhất \(M\) của \(f\left( x \right)\) trên đoạn \(\left[ {0;4} \right]\)đạt được lần lượt tại \({x_0}\)và\({x_1}\). Tìm\({x_0}\)và\({x_1}\). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/screenshot-3628-1759151183.png)
Gọi S là tập hợp chứa các tham số \(m\) để đồ thị hàm số \(y = \frac{{mx - 1}}{{x + m}}\) có tiệm cận đứng và tiệm cận ngang tạo với các trục tọa độ hình chữ nhật có diện tích bằng 4. Số phần tử của S là
Giả sử số lượng của một quần thể nấm men tại môi trường nuôi cấy trong phòng thí nghiệm được mô hinh hoá bằng hàm số \(P(t) = \frac{a}{{b + {e^{ - 0,75t}}}}\), trong đó thời gian \(t\) được tính bằng giờ. Tại thời điểm ban đầu \(t = 0\), quần thể có 20 tế bào và tăng với tốc độ 12 tế bào/giờ. Tìm các giá trị của \(a\) và \(b\). Theo mô hình này, số lượng nấm men không vượt quá bao nhiêu?
Cho hàm số \(y = f\left( x \right)\) là hàm đa thức bậc hai và có đồ thị hàm số \(f\left( {{x^2} - 1} \right)\) như hình vẽ.
![Đặt \[g\left( x \right) = \left| {f\left( {{x^2}} \right) + m} \right|\]. Có bao nhiêu giá trị nguyên thuộc [-2024;2024] của tham số m để với mọi bộ ba số phân biệt (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/10-1759151329.png)
Đặt \[g\left( x \right) = \left| {f\left( {{x^2}} \right) + m} \right|\]. Có bao nhiêu giá trị nguyên thuộc [-2024;2024] của tham số m để với mọi bộ ba số phân biệt \[a,b,c\] thuộc [-2;2] ta đều có bộ ba số \[g\left( a \right);g\left( b \right);g\left( c \right)\]là số đo độ dài ba cạnh của một tam giác?